The document is a set of lecture notes on complex numbers, outlining their definition, arithmetic operations, properties, and geometric representation in the complex plane. It discusses complex conjugates, modulus, and argument as well as their applications in equations and geometry. Key concepts include addition, subtraction, multiplication, and division of complex numbers, along with transformations to polar form and the relationship between these forms.

1. MT1002 Mathematics
Complex Numbers Lecture Notes
Tom Coleman
Room 218
tdhc@st-andrews.ac.uk
Spring 2019
1 / 44

2. 1: What’s going on?
Common problems in mathematics, science and the humanities can
be boiled down to equations like y = 3x2 − 2. Often, questions are
asked like ‘given a value for y, what value for x will give us this y
when put into the equation above?’ For instance, the values of x
that give 10 = 3x2 − 2 are x = ±2. There are some equations that
can’t be solved using real numbers. For instance, what values of x
satisfy the equation
x2
+ 1 = 0
There is no real number that when multiplied by itself gives a
negative number.
Complex numbers extend the number system by including a
symbol i =
√
−1. Any equation like the ones above has at least
one solution in the complex numbers.
2 / 44

3. Complex numbers
Definition 1.1 (complex number, real and imaginary parts)
I A complex number is an expression of the form z = a + bi,
where a and b are real numbers and i =
√
−1.
I For a complex number z = a + bi, say that Re(z) = a is the
real part of z, and Im(z) = b is the imaginary part of z.
I A complex number z = a + bi is called real if Im(z) = b = 0,
and purely imaginary if Re(z) = a = 0.
I Two complex numbers z = a + bi and w = c + di are equal if
and only both their real and imaginary parts are equal; that is,
when both a = c and b = d.
Definition 1.2 (complex conjugate)
The complex conjugate of z = a + bi is defined to be the
complex number z̄ = a − bi.
3 / 44

4. Example 1.3
I Let z1 = 7 − 6i. Then Re(z1) = 7, Im(z1) = −6 and
z̄1 = 7 + 6i.
I Let z2 = 18i = 0 + 18i. Then Re(z2) = 0 (so z2 is purely
imaginary), Im(z2) = 18 and z̄2 = 0 − 18i = −18i.
I Let z3 = 2 = 2 + 0i. Then Re(z3) = 2, Im(z3) = 0 (so z3 is
real), and z̄3 = 2 − 0i = 2.
4 / 44

5. Complex arithmetic 1
Arithmetic on numbers – adding, subtracting, multiplication and
division – enables you to solve everyday problems. If the problem
involves complex numbers, you need to be able to do arithmetic on
complex numbers.
Arithmetic on complex numbers is based on the same rules of
algebra that you have learned in your previous education, together
with the key feature that
i2
= i · i =
√
−1 ·
√
−1 = −1.
(It also follows that
i3
= i2
· i = (−1) · i = −i and i4
= i2
· i2
= (−1) · (−1) = 1.
Similarly, (−i)2 = (−1)2 · i2 = 1 · (−1) = −1.)
5 / 44

6. Complex arithmetic 2 (adding, subtracting, multiplying)
Let z = a + bi and w = c + di. Then the following are defined:
z + w = (a + bi) + (c + di) = (a + c) + (b + d)i
z − w = (a + bi) − (c + di) = (a − c) + (b − d)i
zw = (a + bi)(c + di)
= ac + bci + adi + bdi2
= (ac − bd) + (bc + ad)i
6 / 44

7. Example 1.4
Let z = 3 − 4i and w = −2 + 2i. Then
z + w = (3 − 4i) + (−2 + 2i)
= (3 + (−2)) + ((−4) + 2)i = 1 − 2i
z − w = (3 − 4i) − (−2 + 2i)
= (3 − (−2)) + ((−4) − 2)i = 5 − 6i
zw = (3 − 4i)(−2 + 2i)
= 3(−2) + (3)(2i) + (−4)(−2i) + (−4)(2)i2
= −6 + 8i + 6i + 8 = 2 + 14i
7 / 44

8. Complex arithmetic 3 (dividing)
Division is slightly different. How can you express
z/w = (a + bi)/(c + di) in the form x + yi?
The way to do this is by using complex conjugates. If z = a + bi,
then z̄ = a − bi and
zz̄ = (a + bi)(a − bi) = a2
− abi + abi − b2
i2
= a2
+ b2
which is a real number; you can divide by real numbers!
So multiplying top and bottom of z/w by w̄ gives
z
w
=
zw̄
ww̄
=
(a + bi)(c − di)
(c + di)(c − di)
=
(ac + bd) + (bc − ad)i
c2 + d2
(Don’t try and remember this formula; learn the technique!)
8 / 44

9. Example 1.5
Once again, let z = 3 − 4i and w = −2 + 2i. What is z/w?
The complex conjugate of w is w̄ = −2 − 2i. Multiplying top and
bottom of z/w by w̄ and simplifying gives
z
w
=
3 − 4i
−2 + 2i
=
(3 − 4i)(−2 − 2i)
(−2 + 2i)(−2 − 2i)
=
−6 − 6i + 8i + 8i2
4 − 4i + 4i − 4i2
=
−14 + 2i
8
= −
7
4
+
i
4
9 / 44

10. Rules of complex arithmetic
The usual rules of arithmetic apply to complex numbers. For
instance, if z1, z2 and z3 are complex numbers, then
I (z1 + z2) + z3 = z1 + (z2 + z3) and (z1z2)z3 = z1(z2z3)
(associativity)
I z1 + z2 = z2 + z1 and z1z2 = z2z1 (commutativity)
I z1(z2 + z3) = z1z2 + z1z3 (distributivity)
Exercise: Show the complex numbers are commutative.
10 / 44

11. Properties of the complex conjugate
Proposition 1.6
For a complex number z = a + bi and its conjugate z̄ = a − bi,
then the following properties hold:
I Re(z̄) = Re(z) and Im(z̄) = −Im(z).
I If z is real, then z̄ = z. If z is purely imaginary, then z̄ = −z.
I z + z̄ = 2Re(z) = 2a and z − z̄ = 2Im(z)i = 2bi.
I zz̄ = a2 + b2 (see slide: Complex arithmetic 3).
I ¯
z̄ = z.
Exercise: Prove that these properties are true.
11 / 44

12. 2: The complex plane (Argand diagram)
A complex number z = a + bi can be translated to the point (a, b)
in the standard Cartesian co-ordinate system, and vice versa; every
point (a, b) represents a complex number z.
This picture is called the complex plane or an Argand diagram.
On this picture, the x-axis is called the real axis (as it represents
the real part of a complex number) and the y-axis is called the
imaginary axis.
12 / 44

13. Example 1.7
Re
Im
−4
−3
−2
−1
1
2
3
4
1 2 3 4 5
−1
−2
−3
−4
−5
z = 3 + 2i
w = −2 + 4i
u = 0 − 3i
v = −5 + 0i
z̄ = 3 − 2i
13 / 44

14. Modulus and argument
You can also think of the complex number z = a + bi as the vector
from (0, 0) to the point (a, b) in the plane.
arg z
|z|
z = a + bi
Re
Im
b
a
I The length |z| of this vector
is called the modulus of z.
This is always a positive real
number.
I The angle θ (always in
radians) this vector makes
with the positive x-axis
(taken anticlockwise) is
called the argument of z
and is written arg z.
14 / 44

15. Finding the modulus
You can use Pythagoras’ Theorem to find the modulus of
z = a + bi.
|z|
b
z
Re
Im
a
I Here, |z| is the hypotenuse of the
right-angled triangle with shorter
sides of length a and b.
I So |z|2 = a2 + b2, giving
|z| =
√
a2 + b2.
15 / 44

16. Finding the argument
You can work out arg z = θ by trigonometry; it is a solution to the
equations
cos θ =
a
|z|
=
Re(z)
|z|
and sin θ =
b
|z|
=
Im(z)
|z|
There is a unique solution to these equations between −π and π;
this solution θ is called the principal argument Arg z of z.
The principal argument Arg z = θ is not the only angle that
satisfies the equations above. There are infinitely many angles that
do; they are of the form Arg z + 2kπ for k ∈ Z. Any argument
arg z of z is in this set of numbers.
16 / 44

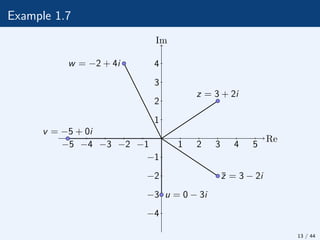
17. Example 1.8
Let z = 1 + i
√
3. Here, the modulus of z is
|z| =
q
12 + (
√
3)2 =
√
1 + 3 = 2
θ
|z|
z
Re
Im
√
3
1
I Here, the principal argument
Arg(z) is the unique solution
θ ∈ (−π, π] to the equations
cos θ = a/|z| and sin θ = b/|z|.
I So cos θ = 1/2 and sin θ =
√
3/2.
I The unique solution to these
equations between −π and π is
π/3. So Arg z = π/3.
It’s possible that arg z = 7π/3, or arg z = −5π/3. These
arguments are not principal!
17 / 44

18. Distance between two complex numbers
Let z = a + bi and w = c + di be two complex numbers.
|z − w|
z
w
Re
Im
b
d
a c
I Here, |z − w| = |(a − c) + (b − d)i|
and so by definition of modulus,
|z − w| =
q
(a − c)2 + (b − d)2.
I By Pythagoras’ theorem, this is
precisely the distance between the
two points (a, b) and (c, d) in the
plane.
So |z − w| represents the distance between the two complex
numbers z and w. You can then use this notation to describe
shapes and lines in the complex plane.
18 / 44

19. Curves in the complex plane 1
Let z, w, v be complex numbers and c > 0 be a real number.
I The solutions z of |z − w| = c are all those complex numbers
z at a distance c from w. Geometrically, this is a circle in the
complex plane with centre w and radius c.
I The solutions z of |z − w| = |z − v| are all those complex
numbers that are equidistant from both v and w.
Geometrically, this is the perpendicular bisector of the
complex numbers u and v in the complex plane.
I The solutions z of |z − w| + |z − v| = c are all those complex
numbers z whose distances between v and w add up to c.
Geometrically, this is an ellipse in the complex plane with foci
v and w, and major axis length of c.
19 / 44

20. Curves in the complex plane 2
Let z, w be complex numbers and c, θ be real numbers with
θ ∈ (−π, π].
There are two more cases to watch out for:
I The solutions z of Re(z − w) = c are all those complex
numbers with real part c + Re(w). In the complex plane, this
is a vertical line through the point c + Re(w) on the real axis.
Similarly, solutions z of Im(z − w) = c are all those complex
numbers with imaginary part c + Im(w); geometrically, this is
a horizontal line through the point (c + Im(w))i on the
imaginary axis.
I The solutions z of Arg(z − c) = θ are all those complex
numbers with principal argument θ if c was viewed as the
origin. In the complex plane, this corresponds to a line
starting at c, at an angle of θ from the real axis.
20 / 44

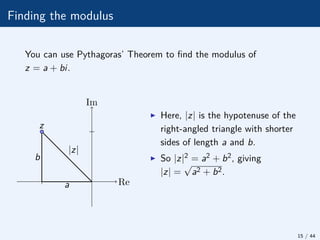
21. 3: Polar form of a complex number
Any complex number z = a + bi can be described uniquely by its
modulus |z| and its principal argument Arg z = θ ∈ (−π, π]. This
gives another way to write z which can be very convenient.
θ
r
z = a + bi
Re
Im
b
a
I In the diagram, Pythagoras’
theorem implies that
r = |z| =
√
a2 + b2.
I Trigonometry implies that
cos θ = a/r and sin θ = b/r,
and so r cos θ = a and
r sin θ = b.
So z = a + bi = r cos θ + ir sin θ = r(cos θ + i sin θ)
This is the modulus-argument or polar form of a complex
number z. 21 / 44

22. Example 1.9
Let z = −1 + i
√
3. The modulus of z is
|z| =
q
(−1)2 + (
√
3)2 =
√
1 + 3 = 2
θ
|z|
z
Re
Im
√
3
−1
I The principal argument Arg(z) is
the unique solution θ ∈ (−π, π] to
the equations cos θ = a/|z| and
sin θ = b/|z|.
I So cos θ = −1/2 and sin θ =
√
3/2.
I The unique solution to these
equations between −π and π is
2π/3. So Arg z = 2π/3.
So you can write z in polar form as z = 2(cos(2π/3) + i sin(2π/3)).
22 / 44

23. Example 1.10
Let z = 3 − 3i. The modulus of z is
|z| =
q
(3)2 + (3)2 =
√
2 · 9 = 3
√
2
θ
|z|
z
Re
Im
−3
3
I The principal argument Arg(z) is
the unique solution θ ∈ (−π, π] to
the equations
cos θ = a/|z| = 3/3
√
2 and
sin θ = b/|z| = −3/3
√
2.
I So cos θ = 1/
√
2 and
sin θ = −1/
√
2.
The solution to these equations between −π and π is −π/4. So
Arg z = −π/4, giving z = 3
√
2(cos(−π/4) + i sin(−π/4)).
(The minus sign in Arg z tells you to turn clockwise from the
positive real axis.) 23 / 44

24. Multiplication in polar form
It may seem overblown to write complex numbers in polar form,
but it can be very useful! Complex multiplication (and
exponentiation, see slide: Powers) can become easier to do.
Proposition 1.11
For two complex numbers z1z2, the following results hold:
I |z1z2| = |z1| · |z2|
I arg(z1z2) = arg(z1) + arg(z2).
You can prove this using trigonometric sum identities. By using
proof by induction (from later in the course), you can prove this
statement for any length of product of complex numbers.
24 / 44

25. Example 1.12
From Example 1.8, it follows that
z = 1 + i
√
3 = 2(cos(π/3) + i sin(π/3))
Set w = 3 − 3i, so w = 3
√
2(cos(−π/4) + i sin(−π/4)) (from
Example 1.10)
Using Proposition 1.11, it follows that
zw = (1 + i
√
3)(3 − 3i)
= (2 · 3
√
2)(cos(π/3 + (−π/4)) + i sin(π/3 + (−π/4)))
= 6
√
2(cos(π/12) + i sin(π/12))
25 / 44

26. 4: Powers of complex numbers
You’ve seen in the previous proposition that |z1z2| = |z1| · |z2| for
any two complex numbers. In addition,
arg(z1z2) = arg(z1) + arg(z2).
You can apply this to z2. Here,
|z2
| = |z||z| = |z|2
and arg(z2
) = arg(z) + arg(z) = 2 arg(z)
Similarly,
|z3
| = |z2
||z| = |z|3
and arg(z3
) = arg(z2
) + arg(z) = 3 arg(z)
You can do this as many times as you wish! So for any positive
integer n:
|zn
| = |z|n
and arg(zn
) = n arg(z) (†)
26 / 44

27. Negative powers of complex numbers
This idea of complex exponentiation can be extended to negative
integers. Suppose that n is a positive integer and that z 6= 0 is a
complex number. Since zn · z−n = 1, you can write
1 = |zn
z−n
| = |zn
||z−n
| = |z|n
|z−n
|
and dividing both sides of this equation by |z|n gives |z−n| = |z|−n.
Similarly,
arg 1 = 0 = arg(zn
z−n
) = arg(zn
)+arg(z−n
) = n arg(z)+arg(z−n
)
Rearranging gives
arg(z−n
) = −n arg(z)
So (†) holds for all integers z.
27 / 44

28. de Moivre’s theorem
If z = cos θ + i sin θ then arg(zn) = nθ for all integers n (see above
working). This gives:
Theorem 1.13 (de Moivre’s theorem)
(cos θ + i sin θ)n = cos(nθ) + i sin(nθ)
If z = r(cos θ + i sin θ), then applying (†) gives
(r(cos θ + i sin θ))n
= rn
(cos θ + i sin θ) (∆)
28 / 44

29. Example 1.14
What is (1 + i
√
3)9? You know that from Example 1.12 that
(1 + i
√
3) = 2(cos(π/3) + i sin(π/3))
So using de Moivre’s theorem (∆), you can write that
(1 + i)9
= 2(cos(π/3) + i sin(π/3))
= (2(cos(π/3) + i sin(π/3)))9
= 29
(cos(9 · π/3) + i sin(9 · π/3))
= 29
(cos(3π) + i sin(3π))
= 29
(−1 + 0) = −29
= −512
29 / 44

30. Multiple angle formulas
In MT1001 or your schooling, you saw the double-angle formulas
cos(2θ) = cos2
θ − sin2
θ and sin(2θ) = 2 sin θ cos θ
de Moivre’s theorem can be used to write down some n-tuple angle
formulas, for any positive integer n. For example, you can use de
Moivre’s theorem to say that
cos(3θ) + i sin(3θ) = (cos θ + i sin θ)3
Expanding the brackets on the right hand side, equating real and
imaginary parts of both sides, and using cos2 θ + sin2
θ gives the
triple-angle formulas
cos(3θ) = 4 cos3
θ − 3 cos θ and sin(3θ) = 3 sin θ − 4 sin3
θ
30 / 44

31. 5: How do you solve a problem like zn
= w? (1/2)
Let z and w be complex numbers, and let n be a positive integer.
Up to now, it has been difficult or even impossible to find solutions
to the equation zn = w. de Moivre’s theorem gives us the power
(no pun intended) to do this.
Let w = r(cos θ + i sin θ) and z = ρ(cos φ + i sin φ). From (∆),
and the fact that zn = w, you can write
ρn
(cos(nφ) + i sin(nφ)) = r(cos(θ) + i sin(θ))
This happens if and only if ρn = r (and so r1/n = ρ),
cos(θ) = cos(nφ) and sin(θ) = sin(nφ).
31 / 44

32. How do you solve a problem like zn
= w? (2/2)
In this case, nφ does not have to equal θ; it could be θ + 2π,
θ + 4π, and so on. Due to the periodicity of cos and sin, these all
give the same complex number. So nφ = θ + 2πk for some integer
k, giving φ = (θ + 2πk)/n. Therefore
z = r1/n
cos
θ + 2πk
n
+ i sin
θ + 2πk
n
There are n distinct solutions for k = 0, 1, . . . , n − 1. (Setting
k = n gives θ/n + 2π; this argument gives the same complex
number as when k = 0.)
These are all possible solutions for zn = w.
32 / 44

33. A step-by-step guide to finding nth roots z of w (1/2)
Step 1: Find the modulus and principal argument for the complex
number w. Using these, write down an expression for the
argument of w in the form arg w = Arg w + 2kπ, where k
is any integer.
Step 2: Write zn = |w| (cos(arg w) + i sin(arg w)). By de Moivre’s
theorem, it follows that
z = |w|1/n
cos
Arg w + 2kπ
n
+ i sin
Arg w + 2kπ
n
Simplify the best you can.
33 / 44

34. A step-by-step guide to finding nth roots z of w (2/2)
Step 3: The nth root z of w depends on your choice of k. The values
k = 0, 1, . . . , n − 1 give all the distinct nth roots of w. Write
down an expression for all possible roots zk. In your answers,
your choice of θ does not have to be a principal argument.
Change to the form a + bi if possible.
Step 4: Draw all roots zk on an Argand diagram.
34 / 44

35. Example 1.15 (1/3)
Solve z5 = i. Here, the modulus of i is 1 and the principal
argument is π/2. Therefore, arg i = π/2 + 2kπ, where k ∈ Z. This
means that
zn = 1 · (cos(π/2 + 2kπ) + sin(π/2 + 2kπ))
and so, by de Moivre’s theorem
z = 11/5
cos
π/2 + 2kπ
5
+ i sin
π/2 + 2kπ
5
=
cos
π
10
+
2kπ
5
+ i sin
π
10
+
2kπ
5
As n = 5 in this case, the values k = 0, 1, 2, 3, 4 give distinct
solutions to z5 = i.
35 / 44

36. Example 1.15 (2/3)
The 5 distinct solutions to z5 = i are:
zn = 1 · (cos(π/2 + 2kπ) + sin(π/2 + 2kπ))
and so, by de Moivre’s theorem
z0 = (cos (π/10) + i sin (π/10))
z1 = (cos (π/2) + i sin (π/2)) = i
z2 = (cos (9π/10) + i sin (9π/10))
z3 = (cos (13π/10) + i sin (13π/10))
z4 = (cos (17π/10) + i sin (17π/10))
An Argand diagram is given on the next page.
36 / 44

37. Example 1.15 (3/3)
Re
Im
z0
z1
z2
z3
z4
Figure: Argand diagram for all values of (i)1/5
37 / 44

38. 6: Euler’s formula (1/2)
There’s a shorter way to write complex numbers in polar form, as
well as perform exponentiation in the complex numbers. This will
come from the exponential function.
For x a real number, the power series for cos x and sin x are
cos x = 1 −
x2
2!
+
x4
4!
−
x6
6!
+
x8
8!
− . . .
sin x = x −
x3
3!
+
x5
5!
−
x7
7!
+
x9
9!
− . . .
and the power series for ex is
ex
= 1 + x +
x2
2!
+
x3
3!
+
x4
4!
+
x5
5!
+ . . .
38 / 44

39. Euler’s formula (2/2)
You can assume the expansion for ex holds when the exponent
x = iθ is purely imaginary. This means that
eiθ
= 1 + iθ +
(iθ)2
2!
+
(iθ)3
3!
+
(iθ)4
4!
+
(iθ)5
5!
+ . . .
= 1 + iθ −
θ2
2!
−
iθ3
3!
+
θ4
4!
+
iθ5
5!
+ . . .
= 1 −
θ2
2!
+
θ4
4!
. . .
!
+ i θ −
θ3
3!
+
iθ5
5!
+ . . .
!
= cos θ + i sin θ
Multiplication on both sides of this expression by a non-negative
real number r gives:
Theorem 1.16 (Euler’s formula)
r(cos θ + i sin θ) = reiθ
39 / 44

40. Example 1.17
I From Example 1.8, you know that
1 + i
√
3 = 2(cos(π/3) + i sin(π/3)). By Euler’s formula, it
follows that 1 + i
√
3 = 2eiπ/3.
I From Example 1.9, you know that
−1 + i
√
3 = 2(cos(2π/3) + i sin(2π/3)). So by Euler’s
formula, −1 + i
√
3 = 2ei2π/3.
I From Example 1.10, you know that
3 − 3i = 3
√
2(cos(−π/4) + i sin(−π/4)). Therefore
3 − 3i = 3
√
2e−iπ/4 by Euler’s formula.
40 / 44

41. Alternative ways of writing trig functions
You can use Euler’s formula to write trigonometric functions in
terms of exponentials. You know that
eiθ
= cos θ + i sin θ (1)
By the properties of sin and cos, you can write
e−iθ
= cos(−θ) + i sin(−θ) = cos θ − i sin θ (2)
Here, (1) - (2) is eiθ − e−iθ = 2i sin θ and so
sin θ =
eiθ − e−iθ
2i
You can also work out that cos θ =
eiθ + eiθ
2
.
41 / 44

42. Example 1.18
Using the fact that cos θ = (eiθ + e−iθ)/2, you can work out an
expression for cos3 θ. Here
cos3
(θ) =
eiθ + e−iθ
2
!3
=
1
23
eiθ
+ e−iθ
3
Using the binomial theorem and the laws of indices, you can write
cos3
θ =
1
23
(eiθ
)3
+ 3(eiθ
)2
e−iθ
+ 3eiθ
(e−iθ
)2
+ (e−iθ
)3
=
1
23
ei3θ
+ 3eiθ
+ 3e−iθ
+ e−3iθ
=
1
23
ei3θ
+ e−i3θ
+ 3(eiθ
+ e−iθ
)
Now 2 cos(3θ) = ei3θ + e−i3θ and 2 cos θ = eiθ + e−iθ. So
cos3
θ =
1
23
(2 cos(3θ) + 3(2 cos θ))
=
1
4
(cos(3θ) + 3 cos θ) 42 / 44

43. Sum formulas
Given two complex numbers z1 = eiθ1 and z2 = eiθ2 , you can use
the laws of exponents to get
z1z2 = eiθ1
eiθ2
= ei(θ1+θ2)
= cos(θ1 + θ2) + i sin(θ1 + θ2)
Writing z1 and z2 in polar form and multiplying gives
z1z2 = (cos θ1 + i sin θ1)(cos θ2 + i sin θ2)
= cos θ1 cos θ2 − sin θ1 sin θ2 + i(cos θ1 sin θ2 + cos θ2 sin θ1)
Equating real and imaginary parts for both expressions of z1z2 gives
cos(θ1 + θ2) = cos θ1 cos θ2 − sin θ1 sin θ2
sin(θ1 + θ2) = cos θ1 sin θ2 + cos θ2 sin θ1
You can use this to prove de Moivre’s theorem.
43 / 44

44. Euler’s identity
Setting θ = π in Euler’s formula gives
eiπ
= cos π + i sin π = −1 + 0i = −1
and so
Theorem 1.19 (Euler’s identity)
eiπ + 1 = 0
This result connects the five most fundamental mathematical
constants: 0, 1, π, e and i.
44 / 44