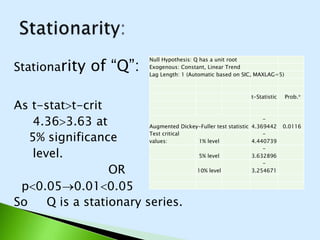
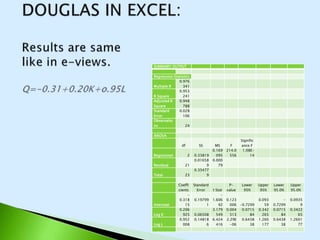
The document describes the Cobb-Douglas production function and the results of estimating its parameters. It finds that labor (L) and capital (K) explain 95% of the variation in output (Q) according to the estimated equation Q=-0.31+0.20K+0.95L. Diagnostic tests show the variables are stationary and there is no multicollinearity. The model is found to be statistically significant and a good fit to the data based on the F-statistic and R-squared value. It is determined that industry exhibits increasing returns to scale since the estimated coefficients of K and L sum to above 1.

1. Cobb-douglas production
function
Sub Topics
Background:
Definition:
Equation:
Diagnostic Tests:
Estimation of parameters in regression:

2. Background:
Developed by Paul
Douglas and C. W.
Cobb in the 1930’s.

3. Definition:
Cobb Douglas is a
Mathematical Formula that
relates Labor Capital and Output.
Cobb- Douglas equation:
Q=AKaLb

4. Cobb-douglas data file
Q K L
100 100 100
101 100 105
112 107 110
122 114 118
124 122 123
122 131 116
143 138 125
152 149 133
151 163 138
126 176 121
155 185 140
159 198 144
153 208 145
177 216 152
184 226 154
169 236 149
189 244 154
225 266 182
227 298 196
223 335 200
280 366 193
231 387 193
179 407 147
240 417 161

5. Log transformation for
regression Log Q Log K Log L
Following Formula is Used for
Log Transformation
=(log(A)) so on….
2 2 2
2.0043
21 2
2.0211
89
2.0492
18
2.0293
84
2.0413
93
2.0863
6
2.0569
05
2.0718
82
2.0934
22
2.0863
6
2.0899
05
2.0863
6
2.1172
71
2.0644
58
2.1553
36
2.1398
79
2.0969
1
2.1818
44
2.1731
86
2.1238
52
2.1789
77
2.2121
88
2.1398
79
2.1003
71
2.2455
13
2.0827
85
2.1903
32
2.2671
72
2.1461
28
2.2013
97
2.2966
65
2.1583
62
2.1846
91
2.3180
63
2.1613
68
2.2479
73
2.3344
54
2.1818
44
2.2648
18
2.3541
08
2.1875
21
2.2278
87
2.3729
12
2.1731
86
2.2764
62
2.3873
9
2.1875
21
2.3521
83
2.4248
82
2.2600
71

6. Diagnostic tests:
Results of normality test:
As p(Q,K,L)>0.05 so
series is Normally
Distributed.
Q K L
Mean 2.209588 2.299855 2.155283
Median 2.195864 2.307364 2.159865
Maximum 2.447158 2.620136 2.301030
Minimum 2.000000 2.000000 2.000000
Std. Dev. 0.124198 0.198841 0.087327
Skewness 0.058511 0.078104 0.107486
Kurtosis 2.104485 1.870039 2.151359
Jarque-Bera 0.815641 1.301213 0.766404
Probability 0.665098 0.521729 0.681675
Sum 53.03012 55.19651 51.72680
Sum Sq.
Dev. 0.354779 0.909371 0.175396
Observations 24 24 24

7. Stationarity:
Stationarity of “Q”:
As t-stat>t-crit
4.36>3.63 at
5% significance
level.
OR
Null Hypothesis: Q has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Automatic based on SIC, MAXLAG=5)
p<0.05®0.01<0.05
So Q is a stationary series.
t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -4.369442 0.0116
Test critical values: 1% level -4.440739
5% level -3.632896
10% level -3.254671

8. Null Hypothesis: K has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Automatic based on SIC, MAXLAG=4)
t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -4.007282 0.0250
Test critical values: 1% level -4.467895
5% level -3.644963
10% level -3.261452
Stationary of “k” :
As t-stat>t-crit
4.007>3.6 at
5% significance
level.
OR
p<0.05®0.025<0.05
So,
K is a stationary
series.

9. 9
Stationary of “L” :
As t-stat>t-crit
4.19>3.69 at
5% significance
level.
OR
p<0.05®0.02<0.05
So,
Q is a stationary series.
Null Hypothesis: L has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 4 (Automatic based on SIC, MAXLAG=4)
t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -4.196949 0.0200
Test critical
values: 1% level -4.571559
5% level -3.690814
10% level -3.286909

10. Multicolinearity:
Results of correlation test:
Results of Correlation
Test show that there
Exists high
Multicolinearity between
Q,K and L.
Q K L
Q 1.000000 0.919558 0.959428
K 0.919558 1.000000 0.878440
L 0.959428 0.878440 1.000000

11. Regression Analysis of C0bb-
Douglas P.F:
In E-views:

Here, α=0.206925 &
Adding α & β :
i.e α + β
0.206925+0.952008
=1.158>1
→ Industry exhibits
increasing returns
to scale
Variable Coefficient Std. Error t-Statistic Prob.
C -0.318155 0.197991 -1.606916 0.1230
LOGK 0.206925 0.065080 3.179549 0.0045
LOGL 0.952008 0.148186 6.424416 0.0000
R-squared 0.953241 Mean dependent var 2.209588
Adjusted R-squared 0.948788 S.D. dependent var 0.124198
S.E. of regression 0.028106 Akaike info criterion -4.189186
Sum squared resid 0.016589 Schwarz criterion -4.041929
Log likelihood 53.27023 Hannan-Quinn criter. -4.150119
F-statistic 214.0556 Durbin-Watson stat 2.247216
Prob(F-statistic) 0.000000

12. Interpretation of r-square:
 R-squared is a statistical measure. It is also known as the
coefficient of determination, or the coefficient of multiple
determination for multiple regression.
 It is the percentage of the response variable variation that is
explained by a linear model.
 → R-squared = Explained variation / Total variation
 R-squared is always between 0 and 100%:
 0% indicates that the model explains none of the variability
of the response data around its mean.
 100% indicates that the model explains all the variability of
the response data around its mean.

13. R-square=0.953241
95%variation in
Dependent variable are
Explained by independent
variable.
R-squared 0.953241 Mean dependent var 2.209588
Adjusted R-squared 0.948788 S.D. dependent var 0.124198
S.E. of regression 0.028106 Akaike info criterion -4.189186
Sum squared resid 0.016589 Schwarz criterion -4.041929
Log likelihood 53.27023 Hannan-Quinn criter. -4.150119
F-statistic 214.0556 Durbin-Watson stat 2.247216
Prob(F-statistic) 0.000000

14. Checking the signifacance of the
model:
Model is significant because :
Tkcal>Tcrit
3.179549>1.70
and
TLcal>Tcrit
6.424416>1.70

15. Checking the goodness of the
model:
fcal>fcrit
F>Fa(k-1,n-k)
214.0556>4.35
Hence the model is good

16. SUMMARY
OUTPUT
Regression
Statistics
Multiple R
0.9763
41
R Square
0.9532
41
Adjusted
R Square
0.9487
88
Standard
Error
0.0281
06
Observati
ons 24
ANOVA
df SS MS F
Significa
nce F
Regressio
n 2 0.33819
0.169
095
214.0
556
1.08E-
14
Residual 21 0.016589
0.000
79
Total 23 0.354779
Coeffic
ients
Standard
Error t Stat
P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept
-
0.3181
5 0.197991
-
1.606
92
0.123
006 -0.7299
0.0935
9 -0.7299 0.09359
Log K
0.2069
25 0.06508
3.179
549
0.004
513
0.07158
4
0.3422
65
0.07158
4
0.34226
5
Log L
0.9520
08 0.148186
6.424
416
2.29E
-06
0.64383
8
1.2601
77
0.64383
8
1.26017
7
REGRESSION ANALYSIS OF
COBB-DOUGLAS IN EXCEL:
Results are same
like in e-views.
Q=-0.31+0.20K+o.95L

17. The End…. ☺