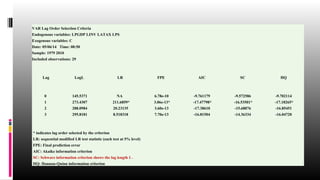
The document discusses the concept of cointegration and its various approaches, particularly focusing on the Engle-Granger and Johansen-Juselius methods. It outlines the conditions necessary for cointegration, interpretations of the Error Correction Model (ECM), and provides steps for conducting estimations using these methodologies. Additionally, it includes examples, definitions, and references for further reading on the subject.

3. Contents :
 Definition of Co-integration .
 Different Approaches of Co-integration.
 Johansen and Juselius (J.J) Co-integration.
 Error Correction Model (ECM).
 Interpretation of ECM term.
 Long – Run Co-integration Equation.

4. Definition of Co-integration
The concept of cointegration was first introduced by Granger
(1981) and elaborated further by Engle and Granger (1987), Engle
and Yoo (1987), Phillips and Ouliaris (1990), Stock and Watson
(1988), Phillips (1986 and 1987) and johansen (1988, 1991,
1995a).
Time series Yt and Xt are said to be cointegrated of order d,
where d > 0, written as Yt, Xt ~ CI (d). If
(a) Both series are integrated of order d,
(b) There exists a linear combination of these variables.

5. Examples :
 The old woman and the boy are
unrelated to one another, except
that they are both on a random
walk in the park. Information
about the boy's location tells us
nothing about the old woman's
location.
The old man and the dog are joined by one of
those leashes that has the cord rolled up inside
the handle on a spring. Individually, the dog and
the man are each on a random walk. They cannot
wander too far from one another because of the
leash. We say that the random processes
describing their paths are cointegrated.

6. Approaches of Co-integration :
Engle-Granger (1987)
Used when only one co
integrating vector is
under consideration
Johansen and Juselius
(1990)
Used when more than one co
integrating vector are under
consideration

7. Conditions Of Co-integration :
If all variables are stationary on level , we use
OLS method of estimation.
 If all variables or single variable are stationary on first
difference , we use Co-integration Method.
 If all the variables are stationary on first difference , we
use Johnson Co-integration and ARDL also.
 If some variables are stationary on level and some are
stationary on first difference , we only use ARDL model.

8. Johansen and Juselius (1990) J.J
Co-integration :
 If all the variables are stationary on first difference , we
use Johnson Co-integration.
 Although Johansen’s methodology is typically used in a
setting where all variables in the system are I(1), having
stationary variables in the system is theoretically not an
issue and Johansen (1995) states that there is little need to
pre-test the variables in the system to establish their order
of integration.

9. Johansen Co-integration :
 Johansen, Is a procedure for testing cointegration of
several I(1) time series. This test permits more than one
cointegrating relationship so is more generally applicable
than the engle–granger test .
 Yt = α0 + α1x1t + α2x2t + et
 Yt = α0 + α1x1t + α2x1t-1 + α3x2t + α4x2t-1 + et

10. Steps For Johnson Co-integration :
 STEP 1:-
 Check stationarity take only those variables which are
stationary at 1st difference.
 STEP 2:-
 File/new workfile/structured and dated/start date & end date
CLICK OK.
 Paste the data.
 STEP 3:-
 Quick/Group statistic/Co-integration test
 Write variables name CLICK OK

11. Date: 05/06/14 Time: 07:04
Sample (adjusted): 1981 2010
Included observations: 30 after adjustments
Trend assumption: Linear deterministic trend
Series: LPGDP LINV LATAX LPS
Lags interval (in first differences): 1 to 1
Steps of j-j cointegration
Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace 0.05
No. of CE(s) Eigenvalue Statistic Critical Value Prob.**
None * 0.620080 53.12601 47.85613 0.0147
At most 1 0.376331 24.09216 29.79707 0.1966
At most 2 0.265635 9.928096 15.49471 0.2863
At most 3 0.021943 0.665631 3.841466 0.4146
Trace test indicates 1 cointegrating eqn(s) at the 0.05 level

12. Definition of Error Correction Model
 If, then, Yr and Xt are cointegrated, by definition ftr ~ /
(0). Thus, we can express the relationship between Yt and
Xr with an ECM specification as:
ΔYt= a0 + b1ΔXt-μ^t-1 + Yt
 In this model, b1 is the impact multiplier (the short-run effect)
that measures the immediate impact that a change in Xt will
have on a change in Yt . On the other hand πt is the feedback
effect, or the adjustment effect, and shows how much of this
disequilibrium is being corrected.

13. Steps For VAR Estimate :
STEPS :-
Quick /Estimate VAR
VAR type: Vector Error Correction.
Endogenous variables:- All variables name
Lag intervals:-1 ,1
 CLICK OK

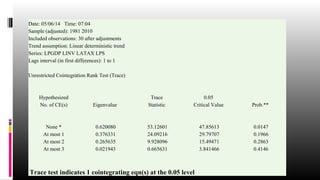
14. Vector Error Correction Estimates
Date: 05/26/14 Time: 22:36
Sample (adjusted): 1981 2010
Included observations: 30 after adjustments
Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq: CointEq1
LPGDP(-1) 1.000000
LINV(-1) -4.620559
(0.47459)
[-9.73587]
LATAX(-1) -3.350165
(1.20384)
[-2.78289]
LPS(-1) 1.274220
(0.49822)
[ 2.55755]
C -3.861790
Error Correction: D(LPGDP) D(LINV) D(LATAX) D(LPS)
CointEq1 -0.011599 0.167417 -0.004750 -0.060848
(0.02160) (0.04974) (0.02840) (0.03017)
[-0.53695] [ 3.36570] [-0.16725] [-2.01682]

15. Estimation of ECM value :
 If T value is 1.67 or more than 1.70 then we conclude that
variable is significant….
 OR when Tcal is > 1.70 or when Tcal = 1.67
 We conclude variable is significant…
 Where there’s –ve sign we consider it +ve as the value of
Linv is -4.62 we consider it +ve and conclude that the there is
+ve relationship between lpgdp and linv……
 In Coint Equ 1 the value of Lpgdp is -0.01 which shows
Convergence to equilibrium and 1 % convergance in one year

16. Lag Length Criteria :
STEPS :-
 Go to The view of result window of VAR Estimate.
 Go to Lag Length Structure and select Lag Length
Criteria.
 In Lag specification Select the lags to include as 3.
 Click OK

17. VAR Lag Order Selection Criteria
Endogenous variables: LPGDP LINV LATAX LPS
Exogenous variables: C
Date: 05/06/14 Time: 08:50
Sample: 1979 2010
Included observations: 29
Lag LogL LR FPE AIC SC HQ
0 145.5371 NA 6.78e-10 -9.761179 -9.572586 -9.702114
1 273.4307 211.6859* 3.06e-13* -17.47798* -16.53501* -17.18265*
2 288.0984 20.23135 3.60e-13 -17.38610 -15.68876 -16.85451
3 295.8181 8.518318 7.70e-13 -16.81504 -14.36334 -16.04720
* indicates lag order selected by the criterion
LR: sequential modified LR test statistic (each test at 5% level)
FPE: Final prediction error
AIC: Akaike information criterion
SC: Schwarz information criterion shows the lag length 1 .
HQ: Hannan-Quinn information criterion

18. Long Run Equation For Results :
 LPGDP = α + β1 LINV + β2 LATAX + β3 LPS
LPGDP = 3.86 +4.62 LINV + 3.35
LATAX – 1.27 LPS.

19. REFRENCES :
 http://www.google.com.pk/url?
sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0CCkQFjAA&url=http%3A%2F
%2Fwww.eco.uc3m.es%2Fjgonzalo%2Fteaching%2FtimeseriesMA
%2Fspuriousregandcointegration.ppt&ei=3IWDU8KIFKXm7Aa1q4GgAQ&usg=AFQjCNEM
eDrxYrVbmOezMTPaUHqr7Fmsbw&sig2=oDcwQxDEQ64CZxFKeobvkg&bvm=bv.677202
77,d.ZGU
 powershow.com/view/9d319-
MzYzM/TIME_SERIES_REGRESSION_COINTEGRATION_powerpoint_ppt_presentation
 .google.com.pk/url?
sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0CDMQFjAB&url=http%3A%2F
%2Fwww.uh.edu%2F~bsorense
%2Fcoint.pdf&ei=SIiDU5vzFuSU7QbNpYC4Dw&usg=AFQjCNFCyaKrvkcaE_VVe8Gwmh
EeMv46Iw&sig2=sRUVQeVm32aykeFpV2Ds7w
 https://www.imf.org/external/pubs/ft/wp/2007/wp07141.pdf
 Applied Economics By Esterio.
 Basic Econometrics By Damodar Gujrati.