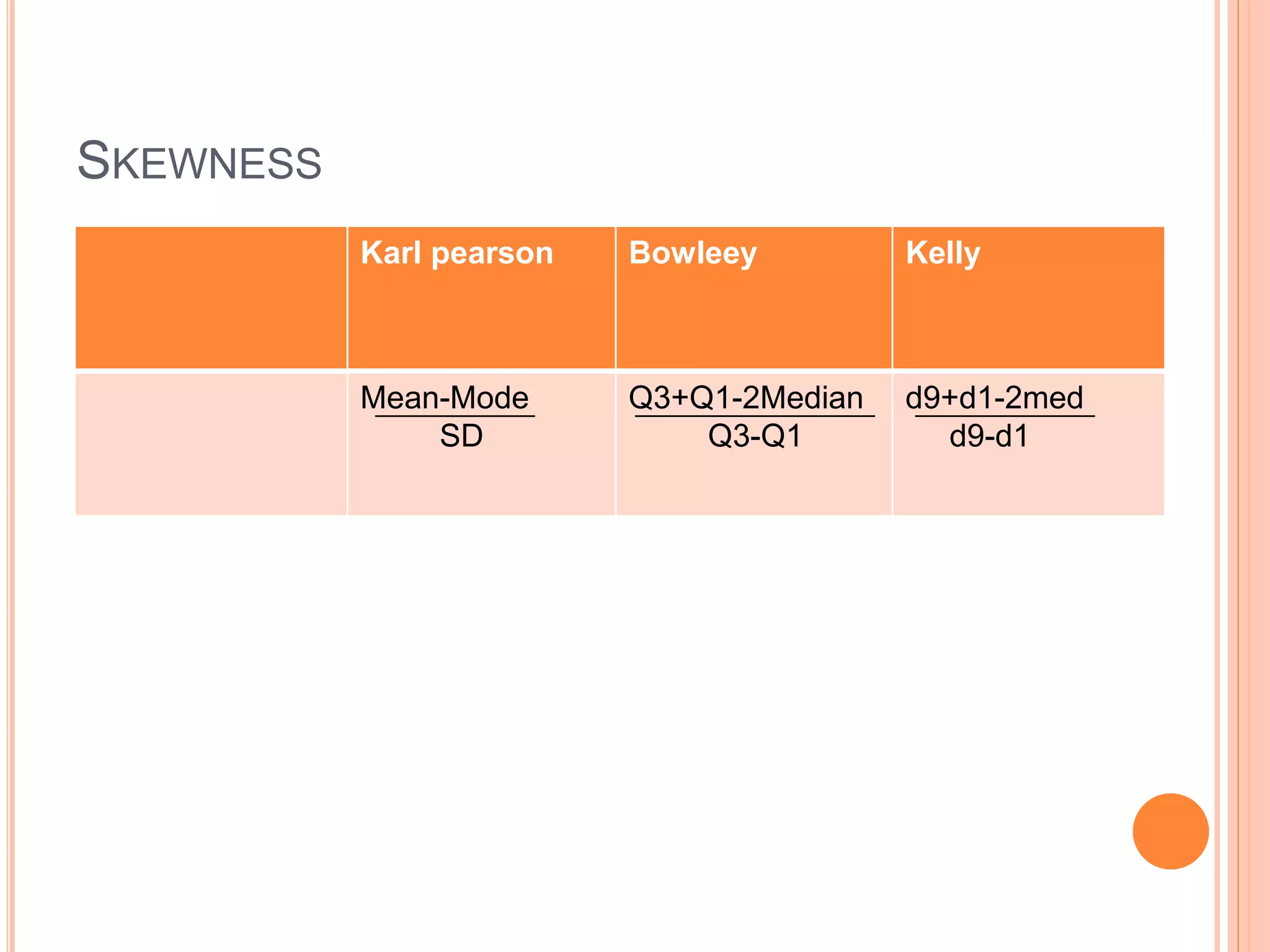
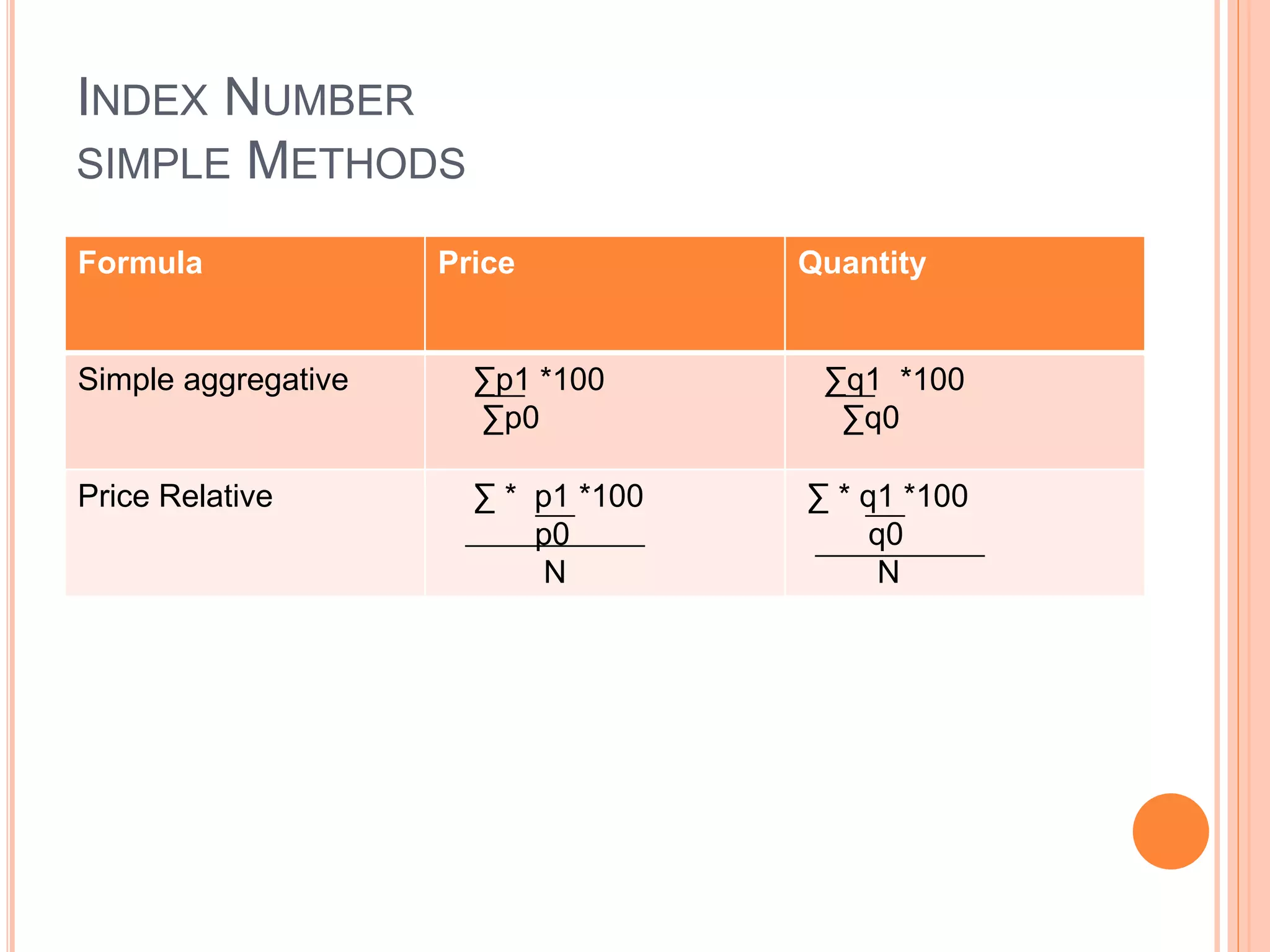
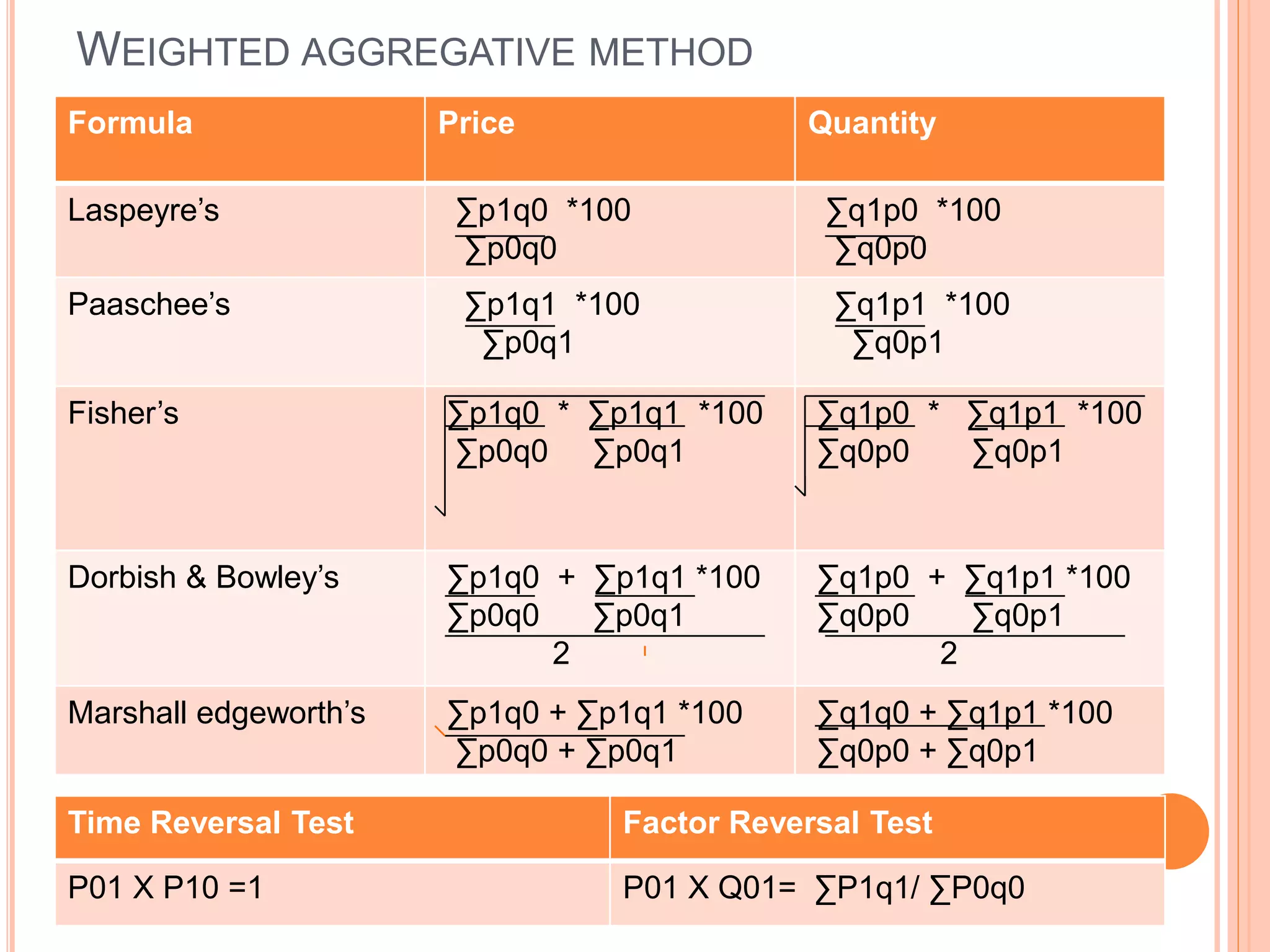
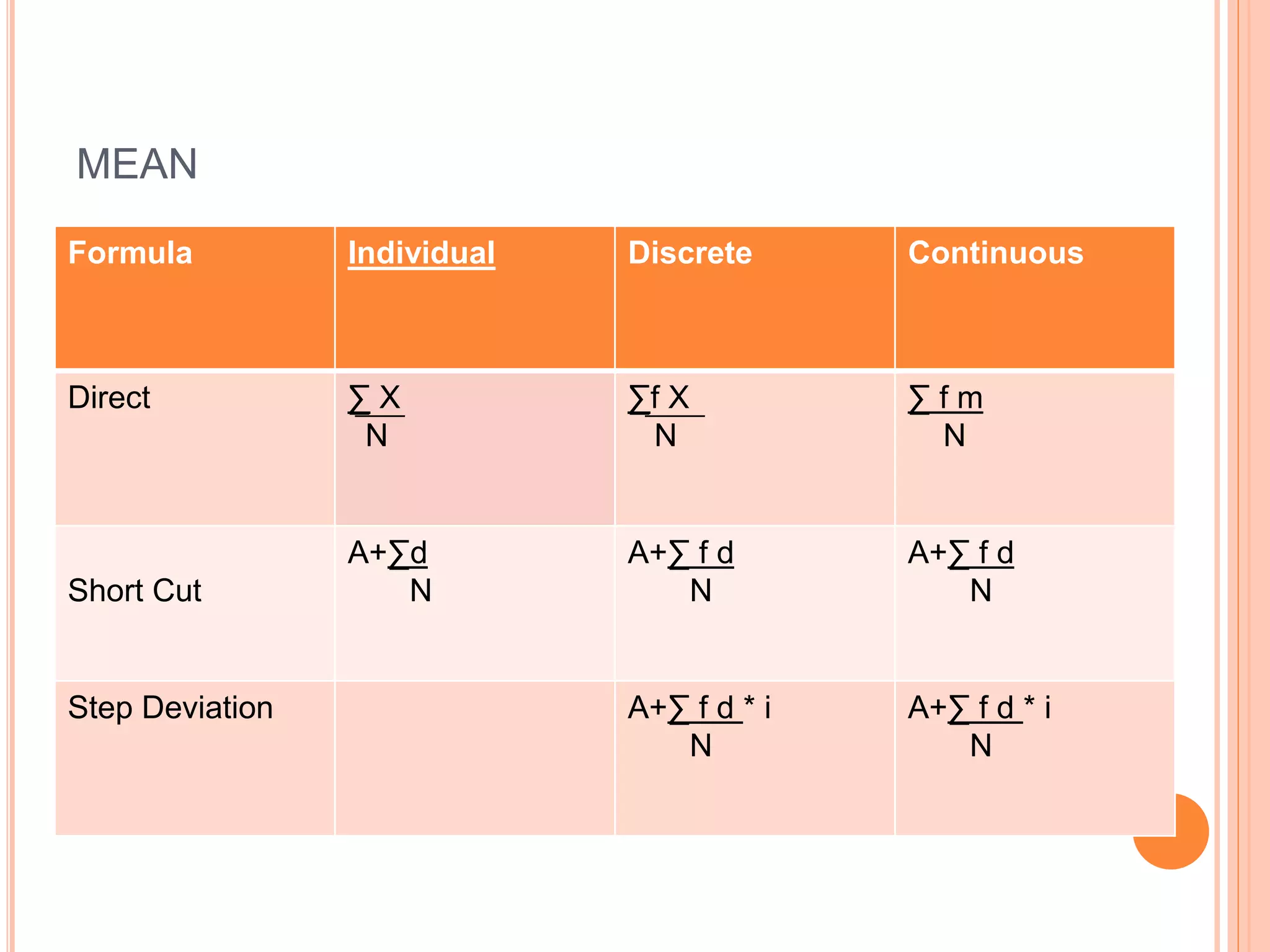
This document contains formulas for various statistical measures including mean, median, mode, range, quartiles, mean deviation, standard deviation, correlation, and regression. It provides formulas for calculating these measures using direct, short cut, and step deviation methods for both discrete and continuous data. Formulas are also included for weighted mean, index numbers, skewness, and time series analysis.

1. BADDI UNIVERSITY OF EMERGING
SCIENCE AND TECHNOLOGY
STATISTICS FORMULA’S
Sahil Gautam
17PBA058

2. MEAN
Formula Individual Discrete Continuous
Direct ∑ X
N
∑f X
N
∑ f m
N
Short Cut
A+∑d
N
A+∑ f d
N
A+∑ f d
N
Step Deviation A+∑ f d * i
N
A+∑ f d * i
N

3. COMBINED MEAN WEIGHTED MEAN
N1 X1 + N2 X2
N1 + N2
∑ W X
∑ W

4. MEDIAN
Individual Continuous
N+1/2(when in points add L+U/2) N -cf
M= 2 *i
f

5. MODE
Z= L1+ f1-f0 *i or Z= 3Meadian-2Mean
2f1-f0-f2

6. RANGE
Range (R) = Largest value- Small value (L-S)
Cofficient CR= L-S
L+S

7. QUARTILES DEVIATION
Individual Contionuos
Q1= N+1
4
Q3 = [3(N+1)]
4
QD= Q3-Q1
2
N – cf
QD= L+ 4 *i
f
Coeff. = Q3-Q1
Q3+Q1

8. MEAN DEVIATION
Individual Discrete &
Continuous
Cofficent
MD= ∑ d
N
MD= ∑f d
N
MD
Median or Mean

9. STANDARD DEVIATION
C Direct Short cut Step deviation
Individual SD= ∑ (X-X)
N
2
∑dx2 - ∑dx
N N
∑dx2 - ∑dx 2 *C
N N
Discrete &
Continuous
∑fdx2 - ∑fdx 2
N N
∑dx2 - ∑dx 2 *C
N N

10. COEFFICIENT OF SD AND COEFFICIENT OF
VARIATION OR C.VD
Coefficient of SD Coefficient of Variation or
C.VD
=σ
x
= σ *100
x
Combined SD = N1σ 1 + N2σ 2 + N1d1 + N2d2
N1 + N2

11. SKEWNESS
Karl pearson Bowleey Kelly
Mean-Mode
SD
Q3+Q1-2Median
Q3-Q1
d9+d1-2med
d9-d1

12. INDEX NUMBER
SIMPLE METHODS
Formula Price Quantity
Simple aggregative ∑p1 *100
∑p0
∑q1 *100
∑q0
Price Relative ∑ * p1 *100
p0
N
∑ * q1 *100
q0
N

13. WEIGHTED AGGREGATIVE METHOD
Formula Price Quantity
Laspeyre’s ∑p1q0 *100
∑p0q0
∑q1p0 *100
∑q0p0
Paaschee’s ∑p1q1 *100
∑p0q1
∑q1p1 *100
∑q0p1
Fisher’s ∑p1q0 * ∑p1q1 *100
∑p0q0 ∑p0q1
∑q1p0 * ∑q1p1 *100
∑q0p0 ∑q0p1
Dorbish & Bowley’s ∑p1q0 + ∑p1q1 *100
∑p0q0 ∑p0q1
2
∑q1p0 + ∑q1p1 *100
∑q0p0 ∑q0p1
2
Marshall edgeworth’s ∑p1q0 + ∑p1q1 *100
∑p0q0 + ∑p0q1
∑q1q0 + ∑q1p1 *100
∑q0p0 + ∑q0p1
Time Reversal Test Factor Reversal Test
P01 X P10 =1 P01 X Q01= ∑P1q1/ ∑P0q0

14. CORRELATION
A-KARL PEARSON
Actual mean r = ∑xy
∑x2 . ∑y2
Assumed mean r = N. ∑dxdy-∑dx. ∑dy
N.∑dx2 –(∑dx)2 . N. ∑dy 2 – (∑dy)2
Actual data r = N. ∑XY-∑X. ∑Y
N. ∑X 2 – (∑X)2 . N.∑Y2 – (∑Y)2

15. REGRESSION
A-LEAST SQUARE METHOD
(using normal equation)
1. Y on X
Y= a+bX
∑Y = Na + b∑X
∑XY = a∑X + b∑X 2
2. X on Y
X= a+ bY
∑X= Na+ b∑Y
∑XY= a∑Y + b∑Y2
B- Equation using coefficient (Using Mean)
1. Y on X
Y-Y= byx (X-X)
byx= N. ∑xy-∑x. ∑y
N. ∑x2 – (∑x)2
2. X on Y
X-X= bxy (Y-Y)
bxy= N. ∑xy-∑y. ∑x
N. ∑y2- (∑y)2

16. (Assumed Mean)
1. Y on X
Y-Y = byx(X-X)
byx= N. ∑dxdy-∑dx. ∑dy
N. ∑dx2 – (∑dx)2
2. X on Y
X-X=bxy(Y-Y)
bxy= N. ∑dxdy- ∑dy. ∑dx
N. ∑dy2- (∑dy)2
Time Series
Least Square Method
yc= a+bx
If x=0 then
a= ∑y
N
b= ∑xy
∑x2