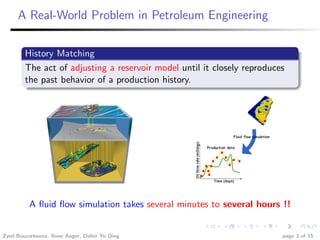
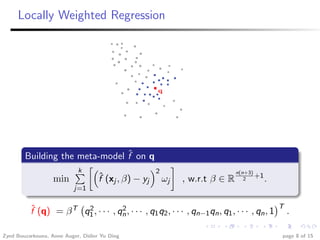
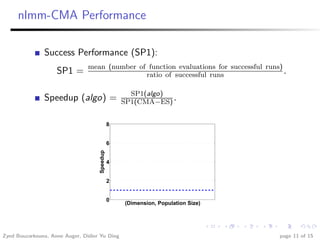
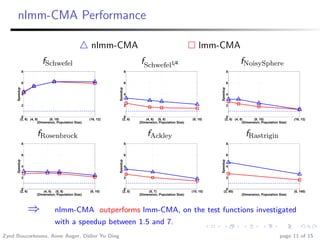
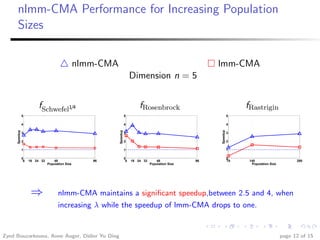
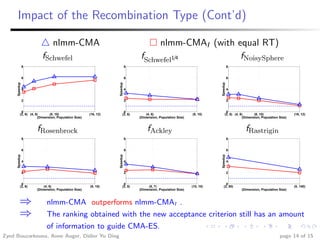
This document summarizes research investigating the use of local meta-models within the CMA-ES optimization algorithm for large population sizes. It introduces CMA-ES, describes how local meta-models can be used to build surrogate models of the objective function to reduce evaluations, and presents a new variant called nlmm-CMA that uses a more flexible acceptance criterion for the meta-model. Experimental results show nlmm-CMA achieves speedups over lmm-CMA, the prior local meta-model approach for CMA-ES, on benchmark optimization problems.

1. Investigating the Local-Meta-Model CMA-ES for
Large Population Sizes
Zyed Bouzarkouna1,2 Anne Auger2 Didier Yu Ding1
1 IFP (Institut Fran¸ais du P´trole)
c e
2 TAO Team, INRIA Saclay-Ile-de-France, LRI
April 07, 2010

2. Statement of the Problem
Objective
To solve a real-world optimization problem formulated in a
black-box scenario with an objective function f : Rn → R.
multimodal non-smooth
noisy non-convex
f may be:
non-separable computationally expensive
...
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 2 of 15

3. A Real-World Problem in Petroleum Engineering
History Matching
The act of adjusting a reservoir model until it closely reproduces
the past behavior of a production history.
A fluid flow simulation takes several minutes to several hours !!
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 3 of 15

4. Statement of the Problem (Cont’d)
Difficulties
Evolutionary Algorithms (EAs) are usually able to cope with
noise, multiple optima . . .
Computational cost
build a model of f , based on true evaluations ;
use this model during the optimization to save evaluations.
⇒ How to decide whether:
the quality of the model is good enough to continue
exploiting this model ?
or
new evaluations on the “true” objective function should be
performed ?
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 4 of 15

5. Table of Contents
1 CMA-ES with Local-Meta-Models
Covariance Matrix Adaptation-ES
Locally Weighted Regression
Approximate Ranking Procedure
2 A New Variant of lmm-CMA
A New Meta-Model Acceptance Criterion
nlmm-CMA Performance
3 Conclusions
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 5 of 15

6. Covariance Matrix Adaptation-ES
CMA-ES (Hansen & Ostermeier 2001)
Initialize distribution parameters m, σ and C, set population size
λ ∈ N.
while not terminate
Sample xi = m + σNi (0, C), for i = 1 . . . λ according to a
multivariate normal distribution
Evaluate x1 , . . . , xλ on f
Update distribution parameters
(m, σ, C) ← (m, σ, C, x1 , . . . , xλ , f (x1 ), . . . , f (xλ ))
where
m ∈ Rn : the mean of the multivariate normal distribution
σ ∈ R+ : the step-size
C ∈ Rn×n : the covariance matrix.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 6 of 15

7. Covariance Matrix Adaptation-ES (Cont’d)
Moving the mean
µ(= λ )
2
m= ωi xi:λ .
i=1
where xi:λ is the i th ranked individual:
f (x1:λ ) ≤ . . . f (xµ:λ ) ≤ . . . f (xλ:λ ) ,
Pµ
ω1 ≥ . . . ≥ ωµ > 0, ωi = 1.
i=1
Other updates
Adapting the Covariance Matrix
Step-Size Control
⇒ Updates rely on the ranking of individuals according to f and
not on their exact values on f .
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 7 of 15

8. Locally Weighted Regression
q ∈ Rn : A point to evaluate
⇒ ˆ
f (q) : a full quadratic meta-model on q.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 8 of 15

9. Locally Weighted Regression
A training set containing m points with their objective function
values (xj , yj = f (xj )) , j = 1..m
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 8 of 15

10. Locally Weighted Regression
We select the k nearest neighbor data points to q according to
Mahalanobis distance with respect to the current covariance matrix
C.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 8 of 15

11. Locally Weighted Regression
h is the bandwidth defined by the distance of the k th nearest
neighbor data point to q.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 8 of 15

12. Locally Weighted Regression
ˆ
Building the meta-model f on q
k 2 n(n+3)
min ˆ
f (xj , β) − yj ωj , w.r.t β ∈ R 2
+1
.
j=1
ˆ T
f (q) = β T q1 , · · · , qn , · · · , q1 q2 , · · · , qn−1 qn , q1 , · · · , qn , 1
2 2 .
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 8 of 15

13. Approximate Ranking Procedure
Every generation g , CMA-ES has λ points to evaluate.
⇒ Which are the points that must be evaluated with:
the true objective function f ?
ˆ
the meta-model f ?
Approximate ranking procedure (Kern et al. 2006)
1 ˆ
approximate f and rank the µ best individuals
2 evaluate f on the ninit best individuals
“ λ−n ”
3 for nic := 1 to n
init do
b
4 ˆ
approximate f and rank the µ best individuals
5 if (the exact ranking of the µ best individuals changes) then
6 evaluate f on the nb best unevaluated individuals
7 else
8 break
9 fi
10 od
11 adapt ninit depending on nic
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 9 of 15

14. A New Meta-Model Acceptance Criterion
Requiring the preservation of the exact ranking of the µ best
individuals is a too conservative criterion to measure the quality of
the meta-model.
New acceptance criteria (nlmm-CMA)
The meta-model is accepted if it succeeds in keeping:
the best individual and the ensemble of the µ best individuals
unchanged
or
the best individual unchanged, if more than one fourth of the
population is evaluated.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 10 of 15

15. nlmm-CMA Performance
Success Performance (SP1):
mean (number of function evaluations for successful runs)
SP1 = ratio of successful runs .
SP1(algo)
Speedup (algo) = SP1(CMA−ES) .
8
6
Speedup
4
2
0
(Dimension, Population Size)
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 11 of 15

16. nlmm-CMA Performance
nlmm-CMA lmm-CMA
fSchwefel fSchwefel1/4 fNoisySphere
8 8 8
6 6 6
Speedup
Speedup
Speedup
4 4 4
2 2 2
0 0 0
(2, 6) (4, 8) (8, 10) (16, 12) (2, 6) (4, 8) (5, 8) (8, 10) (2, 6) (4, 8) (8, 10) (16, 12)
(Dimension, Population Size) (Dimension, Population Size) (Dimension, Population Size)
fRosenbrock fAckley fRastrigin
8 8 8
6 6 6
Speedup
Speedup
Speedup
4 4 4
2 2 2
0 0 0
(2, 6) (4, 8) (5, 8) (8, 10) (2, 5) (5, 7) (10, 10) (2, 50) (5, 140)
(Dimension, Population Size) (Dimension, Population Size) (Dimension, Population Size)
⇒ nlmm-CMA outperforms lmm-CMA, on the test functions investigated
with a speedup between 1.5 and 7.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 11 of 15

17. nlmm-CMA Performance for Increasing Population
Sizes
nlmm-CMA lmm-CMA
Dimension n = 5
fSchwefel1/4 fRosenbrock fRastrigin
5 5 5
4 4 4
Speedup
Speedup
Speedup
3 3 3
2 2 2
1 1 1
0 0 0
8 16 24 32 48 96 8 16 24 32 48 96 70 140 280
Population Size Population Size Population Size
⇒ nlmm-CMA maintains a significant speedup,between 2.5 and 4, when
increasing λ while the speedup of lmm-CMA drops to one.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 12 of 15

18. Impact of the Recombination Type
nlmm-CMA
a default weighted recombination type
ln(µ+1)−ln(i)
ωi = µ ln(µ+1)−ln(µ!) , for i = 1 . . . µ.
nlmm-CMAI
an intermediate recombination type
1
ωi = µ , for i = 1 . . . µ.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 13 of 15

19. Impact of the Recombination Type (Cont’d)
nlmm-CMA nlmm-CMAI (with equal RT)
fSchwefel fSchwefel1/4 fNoisySphere
8 8 8
6 6 6
Speedup
Speedup
Speedup
4 4 4
2 2 2
0 0 0
(2, 6) (4, 8) (8, 10) (16, 12) (2, 6) (4, 8) (8, 10) (2, 6) (4, 8) (8, 10) (16, 12)
(Dimension, Population Size) (Dimension, Population Size) (Dimension, Population Size)
fRosenbrock fAckley fRastrigin
8 8 8
6 6 6
Speedup
Speedup
Speedup
4 4 4
2 2 2
0 0 0
(2, 6) (4, 8) (8, 10) (2, 5) (5, 7) (10, 10) (2, 50) (5, 140)
(Dimension, Population Size) (Dimension, Population Size) (Dimension, Population Size)
⇒ nlmm-CMA outperforms nlmm-CMAI .
⇒ The ranking obtained with the new acceptance criterion still has an amount
of information to guide CMA-ES.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 14 of 15

20. Summary
CMA-ES with meta-models
The speedup of lmm-CMA with respect to CMA-ES drops to one when the population
size λ increases.
⇒ The meta-model acceptance criterion is too conservative.
New variant of CMA-ES with meta-models
A new meta-model acceptance criterion: It must keep:
the best individual and the ensemble of the µ best individuals unchanged
the best individual unchanged, if more than one fourth of the population
is evaluated.
nlmm-CMA outperforms lmm-CMA on the test functions investigated with a
speedup in between 1.5 and 7.
nlmm-CMA maintains a significant speedup, between 2.5 and 4, when
increasing the population size on tested functions.
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 15 of 15

21. Thank You For Your Attention
Zyed Bouzarkouna, Anne Auger, Didier Yu Ding page 16 of 15

22. Investigating the Local-Meta-Model CMA-ES for
Large Population Sizes
Zyed Bouzarkouna1,2 Anne Auger2 Didier Yu Ding1
1 IFP (Institut Fran¸ais du P´trole)
c e
2 TAO Team, INRIA Saclay-Ile-de-France, LRI
April 07, 2010