Download as PDF, PPTX
Uploaded bySaroosh Shabbir
Classical and Quantum Interference
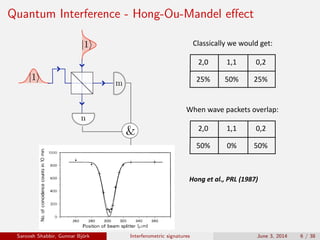
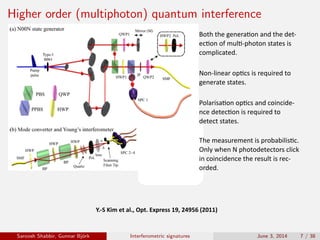
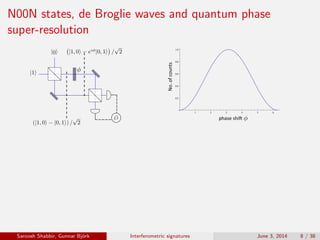
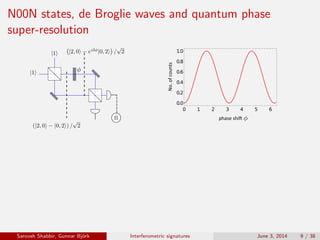
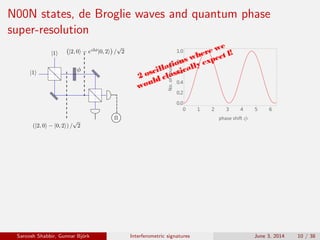
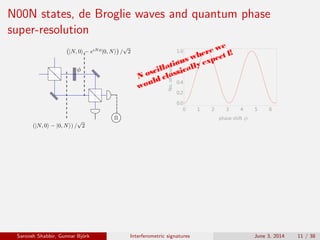
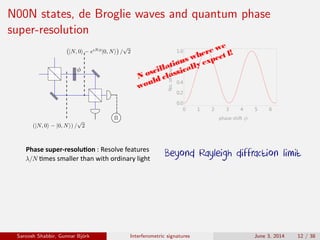
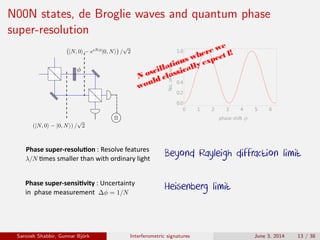
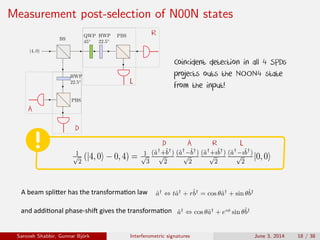
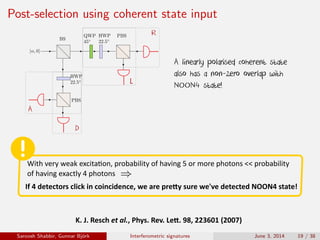
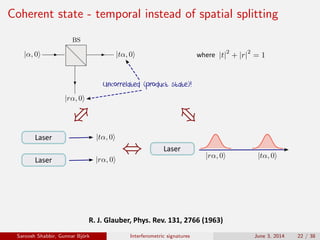
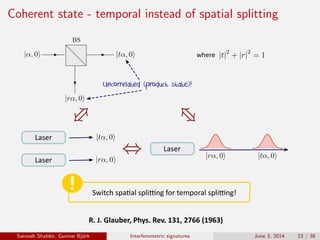
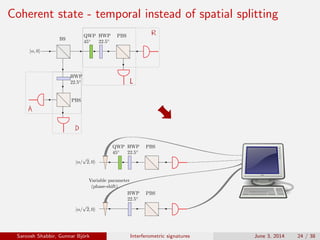
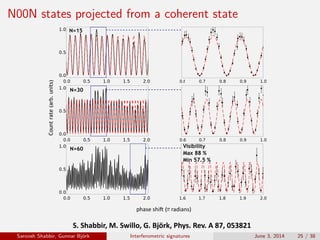
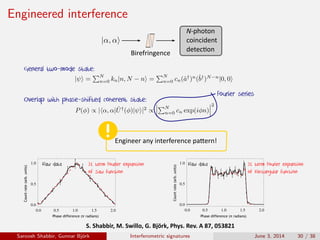
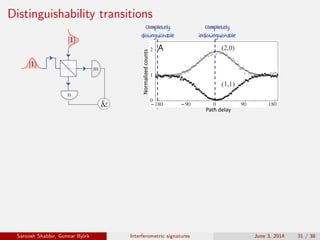
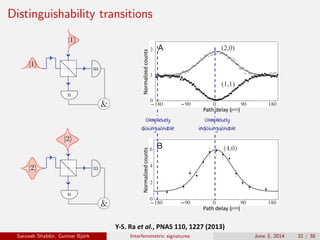
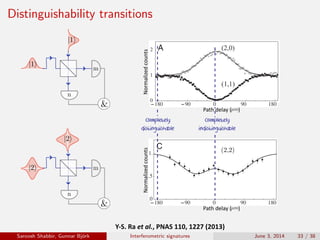
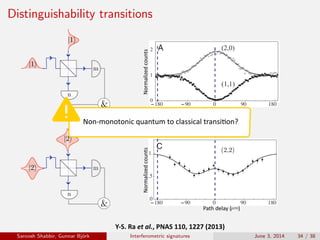
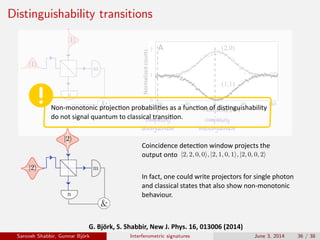
The document discusses the interferometric signatures of quantum and classical light states, exploring their fundamental differences and transformation characteristics. It also covers various interference phenomena including first and second order interference and highlights quantum interference effects such as the Hong-Ou-Mandel effect and the generation and detection of multi-photon states. The findings emphasize the significance of advanced measurement techniques for distinguishing quantum behaviors from classical optics.
More Related Content
Similar to Classical and Quantum Interference
Classical and Quantum Interference
- 1.
- 2. Interferometric signatures ofquantum and classical states Do interferometric signals of quantum states differ fundam- entally from classical states, in terms of shape and visibility? How do the interferometric signals vary as states are trans- formed from quantum to classical? Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 1 / 38
- 3. Outline Interference - From Huygens & Young to Hanbury Brown & Twiss Higher order interference Two-mode projec�on measurements Quantum interference from semi-classical states Engineered interference Projec�on measurements of increasingly dis�nguishable states Summary and Conclusions Saroosh Shabbir, GunnarBj¨ork Interferometric signatures June 3, 2014 2 / 38
- 4. Classical Interference -First order Unfiltered 605 nm, FWHM 5 nm HeNe laser Chris�an Huygens (1629-1659) Thomas Young (1773-1829) All single mode states display first order interference. First order interference does not discriminate between states. It thus does not separate classical from quantum. Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 3 / 38
- 5. Second order interference Robert Hanbury Brown (1916-2002) Richard Twiss (1920-2005) Intensi�es can also be correlated and have a coherence length associated to the emi�ng light source. R. Hanbury Brown & R. Twiss, Nature 178, 1046-1048 (1956) SarooshShabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 4 / 38
- 6. Quantum Interference -Hong-Ou-Mandel effect 2,0 1,1 0,2 25% 50% 25% Classically we would get: 2,0 1,1 0,2 50% 0% 50% When wave packets overlap: Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 5 / 38
- 7. Quantum Interference -Hong-Ou-Mandel effect 2,0 1,1 0,2 25% 50% 25% Classically we would get: 2,0 1,1 0,2 50% 0% 50% When wave packets overlap: Hong et al., PRL (1987) Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 6 / 38
- 8. Higher order (multiphoton)quantum interference Y.-S Kim et al., Opt. Express 19, 24956 (2011) Both the genera�on and the det- ec�on of mul�-photon states is complicated. Non-linear op�cs is required to generate states. Polarisa�on op�cs and coincide- nce detec�on is required to detect states. The measurement is probabilis�c. Only when N photodetectors click in coincidence the result is rec- orded. Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 7 / 38
- 9. N00N states, deBroglie waves and quantum phase super-resolution 1 2 3 4 5 6 0.2 0.4 0.6 0.8 1.0 phase shi� No. of counts Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 8 / 38
- 10. N00N states, deBroglie waves and quantum phase super-resolution phase shi� No. of counts 0 1 2 3 4 5 6 0.0 0.2 0.4 0.6 0.8 1.0 Phase difference Countrate Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 9 / 38
- 11. N00N states, deBroglie waves and quantum phase super-resolution 2 oscillations where we would classically expect 1! Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 10 / 38
- 12. N00N states, deBroglie waves and quantum phase super-resolution N oscillations where we would classically expect 1! Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 11 / 38
- 13. N00N states, deBroglie waves and quantum phase super-resolution N oscillations where we would classically expect 1! Phase super-resolu�on : Resolve features �mes smaller than with ordinary light Beyond Rayleigh diffraction limit Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 12 / 38
- 14. N00N states, deBroglie waves and quantum phase super-resolution N oscillations where we would classically expect 1! Phase super-sensi�vity : Uncertainty in phase measurement Phase super-resolu�on : Resolve features �mes smaller than with ordinary light Beyond Rayleigh diffraction limit Heisenberg limit J. Jacobson, G. Björk, I. Chuang, and Y. Yamamoto, PRL 74, 4835-4838 (1995)Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 13 / 38
- 15. Measurement post-selection ofN00N states given that we have only available. Suppose we want to project out the state Write the wanted state as Form the polynomial and factorise over complex numbers Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 14 / 38
- 16. Measurement post-selection ofN00N states given that we have only available. Suppose we want to project out the state Write the wanted state as Form the polynomial and factorise over complex numbers Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 15 / 38
- 17. Measurement post-selection ofN00N states given that we have only available. Suppose we want to project out the state Write the wanted state as Form the polynomial and factorise over complex numbers D A R L Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 16 / 38
- 18. Measurement post-selection ofN00N states given that we have only available. Suppose we want to project out the state Write the wanted state as Form the polynomial and factorise over complex numbers D A R L A beam spli�er has the transforma�on law and addi�onal phase-shi� gives the transforma�on Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 17 / 38
- 19. Measurement post-selection ofN00N states D A R L A beam spli�er has the transforma�on law and addi�onal phase-shi� gives the transforma�on Coincident detection in all 4 SPDs projects outs the NOON4 state from the input! R L A D Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 18 / 38
- 20. Post-selection using coherentstate input A linearly polarised coherent state also has a non-zero overlap with NOON4 state! R L A D With very weak excita�on, probability of having 5 or more photons << probability of having exactly 4 photons If 4 detectors click in coincidence, we are pre�y sure we've detected NOON4 state! K. J. Resch et al., Phys. Rev. Le�. 98, 223601 (2007) Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 19 / 38
- 21. Quantum optics fromsemi-classical states A linearly polarised coherent state also has a non-zero overlap with NOON4 state! R L A D With very weak excita�on, probability of having 5 or more photons << probability of having exactly 4 photons If 4 detectors click in coincidence, we are pre�y sure we've detected NOON4 state! K. J. Resch et al., Phys. Rev. Le�. 98, 223601 (2007) Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 20 / 38
- 22. Generalising the projectionmeasurement method Any complex polynomial can be factored over the field of complex numbers. Mathematical Theorem: Implication: The corresponding projector to any N-photon, two-mode state can be implemented through a series of beam-spli�ers, polarising op�cs, and signle photon coincidence measurements! Example: Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 21 / 38
- 23. Coherent state -temporal instead of spatial splitting Uncorrelated (product state)! R. J. Glauber, Phys. Rev. 131, 2766 (1963) where Laser Laser Laser Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 22 / 38
- 24. Coherent state -temporal instead of spatial splitting Uncorrelated (product state)! R. J. Glauber, Phys. Rev. 131, 2766 (1963) where Laser Laser Laser Switch spa�al spli�ng for temporal spli�ng! Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 23 / 38
- 25. Coherent state -temporal instead of spatial splitting R L A D Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 24 / 38
- 26. N00N states projectedfrom a coherent state 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 N=30 N=60 Countrate(arb.units) 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 N=15 Phase difference (π radians) ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 0.6 0.7 0.8 0.9 1.0 1.6 ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 1.7 1.8 1.9 2.0 ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 0.6 0.7 0.8 0.9 1.0 Visibility Max 88 % Min 57.5 % 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 N=30 N=60 Countrate(arb.units) 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 N=15 Phase difference (π radians) ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 0.6 0.7 0.8 0.9 1.0 1.6 ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 1.7 1.8 1.9 2.0 ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 0.6 0.7 0.8 0.9 1.0 Visibility Max 88 % Min 57.5 % phase shi� radians) ( S. Shabbir, M. Swillo, G. Björk, Phys. Rev. A 87, 053821 Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 25 / 38
- 27. Arbitrary interference ausing coherent state S. Shabbir, M. Swillo, G. Björk, Phys. Rev. A 87, 053821 Birefringence N-photon coincident detec�on General two-mode state: Overlap with phase-shifted coherent state: Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 26 / 38
- 28. Arbitrary interference ausing coherent state S. Shabbir, M. Swillo, G. Björk, Phys. Rev. A 87, 053821 Fourier series Birefringence N-photon coincident detec�on General two-mode state: Overlap with phase-shifted coherent state: Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 27 / 38
- 29. Arbitrary interference ausing coherent state S. Shabbir, M. Swillo, G. Björk, Phys. Rev. A 87, 053821 Fourier series Birefringence N-photon coincident detec�on General two-mode state: Overlap with phase-shifted coherent state: Engineer any interference pa�ern! Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 28 / 38
- 30. Engineered interference S. Shabbir, M. Swillo, G. Björk, Phys. Rev. A 87, 053821 Fourier series Birefringence N-photon coincident detec�on Generaltwo-mode state: Overlap with phase-shifted coherent state: Engineer any interference pa�ern! ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 Phase difference (π radians) Countrate(arb.units) 31 term Fourier expansion of Saw function Raw data Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 29 / 38
- 31. Engineered interference S. Shabbir, M. Swillo, G. Björk, Phys. Rev. A 87, 053821 Fourier series Birefringence N-photon coincident detec�on Generaltwo-mode state: Overlap with phase-shifted coherent state: Engineer any interference pa�ern! ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 Phase difference (π radians) Countrate(arb.units) ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 Phase difference (π radians) Countrate(arb.units) 31 term Fourier expansion of Saw function Raw data 31 term Fourier expansion of Rectangular function Raw data Saroosh Shabbir, Gunnar Bj¨ork Interferometric signatures June 3, 2014 30 / 38
- 32. Distinguishability transitions Normalized counts Path delay Completely indistinguishable Completely distinguishable Saroosh Shabbir,Gunnar Bj¨ork Interferometric signatures June 3, 2014 31 / 38
- 33. Distinguishability transitions Normalized counts Completely indistinguishable Completely distinguishable Normalized counts Path delay ( ) Path delay ( ) Y-S. Ra et al., PNAS 110, 1227 (2013) Saroosh Shabbir,Gunnar Bj¨ork Interferometric signatures June 3, 2014 32 / 38
- 34. Distinguishability transitions Normalized counts Completely indistinguishable Completely distinguishable Normalized counts Path delay ( ) Path delay ( ) Y-S. Ra et al., PNAS 110, 1227 (2013) Saroosh Shabbir,Gunnar Bj¨ork Interferometric signatures June 3, 2014 33 / 38
- 35. Distinguishability transitions Normalized counts Completely indistinguishable Completely distinguishable Normalized counts Path delay ( ) Path delay ( ) Y-S. Ra et al., PNAS 110, 1227 (2013) Non-monotonic quantum to classical transi�on? Saroosh Shabbir,Gunnar Bj¨ork Interferometric signatures June 3, 2014 34 / 38
- 36. Distinguishability transitions Normalized counts Completely indistinguishable Completely distinguishable Path delay ( ) G. Björk, S. Shabbir, New J. Phys. 16, 013006 (2014) Coincidence detec�on window projects the output onto In fact, one could write projectors for single photon and classical states that also show non-monotonic behaviour. Saroosh Shabbir,Gunnar Bj¨ork Interferometric signatures June 3, 2014 35 / 38
- 37. Distinguishability transitions Normalized counts Completely indistinguishable Completely distinguishable Path delay ( ) G. Björk, S. Shabbir, New J. Phys. 16, 013006 (2014) Coincidence detec�on window projects the output onto In fact, one could write projectors for single photon and classical states that also show non-monotonic behaviour. Non-monotonic projec�on probabili�es as a func�on of dis�nguishability do not signal quantum to classical transi�on. Saroosh Shabbir,Gunnar Bj¨ork Interferometric signatures June 3, 2014 36 / 38
- 38.
- 39. Acknowledgements Gunnar Björk Marcin Swillo Thank you! Saroosh Shabbir,Gunnar Bj¨ork Interferometric signatures June 3, 2014 38 / 38