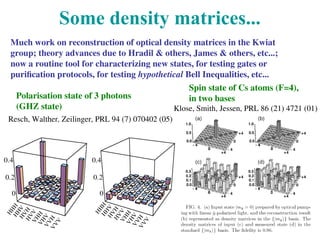
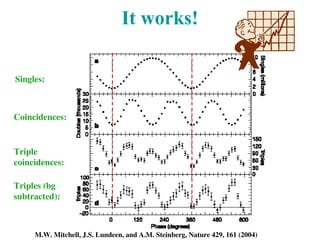
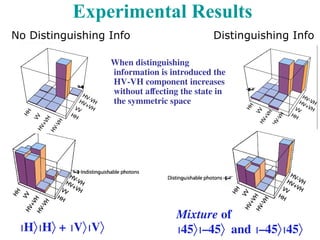
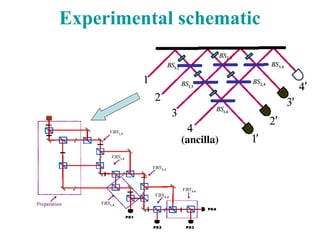
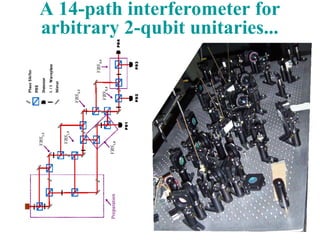
The document discusses advancements in quantum measurements, particularly focusing on real-world applications involving photons and atoms. It covers various measurement techniques, including weak and interaction-free measurements, along with their implications for quantum computing and state discrimination. Additionally, it highlights the significance of understanding quantum information, measurement resolution, and experimental setups to optimize quantum error correction methods.

1. Aephraim M. Steinberg
Centre for Q. Info. & Q. Control
Institute for Optical Sciences
Dept. of Physics, U. of Toronto
Real-World Quantum Measurements:
Fun With Photons and Atoms
CAP 2006, Brock University

2. QuickTime™ and aTIFF (Uncompressed) decompressorare needed to see this picture.
DRAMATIS PERSONÆ
Toronto quantum optics & cold atoms group:
Postdocs: Morgan Mitchell ( ICFO)
Matt Partlow An-Ning Zhang
Optics: Rob Adamson Kevin Resch(Zeilinger  )

Lynden(Krister) Shalm Masoud Mohseni (Lidar)
Xingxing Xing Jeff Lundeen (Walmsley)
Atoms: Jalani Fox (...Hinds) Stefan Myrskog (Thywissen)
Ana Jofre(Helmerson) Mirco Siercke
Samansa Maneshi Chris Ellenor
Rockson Chang Chao Zhuang
Current ug’s: Shannon Wang, Ray Gao, Sabrina Liao, Max Touzel, Ardavan Darabi
Some helpful theorists:
Daniel Lidar, János Bergou, Pete Turner, John Sipe, Paul Brumer, Howard Wiseman, Michael Spanner,...

3. The 3 quantum computer scientists:
see nothing (must avoid "collapse"!)
hear nothing (same story)
say nothing (if any one admits this thing
is never going to work,
that's the end of our
funding!)
Quantum Computer Scientists

4. OUTLINE
The grand unified theory of physics talks:
“Never underestimate the pleasure people
get from being told something they already know.”
Beyond the standard model:
“If you don’t have time to explain something
well, you might as well explain lots of things poorly.”

5. OUTLINE
Measurement: this is not your father’s observable!
• {Forget about projection / von Neumann}
• “Generalized” quantum measurement
• Weak measurement (postselected quantum systems)
• “Interaction-free” measurement, ...
• Quantum state & process tomography
• Measurement as a novel interaction (quantum logic)
• Quantum-enhanced measurement
• Tomography given incomplete information
• {and many more}

6. Distinguishing the indistinguishable...
1

7. How to distinguish non-orthogonal
states optimally
Use generalized (POVM) quantum measurements.
[see, e.g., Y. Sun, J. Bergou, and M. Hillery, Phys.
Rev. A 66, 032315 (2002).]
The view from the laboratory:
A measurement of a two-state system can only
yield two possible results.
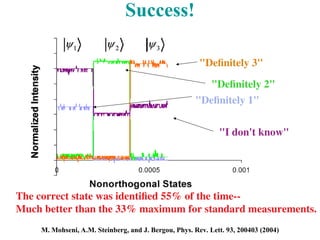
If the measurement isn't guaranteed to succeed, there
are three possible results: (1), (2), and ("I don't know").
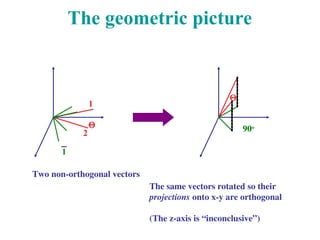
Therefore, to discriminate between two non-orth.
states, we need to use an expanded (3D or more)
system. To distinguish 3 states, we need 4D or more.
H-polarized photon 45o-polarized photon
vs.

8. 
The geometric picture
Two non-orthogonal vectors
The same vectors rotated so their
projections onto x-y are orthogonal
(The z-axis is “inconclusive”)
90o

1
2
1

9. But a unitary transformation in a 4D space produces:
…and these states can be distinguished with certainty
up to 55% of the time
A test case
Consider these three non-orthogonal states:
Projective measurements can distinguish these states
with certainty no more than 1/3 of the time.
(No more than one member of an orthonormal basis is orthogonal
to two of the above states, so only one pair may be ruled out.)

10. Experimental schematic
(ancilla)

11. A 14-path interferometer for
arbitrary 2-qubit unitaries...

12. Success!
The correct state was identified 55% of the time--
Much better than the 33% maximum for standard measurements.
"I don't know"
"Definitely 3"
"Definitely 2"
"Definitely 1"
M. Mohseni, A.M. Steinberg, and J. Bergou, Phys. Rev. Lett. 93, 200403 (2004)

13. Can we talk about what goes on behind closed doors?
(“Postselection” is the big new buzzword in QIP...
but how should one describe post-selected states?)

14. Conditional measurements
(Aharonov, Albert, and Vaidman)
Prepare a particle in |i> …try to "measure" some observable A…
postselect the particle to be in |f>
Does <A> depend more on i or f, or equally on both?
Clever answer: both, as Schrödinger time-reversible.
Conventional answer: i, because of collapse.
i
i f
f
Measurement
of A
Reconciliation: measure A "weakly."
Poor resolution, but little disturbance.
…. can be quite odd …
i
f
i
A
f
A =
w
AAV, PRL 60, 1351 ('88)

15. Predicting the past...
A+B
What are the odds that the particle
was in a given box (e.g., box B)?
B+C
A+B
It had to be in B, with 100% certainty.

16. Consider some redefinitions...
In QM, there's no difference between a box and any other state
(e.g., a superposition of boxes).
What if A is really X + Y and C is really X - Y?
A + B
= X+B+Y
B + C =
X+B-Y
X Y

17. A redefinition of the redefinition...
X + B'
= X+B+Y
X + C' =
X+B-Y
X Y
So: the very same logic leads us to conclude the
particle was definitely in box X.

18. The Rub

19. A (von Neumann) Quantum
Measurement of A
Well-resolved states
System and pointer become entangled
Decoherence / "collapse"
Large back-action
Initial State of Pointer
x x
Hint=gApx
System-pointer
coupling
Final Pointer Readout

20. A Weak Measurement of A
Poor resolution on each shot.
Negligible back-action (system & pointer separable)
Mean pointer shift is given by <A>wk.
Hint=gApx
System-pointer
coupling
x
Initial State of Pointer
x
Final Pointer Readout
Need not lie within spectrum of A, or even be real...

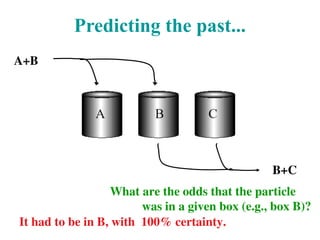
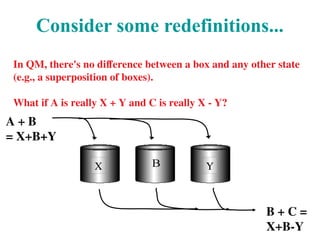
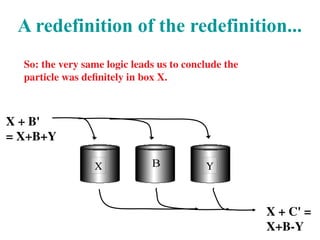
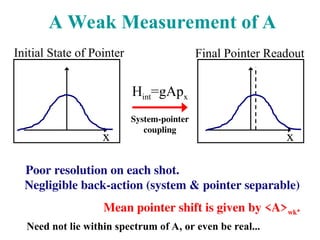
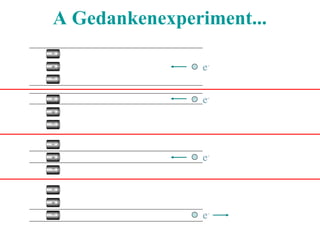
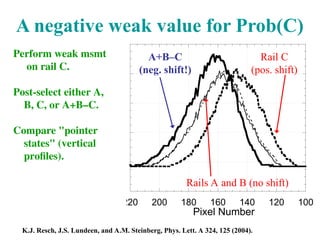
21. The 3-box problem: weak msmts
Prepare a particle in a symmetric superposition of
three boxes: A+B+C.
Look to find it in this other superposition:
A+B-C.
Ask: between preparation and detection, what was
the probability that it was in A? B? C?
Questions:
were these postselected particles really all in A and all in B?
can this negative "weak probability" be observed?
PA = < |A><A| >wk = (1/3) / (1/3) = 1
PB = < |B><B| >wk = (1/3) / (1/3) = 1
PC = < |C><C|>wk = (-1/3) / (1/3) = 1.
i
f
i
A
f
A =
w
[Aharonov & Vaidman, J. Phys. A 24, 2315 ('91)]

22. A Gedankenexperiment...
e-
e-
e-
e-

23. 0.4
0.6
0.8
1
1.2
1.4
100
120
140
160
180
200
220
I
n
t
e
n
s
i
t
y
(
a
r
b
i
t
Pixel Number
Rails A and B (no shift)
Rail C
(pos. shift)
A+B–C
(neg. shift!)
A negative weak value for Prob(C)
Perform weak msmt
on rail C.
Post-select either A,
B, C, or A+B–C.
Compare "pointer
states" (vertical
profiles).
K.J. Resch, J.S. Lundeen, and A.M. Steinberg, Phys. Lett. A 324, 125 (2004).

24. Seeing without looking
2a
QuickTime™ and a
TIFF (Uncompressed) decompresso
are needed to see this picture.
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.

25. Problem:
Consider a collection of bombs so sensitive that
a collision with any single particle (photon, electron, etc.)
is guarranteed to trigger it.
Suppose that certain of the bombs are defective,
but differ in their behaviour in no way other than that
they will not blow up when triggered.
Is there any way to identify the working bombs (or
some of them) without blowing them up?
" Quantum seeing in the dark "
(AKA: The Elitzur-Vaidman bomb experiment)
A. Elitzur, and L. Vaidman, Found. Phys. 23, 987 (1993)
P.G. Kwiat, H. Weinfurter, and A. Zeilinger, Sci. Am. (Nov., 1996)
BS1
BS2
D
C
Bomb absent:
Only detector C fires
Bomb present:
"boom!" 1/2
C 1/4
D 1/4
The bomb must be there... yet
my photon never interacted with it.

26. BS1-
e-
BS2-
O-
C-
D-
I-
BS1+
BS2+
I+
e+
O+
D+
C+
W
Outcome Prob
D+ and C- 1/16
D- and C+ 1/16
C+ and C- 9/16
D+ and D- 1/16
Explosion 4/16
Hardy's Paradox
(for Elitzur-Vaidman “interaction-free measurements”)
D- –> e+ was in
D+D- –> ?
But … if they were
both in, they
should
have annihilated!
D+ –> e- was in

27. Probabilities e- in e- out
e+ in 1
e+ out 0
1 0
0 1
1 1
But what can we say about where the particles
were or weren't, once D+ & D– fire?
In fact, this is precisely what Aharonov et al.’s weak measurement
formalism predicts for any sufficiently gentle attempt to “observe”
these probabilities...

28. N(I-
) N(O
)
N(I+
) 0 1 1
N(O+
) 1 1 0
1 0
0.039±0.023
0.925±0.024
0.087±0.021
0.758±0.083
0.721±0.074
N(O+
)
0.882±0.015
0.663±0.083
0.243±0.068
N(I+
)
N(O
)
N(I-
)
Experimental Weak Values (“Probabilities”?)
Ideal Weak Values
Weak Measurements in Hardy’s Paradox

29. Quantum tomography: what & why?
3
1. Characterize unknown quantum states & processes
2. Compare experimentally designed states & processes to design goals
3. Extract quantities such as fidelity / purity / tangle
4. Have enough information to extract any quantities defined in the future!
• or, for instance, show that no Bell-inequality could be violated
5. Learn about imperfections / errors in order to figure out how to
• improve the design to reduce imperfections
• optimize quantum-error correction protocols for the system

30. Quantum Information
What's so great about it?

31. What makes a computer quantum?
If a quantum "bit" is described by two numbers:
|Ψ> = c0|0> + c1|1>,
then n quantum bits are described by 2
n coeff's:
|Ψ> = c00..0|00..0>+c00..1|00..1>+...c11..1|11..1>;
this is exponentially more information than the 2n coefficients
would take to describe n independent (e.g., classical) bits.
It is also exponentially sensitive to decoherence.
Photons are ideal carriers of quantum information-- they
can be easily produced, manipulated, and detected, and
don't interact significantly with the environment. They
are already used to transmit quantum-cryptographic
information through fibres under Lake Geneva, and soon
through the air up to satellites.
across the Danube
We need to understand the nature of quantum information itself.
How to characterize and compare quantum states?
How to most fully describe their evolution in a given system?
How to manipulate them?
The danger of errors & decoherence grows exponentially with system size.
The only hope for QI is quantum error correction.
We must learn how to measure what the system is doing, and then correct it.
(One partial answer...)

32. Density matrices and superoperators
One photon: H or V.
State: two coefficients
( )
CH
CV
( )
CHH
CHV
CVH
CVV
Density matrix: 2x2=4 coefficients
Measure
intensity of horizontal
intensity of vertical
intensity of 45o
intensity of RH circular.
Propagator (superoperator): 4x4 = 16 coefficients.
Two photons: HH, HV, VH, VV, or any superpositions.
State has four coefficients.
Density matrix has 4x4 = 16 coefficients.
Superoperator has 16x16 = 256 coefficients.

33. Some density matrices...
Resch, Walther, Zeilinger, PRL 94 (7) 070402 (05)
Klose, Smith, Jessen, PRL 86 (21) 4721 (01)
Polarisation state of 3 photons
(GHZ state)
Spin state of Cs atoms (F=4),
in two bases
Much work on reconstruction of optical density matrices in the Kwiat
group; theory advances due to Hradil & others, James & others, etc...;
now a routine tool for characterizing new states, for testing gates or
purification protocols, for testing hypothetical Bell Inequalities, etc...

34. QuickTime™ and a
Photo - JPEG decompressor
are needed to see this picture.
Wigner function of atoms’ vibrational
quantum state in optical lattice
J.F. Kanem, S. Maneshi, S.H. Myrskog, and A.M. Steinberg, J. Opt. B. 7, S705 (2005)

35. Superoperator after transformation
to correct polarisation rotations:
Residuals allow us to estimate
degree of decoherence and
other errors.
Superoperator provides information
needed to correct & diagnose operation
Measured superoperator,
in Bell-state basis:
Leading Kraus operator allows
us to determine unitary error.
(expt) (predicted)
M.W. Mitchell, C.W. Ellenor, S. Schneider, and A.M. Steinberg, Phys. Rev. Lett. 91 , 120402 (2003)

36. QPT of QFT
Weinstein et al., J. Chem. Phys. 121, 6117 (2004)
To the trained eye, this is a Fourier transform...

37. The status of quantum cryptography

38. Measurement as a tool:
Post-selective operations for the construction of
novel (and possibly useful) entangled states...
4a

39. Theory: H. Lee et al., Phys. Rev. A 65, 030101 (2002); J. Fiurásek, Phys. Rev. A 65, 053818 (2002)
Highly number-entangled states
("low-noon" experiment).
Important factorisation:
=
+
A "noon" state
A really odd beast: one 0o
photon,
one 120o
photon, and one 240o
photon...
but of course, you can't tell them apart,
let alone combine them into one mode!
States such as |n,0> + |0,n> ("noon" states) have been proposed for
high-resolution interferometry – related to "spin-squeezed" states.

40. Trick #1
Okay, we don't even have single-photon sources*
.
But we can produce pairs of photons in down-conversion, and
very weak coherent states from a laser, such that if we detect
three photons, we can be pretty sure we got only one from the
laser and only two from the down-conversion...
SPDC
laser
|0> +  |2> + O(2
)
|0> +  |1> + O(2
)
 |3> + O(3
) + O(2
)
+ terms with <3 photons
*
But we’re working on it (collab. with Rich Mirin’s quantum-dot group at NIST)

41. How to combine three non-orthogonal photons into one spatial mode?
Postselective nonlinearity
Postselective nonlinearity
Yes, it's that easy! If you see three photons
out one port, then they all went out that port.
"mode-mashing"

42. -
+ ei3φ
HWP
QWP
Phase
shifter
PBS
DC
photons PP
Dark ports
Ti:sa
to
analyzer
The basic optical scheme

43. It works!
Singles:
Coincidences:
Triple
coincidences:
Triples (bg
subtracted):
M.W. Mitchell, J.S. Lundeen, and A.M. Steinberg, Nature 429, 161 (2004)

44. Complete characterisation
when you have incomplete information
4b
4b

45. Fundamentally Indistinguishable
vs.
Experimentally Indistinguishable
But what if when we combine our photons,
there is some residual distinguishing information:
some (fs) time difference, some small spectral
difference, some chirp, ...?
This will clearly degrade the state – but how do
we characterize this if all we can measure is
polarisation?

46. Quantum State Tomography
{ }
2
1
2
1
2
1
2
1 ,
,
, V
V
V
H
H
V
H
H
Distinguishable Photon
Hilbert Space
{ }
, ,
HH HV VH VV
+
{ }
2 ,0 , 1 ,1 , 0 ,2
H V H V H V
Indistinguishable
Photon Hilbert Space
?
Yu. I. Bogdanov, et al
Phys. Rev. Lett. 93, 230503 (2004)
If we’re not sure whether or not the particles are distinguishable,
do we work in 3-dimensional or 4-dimensional Hilbert space?
If the latter, can we make all the necessary measurements, given
that we don’t know how to tell the particles apart ?

47. The sections of the density matrix labelled “inaccessible” correspond to
information about the ordering of photons with respect to inaccessible
degrees of freedom.
The Partial Density Matrix
Inaccessible
information
Inaccessible
information
ρHH,HH ρHV +VH,HH ρVV ,HH
ρHH,HV +VH ρHV +VH,HV +VH ρVV ,HV +VH
ρHH,VV ρHV +VH,VV ρVV ,VV
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
ρHV −VH,HV −VH
( )
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
The answer: there are only 10 linearly independent parameters which
are invariant under permutations of the particles. One example:
(For n photons, the # of parameters scales as n3
, rather than 4n
)
R.B.A. Adamson, L.K. Shalm, M.W. Mitchell, and A.M. Steinberg, quant-ph/0601134

48. When distinguishing
information is introduced the
HV-VH component increases
without affecting the state in
the symmetric space
Experimental Results
No Distinguishing Info Distinguishing Info
HH + VV
Mixture of
45–45 and –4545

49. The moral of the story
1. Post-selected systems often exhibit surprising behaviour which
can be probed using weak measurements.
2. Post-selection can also enable us to generate novel “interactions”
(KLM proposal for quantum computing), and for instance to
produce useful entangled states.
3. POVMs, or generalized quantum measurements, are in some
ways more powerful than textbook-style projectors
4. Quantum process tomography may be useful for characterizing
and "correcting" quantum systems (ensemble measurements).
5. A modified sort of tomography is possible on “practically
indistinguishable” particles
QuickTime™ and a
YUV420 codec decom
are needed to see this
Predicted Wigner-Poincaré
function for a variety of
“triphoton states” we are
starting to produce: