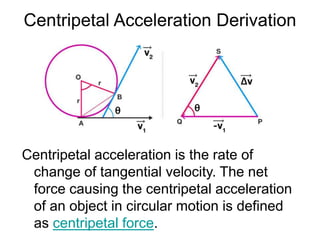
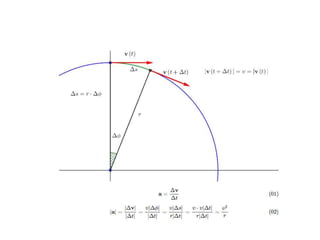
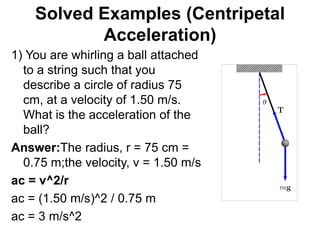
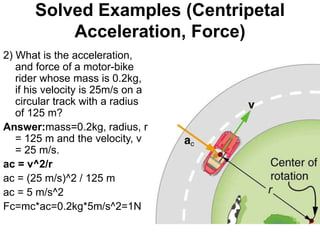
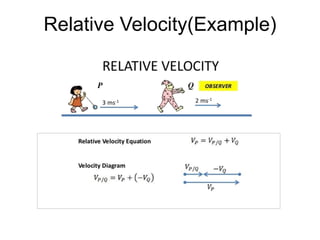
The document discusses concepts related to circular and rotational motion including: 1) Relative motion velocity refers to the velocity of an object relative to another object that may be stationary, moving at the same or different speeds, or moving in opposite directions. 2) Uniform circular motion involves an object moving in a circle at constant speed, requiring centripetal acceleration towards the center to change its direction. 3) In non-uniform circular motion, both centripetal and tangential acceleration are present as the angular velocity or speed changes. The total linear acceleration is the vector sum of these two accelerations.

1. Second PPT
HARSHIT OMAR

2. Horizontally launched particle
with its velocity’s x and y-
components?

3. Projectile launched at angle ‘theta’

4. Projectiles launched to/from Height

5. Projectile Motion on an inclined
plane

6. Relative velocity in 2 Dimension
• The concept of relative motion velocity in a plane is
quite similar to the whole concept of relative velocity in
a straight line.
• What is Relative Motion Velocity?
The relative motion velocity refers to an object which is
relative to some other object that might be stationary,
moving with the same velocity, or moving slowly, moving
with higher velocity or moving in the opposite direction.
The wide concept of relative velocity can be very easily
extended for motion along a straight line, to include
motion in a plane or either in three dimensions.

7. Relative Velocity(Example)

10. Solved Problems on Relative
Velocity

12. Ques) A boat heads due North across a river with a speed of Vbr = 10
km/h relative to the water. The river has a speed of VrE = 5 km/h due
East, relative to Earth. Determine the velocity of the boat relative to
Earth VbE? (that is, the velocity of the boat relative to an observer
watching from the bank of the river).

13. Pictorial Representation of Boat
and Water Problem

14. Accelerating objects are objects which are changing their
velocity - either the speed (i.e., magnitude of the velocity
vector) or the direction. An object undergoing uniform
circular motion is moving with a constant speed.
Nonetheless, it is accelerating due to its change in
direction. The direction of the acceleration is inwards.
• Uniform circular motion can be described
as the motion of an object in a circle at a
constant speed. As an object moves in a
circle, it is constantly changing its
direction. At all instances, the object is
moving tangent to the circle. Since the
direction of the velocity vector is the
same as the direction of the object's
motion, the velocity vector is directed
tangent to the circle as well.
Uniform Circular Motion

15. Angular Motion Variables
• The equivalent variables for
rotation are angular
displacement ‘theta’ (Unit:
radians), angular velocity ‘w’
(Unit: radians/second),
and angular acceleration. All
the angular variables are
related to the straight-line
variables by a factor of ‘r’,
radius. The net centripetal
force is said to be an inward
force towards center.

16. Linear velocity & Angular velocity

17. Solved Examples

18. Solved Examples

19. How angular frequency and
regular frequency are related?
• Angular frequency ω (in
radians per second), is
larger than frequency ν
(in cycles per second,
also called Hz), by a
factor of 2π. Angular
frequency (in radians) is
larger than regular
frequency (in Hz) by a
factor of 2π:
• ω = 2πf
• Hence, 1 Hz ≈ 6.28
rad/sec. Since 2π radians
= 360°, 1 radian ≈ 57.3°.

20. Centripetal Acceleration Formula
• Centripetal acceleration of
an object in a circle of radius
‘r’ at a speed ‘v’ is
• Centripetal
acceleration=v^2/r
• So, rate of change of
tangential velocity is called as
the centripetal acceleration.
Centripetal acceleration is
greater at high speeds and in
sharp curves (smaller radius),
as you have noticed when
driving a car.

21. Centripetal Acceleration Derivation
Centripetal acceleration is the rate of
change of tangential velocity. The net
force causing the centripetal acceleration
of an object in circular motion is defined
as centripetal force.

23. Solved Examples (Centripetal
Acceleration)
1) You are whirling a ball attached
to a string such that you
describe a circle of radius 75
cm, at a velocity of 1.50 m/s.
What is the acceleration of the
ball?
Answer:The radius, r = 75 cm =
0.75 m;the velocity, v = 1.50 m/s
ac = v^2/r
ac = (1.50 m/s)^2 / 0.75 m
ac = 3 m/s^2

24. Solved Examples (Centripetal
Acceleration, Force)
2) What is the acceleration,
and force of a motor-bike
rider whose mass is 0.2kg,
if his velocity is 25m/s on a
circular track with a radius
of 125 m?
Answer:mass=0.2kg, radius, r
= 125 m and the velocity, v
= 25 m/s.
ac = v^2/r
ac = (25 m/s)^2 / 125 m
ac = 5 m/s^2
Fc=mc*ac=0.2kg*5m/s^2=1N

25. Relating Angular & Regular Motion
Variables
• Centripetal acceleration = (linear
velocity)^2/radius -(eq. 1)
• Linear velocity= angular
velocity/radius -(eq. 2)
Using eq. 1 and eq. 2, we get,
• Centripetal acceleration
= (angular velocity)^2*radius
=w^2*r

26. Solved Examples

27. Solved Examples

28. Relating Angular & Regular Motion
Variables

29. Difference between Linear and
Angular Acceleration
• Linear acceleration is
the translational
acceleration felt by an object.
When linear acceleration is
applied to a body, the entire
body is affected by the
acceleration (or the force) at
the same time.
• Angular accleration is
the rotational acceleration felt
by an object about an axis.
When angular acceleration is
applied to a body, parts of the
body experience acceleration
different from acceleration in
other parts of the body.
• Linear Acceleration=Angular
acceleration*radius

30. Total acceleration in Non-Uniform
Circular Motion
Thus, in uniform circular motion when the angular velocity is
constant and the angular acceleration is zero, we have a linear
acceleration—that is, centripetal acceleration. If non-uniform
circular motion is present, the rotating system has an angular
acceleration, and we have both a linear centripetal acceleration
that is changing as well as a linear tangential acceleration.
where we show the centripetal and tangential accelerations for
uniform and non-uniform circular motion.

31. • The centripetal acceleration is due to the change in the
direction of tangential velocity, whereas the tangential
acceleration is due to any change in the magnitude of
the tangential velocity. The tangential and centripetal
acceleration vectors at and ac are always perpendicular
to each other. To complete this description, we can
assign a total linear acceleration vector to a point on a
rotating rigid body or a particle executing circular motion
at a radius r from a fixed axis. The total linear
acceleration vector a the vector sum of the centripetal
and tangential accelerations,
• a=ac + at
• |a|=√ac^2+at^2

32. Solved Example (Total
Acceleration)

33. Solved Example (Total
Acceleration)