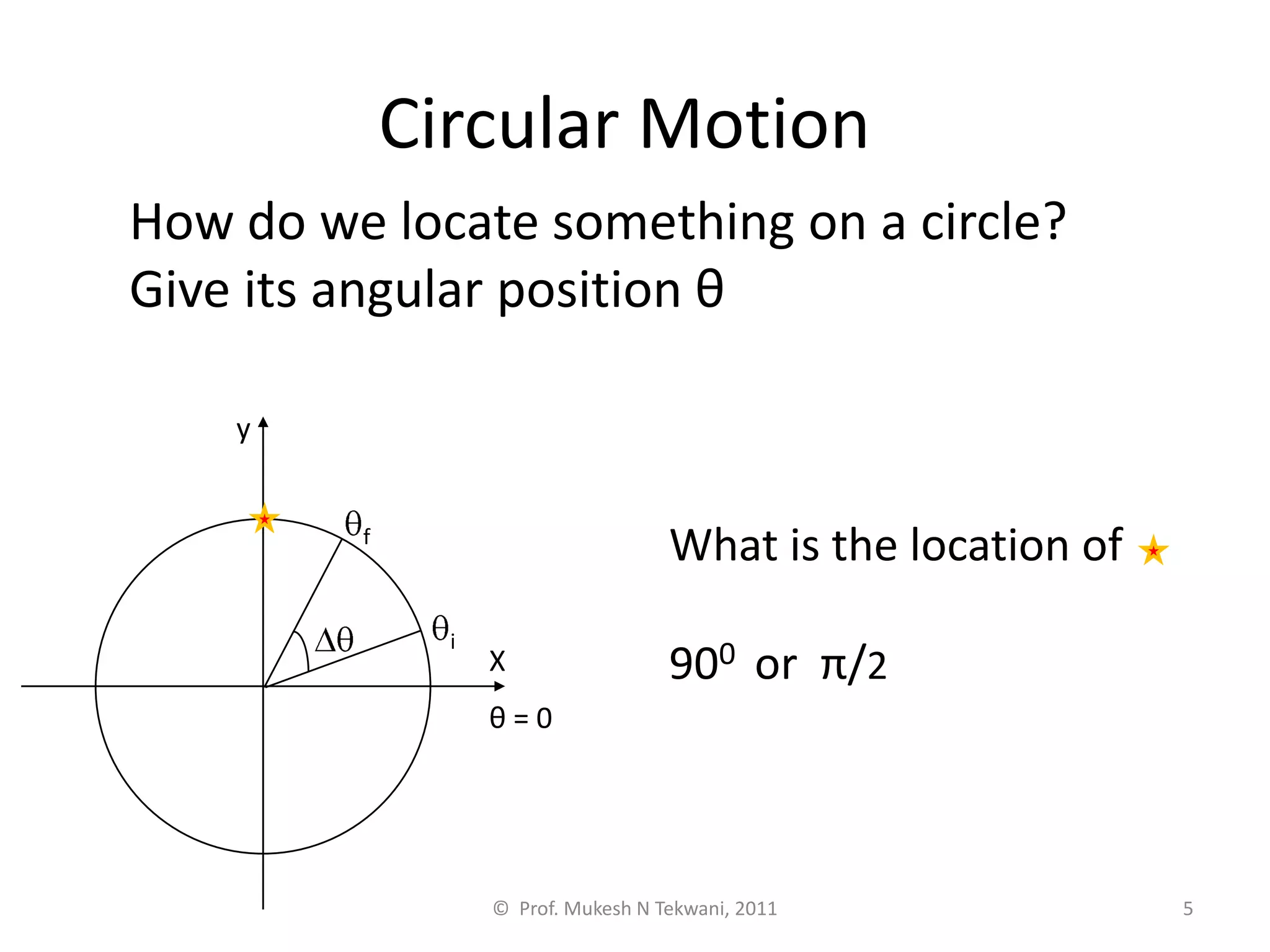
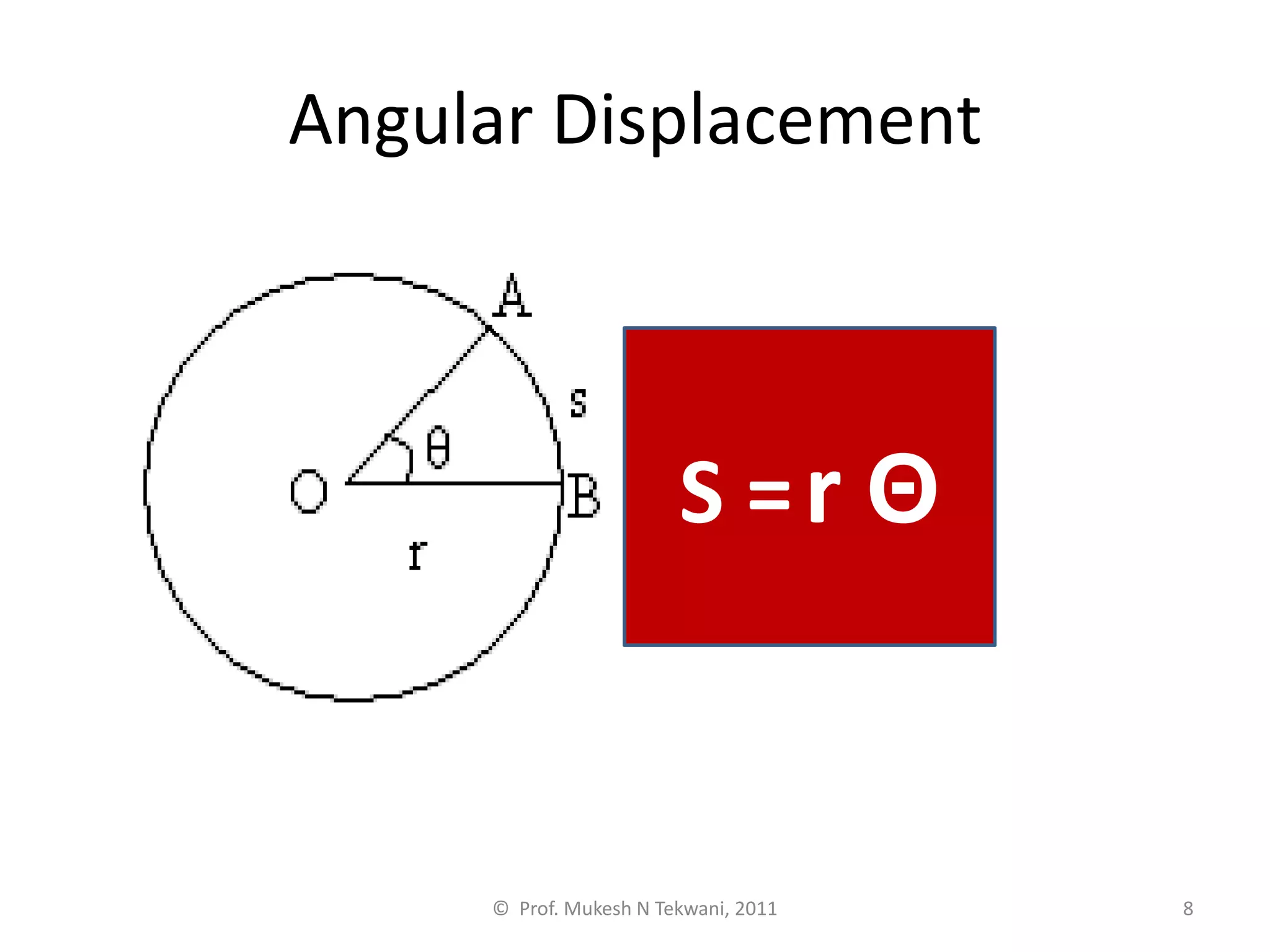
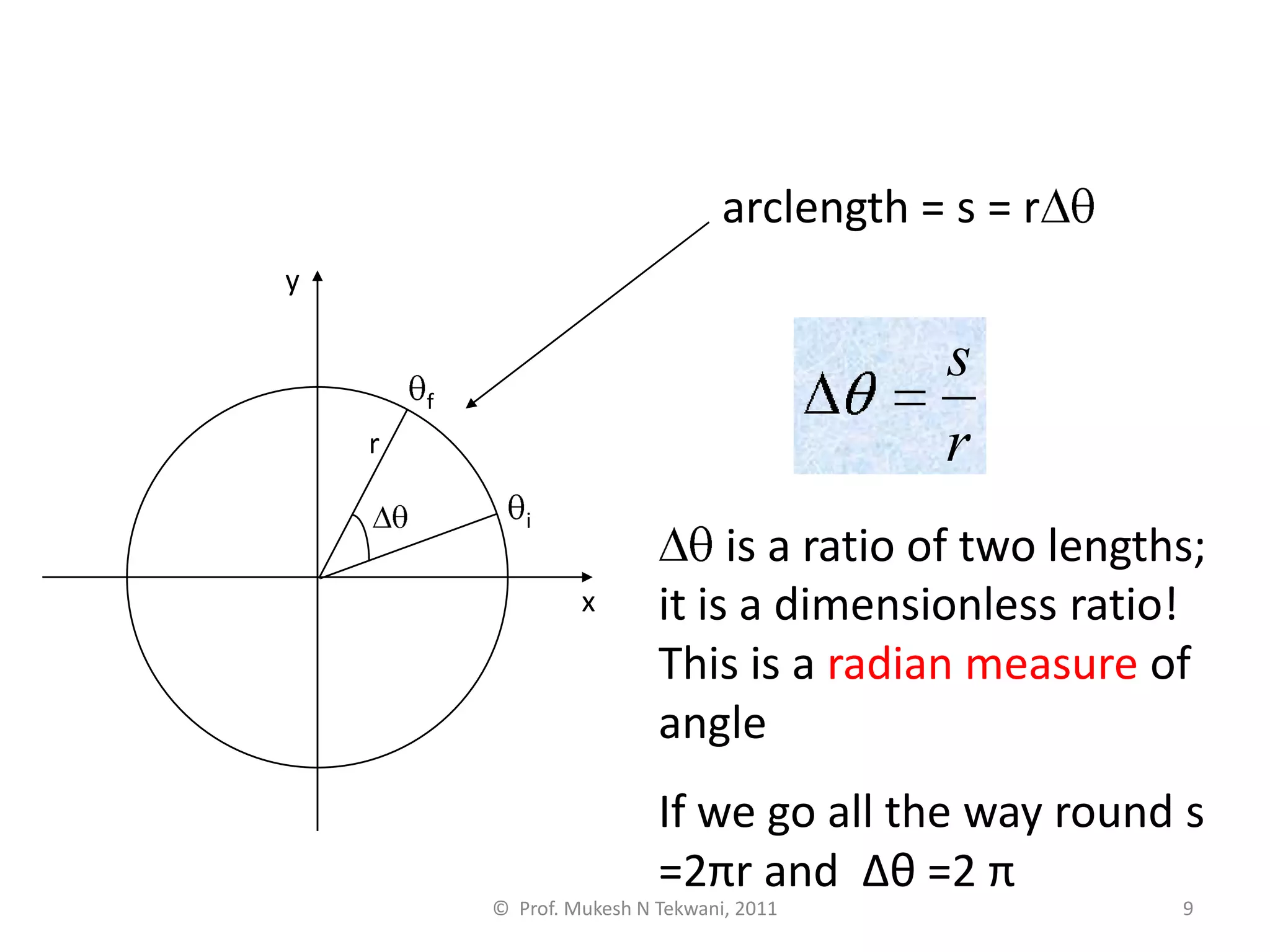
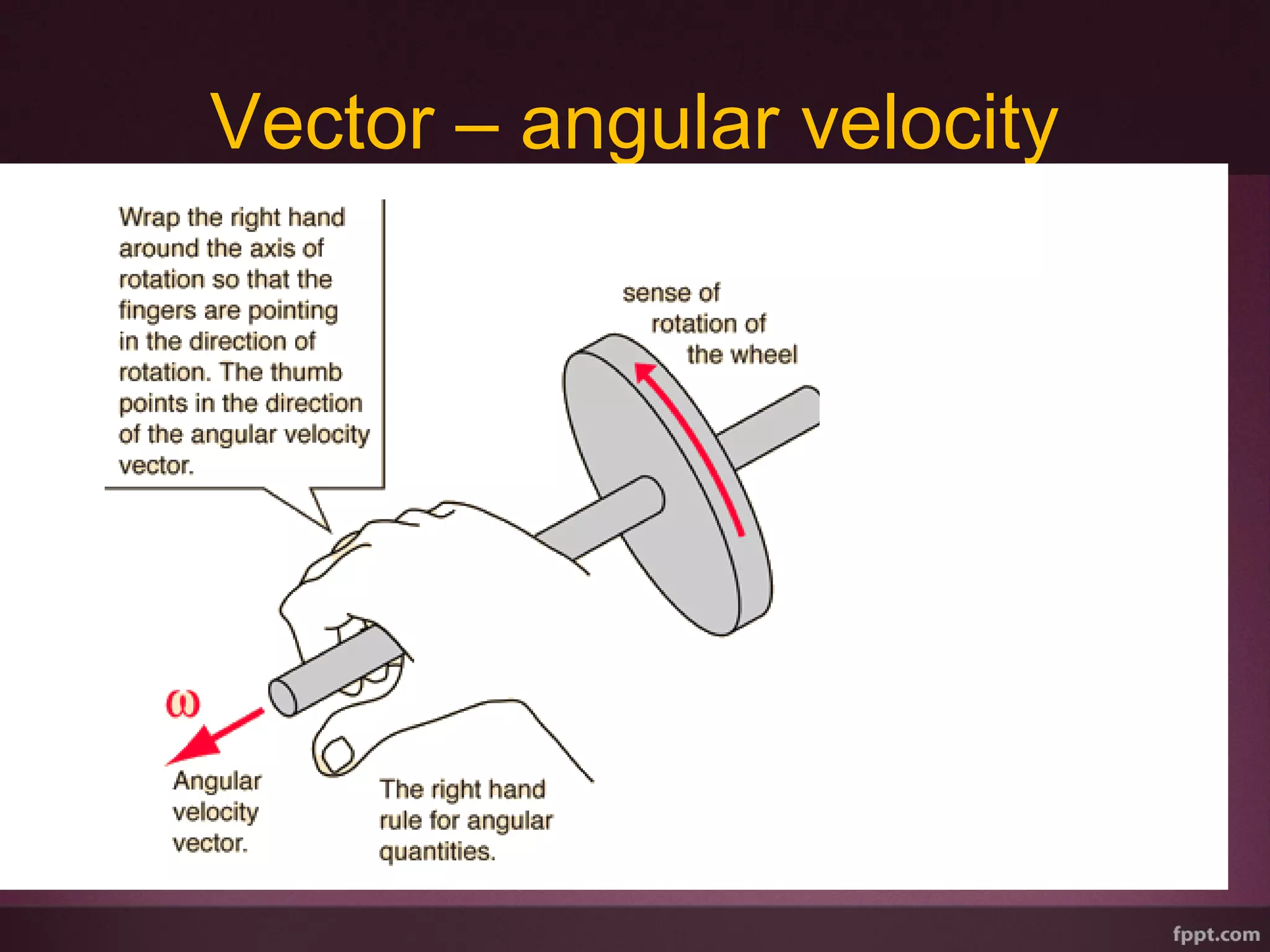
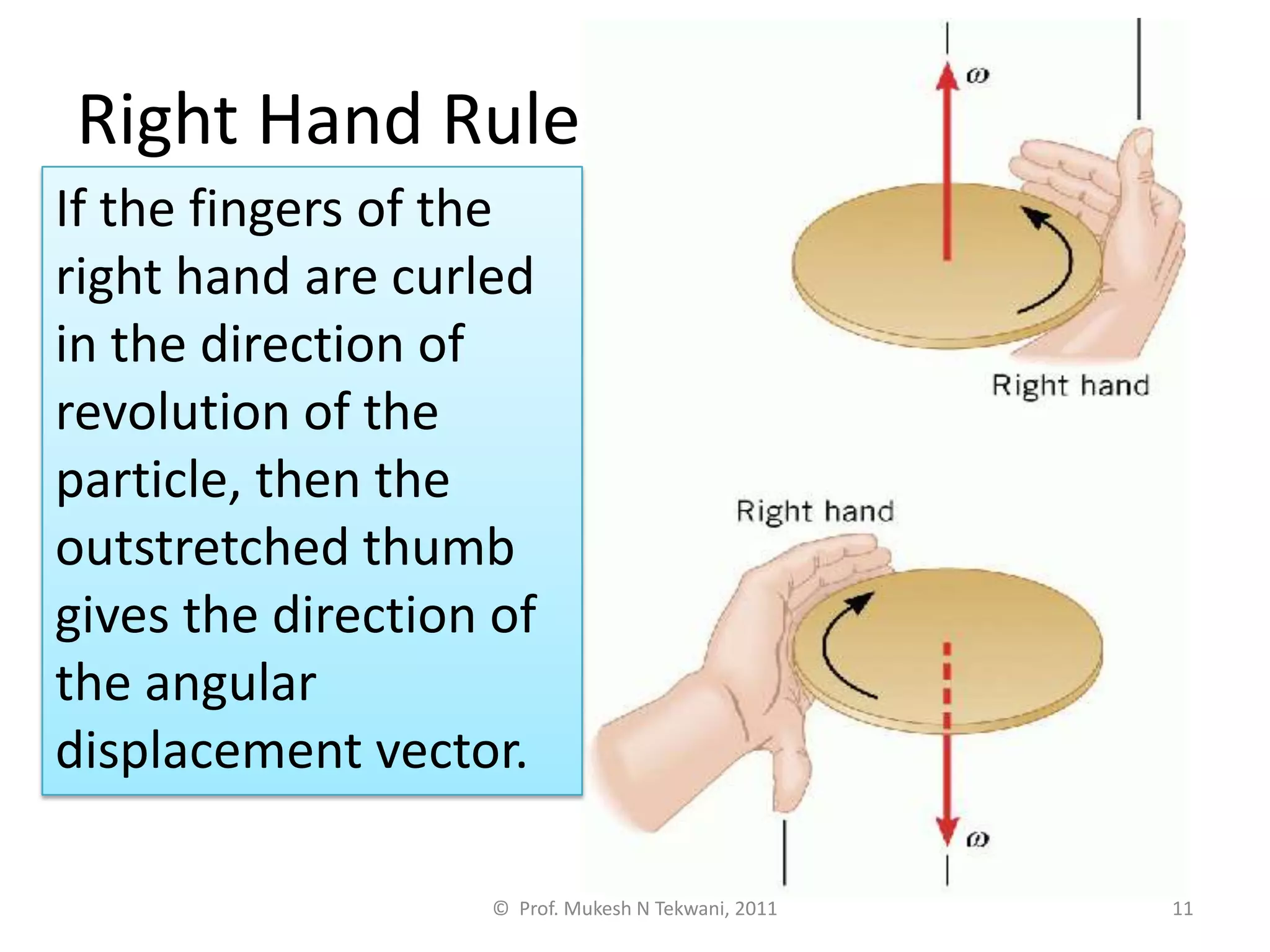
This document discusses circular motion. It defines circular motion as motion along a circular path or arc. Uniform circular motion refers to motion at a constant speed along the path. Angular displacement is defined as the angle described by the radius vector from the initial to final position of an object in circular motion. Angular displacement is measured in radians, with one radian equal to an arc length equal to the radius. Angular velocity refers to the rate of change of the angular displacement and indicates both the magnitude and direction of rotational motion. Centripetal forces are also discussed as providing the inward acceleration needed for circular motion.

1. Circular Motion
2
© Prof. Mukesh N Tekwani, 2011

2. Why study Circular Motion?
• To understand
– Motion of planets
– Motion of electrons around the nucleus
– Motion of giant wheel
– Motion of space stations
– Motion of moon and satellites
3

3. Circular Motion
• It is defined as the motion of a particle along a
complete circle or part of a circle.
• Fore circular motion, it is NOT necessary that
the body should complete a full circle.
• Even motion along arc of a circle is circular
motion
4

4. CONTENTS
• CIRCULAR MOTION
• ANGULAR DISPLACEMENT
• ANGULAR SPEED
• ANGULAR VELOCITY
• CENTRIPETAL FORCES &
ACCELERATION

5. CIRCULAR MOTION
• If an object/ body is moving along a
circular path it is said to be in circular
motion.
• Uniform circular motion : If the object
move with uniform speed along the
circular path, it is said to have uniform
circular motion.

6. Angular displacement
• The angle through which the radius
vector representing the position of a
particle rotates is called angular
displacement
• The change in position of the particle in
a circular path with respect to its centre
is called angular displacement.
• The angular displacement of a body
with respect to a reference line is
denoted as θ.

8. 5
Circular Motion
X
θ = 0
y
i
f
How do we locate something on a circle?
Give its angular position θ
What is the location of
900 or π/2
© Prof. Mukesh N Tekwani, 2011

9. 6
Circular Motion
is the angular position.
Angular displacement:
i
f
Note: angles measured Clockwise (CW) are negative and
angles measured (CCW) are positive. is measured in
radians.
2 radians = 360 = 1 revolution
x
y
i
f
© Prof. Mukesh N Tekwani, 2011

10. Angular Displacement
• Angular displacement is defined as the angle
described by the radius vector
© Prof. Mukesh N Tekwani, 2011 7
a
Initial position of particle is a
Final position of particle is b
Angular displacement in time t is Θ

11. Angular Displacement
© Prof. Mukesh N Tekwani, 2011 8
S =r Θ

12. 9
x
y
i
f
r
arclength = s = r
r
s
is a ratio of two lengths;
it is a dimensionless ratio!
This is a radian measure of
angle
If we go all the way round s
=2πr and Δθ =2 π
© Prof. Mukesh N Tekwani, 2011

13. Angular Displacement Units
• The angular displacement can be
measured in degree.
• But the S.I. Unit for angular displacement
is Radians.
• One radian is defined as the angle
subtended at the centre of a circle by
an arc which is equal to length of the
arc divided by the radius of the circle.

15. Conversion between degree
and radians
• When an object makes through a
complete circle,
• angular displacement in the entire circle
is 3600
= 2π radians
• 1 0
= 2π/ 180
• 1 radian = 180 / 2π degrees

17. Question to check how far you
understood
• By how many degrees does the angular
displacement of the hour hand of a clock
change each hour ?

18. Speed steady , but velocity ?
• An object moving in uniform circular motion is
moving in a circle with a uniform or constant
speed.
• Is it accelerating ?
• Yes, because, it is changing the velocity.
• Since velocity is a vector which has both
magnitude and direction, a change in either the
magnitude or the direction constitutes a change
in the velocity.

19. Angular velocity
• Angular velocity, also called rotational
velocity, is a quantitative expression of the
amount of rotation that a spinning object
undergoes per unit time.

21. Vector – angular velocity

22. Right Hand Rule
© Prof. Mukesh N Tekwani, 2011 11
If the fingers of the
right hand are curled
in the direction of
revolution of the
particle, then the
outstretched thumb
gives the direction of
the angular
displacement vector.