Download as PDF, PPTX
Uploaded bySonarin Cruz
Axiomatic Development of Geometry: An Introduction
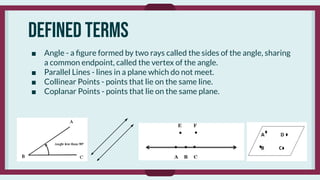
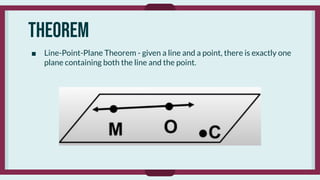
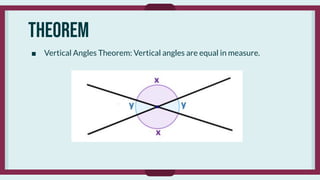
The document describes the key components of an axiomatic system for geometry: - Undefined terms like point, line, and plane that can only be described, not defined. - Defined terms with precise definitions like angle, parallel lines, and midpoint. - Axioms/postulates that are accepted as true without proof, such as lines determined by points and planes containing points. - Theorems that are proven true using definitions, axioms, and logical reasoning, such as the Vertical Angles Theorem.
More Related Content
![[FILIPINO 8] - Kaugnayang Lohikal](https://cdn.slidesharecdn.com/ss_thumbnails/filipino8-kaugnayanglohikal-161203130343-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Axiomatic Development of Geometry: An Introduction
![012 euclidean geometry[1]](https://cdn.slidesharecdn.com/ss_thumbnails/012euclideangeometry1-181201153749-thumbnail.jpg?width=640&height=640&fit=bounds)
Axiomatic Development of Geometry: An Introduction
- 1. 07 08 0910 11 12 02 03 04 05 06 17 18 19 20 21 22 13 14 15 16 AXIOMATIC DEVELOPMENT OF GEOMETRY 01
- 2. 07 08 0910 11 12 02 03 04 05 17 18 19 20 21 22 13 14 15 16 It is a system made up undefined terms, defined terms, axioms/postulates, and theorems which are used in proving logical conclusions in geometry. Axiomatic system 06 01
- 3. Undefined terms Defined terms axioms/postulates theorems 0708 09 10 11 12 02 03 04 05 17 18 19 20 21 22 13 14 15 16 06 01
- 4. 07 08 0910 11 12 02 03 04 05 17 18 19 20 21 22 13 14 15 16 Are terms that cannot be defined because they can only be described or illustrated. Undefined terms 06 01 The three undefined terms are point, line and plane.
- 5. 07 08 0910 11 12 02 03 04 05 17 18 19 20 21 22 13 14 15 16 Are terms with a precise and concise definition. defined terms 06 01 A definition is a precise statement or description of the meaning of the term or word so that anyone using it will understand it in the same way. Ex. Parallel lines, angle, midpoint
- 6. defined terms ■ Angle- a figure formed by two rays called the sides of the angle, sharing a common endpoint, called the vertex of the angle. ■ Parallel Lines - lines in a plane which do not meet. ■ Collinear Points - points that lie on the same line. ■ Coplanar Points - points that lie on the same plane.
- 7. 07 08 0910 11 12 02 03 04 05 17 18 19 20 21 22 13 14 15 16 Are statements accepted to be true without proof. Postulates are statement from geometry. Axioms are statement from other sections of mathematics. axioms/postulates 06 01
- 8. postulate ■ Line postulate- for every two points, there is exactly one line that contains both points. ■ Plane postulate - any three noncollinear points lie in at least one plane.
- 9. 07 08 0910 11 12 02 03 04 05 17 18 19 20 21 22 13 14 15 16 Are statements that are proven to be true using definitions, axioms/postulates, and derived using reasoning. theorem 06 01 Proof - a sequence of true facts that are arranged in a logical order.
- 10. theorem ■ Vertical AnglesTheorem: Vertical angles are equal in measure.
- 11. theorem ■ Line-Point-Plane Theorem- given a line and a point, there is exactly one plane containing both the line and the point.
- 12. theorem ■ Proof: ■ PointsM, O and C are non collinear points. By plane postulate, any three noncollinear points lie exactly in one plane. Also, by line postulate, any two points determine a straight line. Therefore, there is exactly one plane containing line MO and point C.