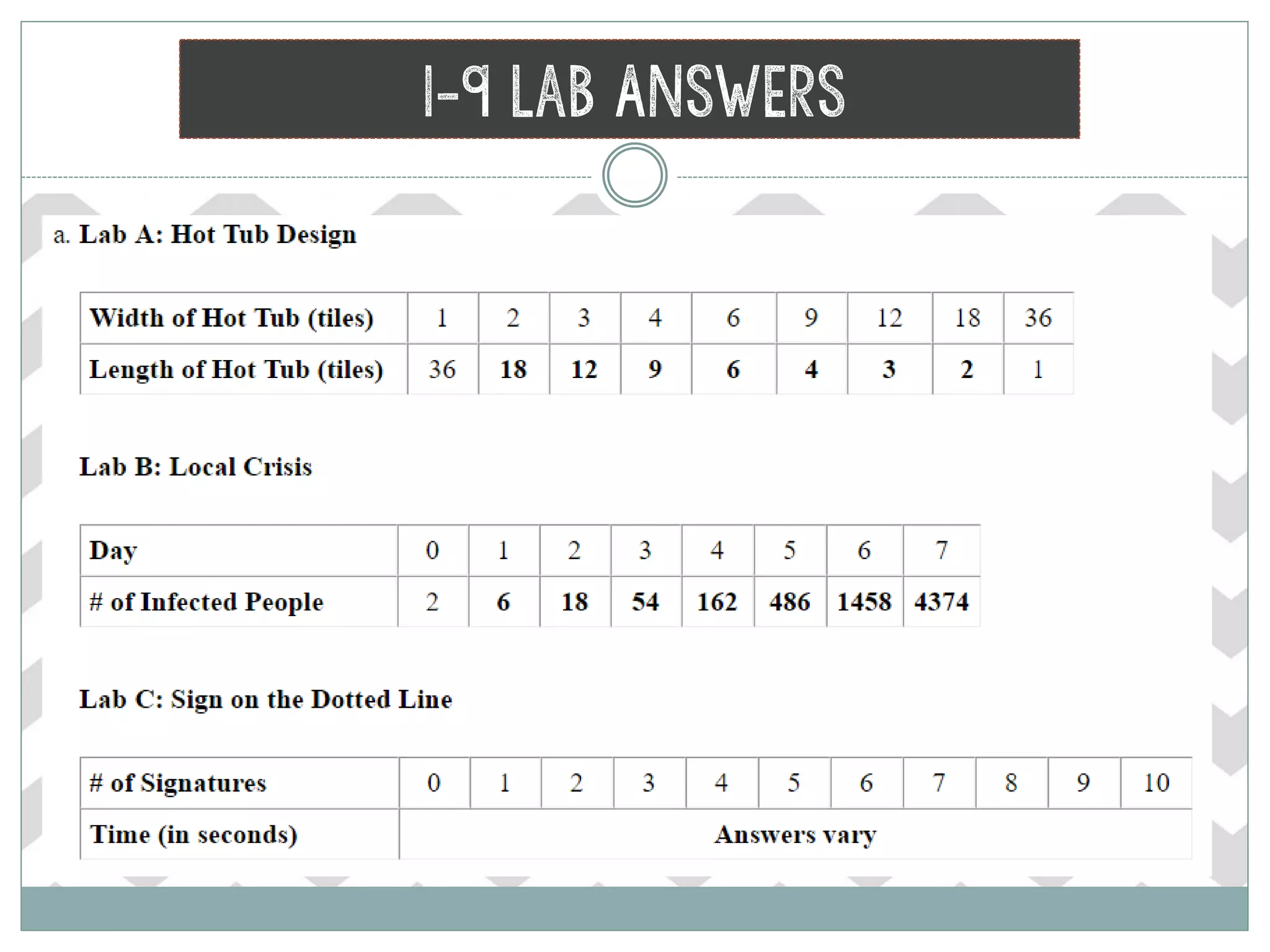
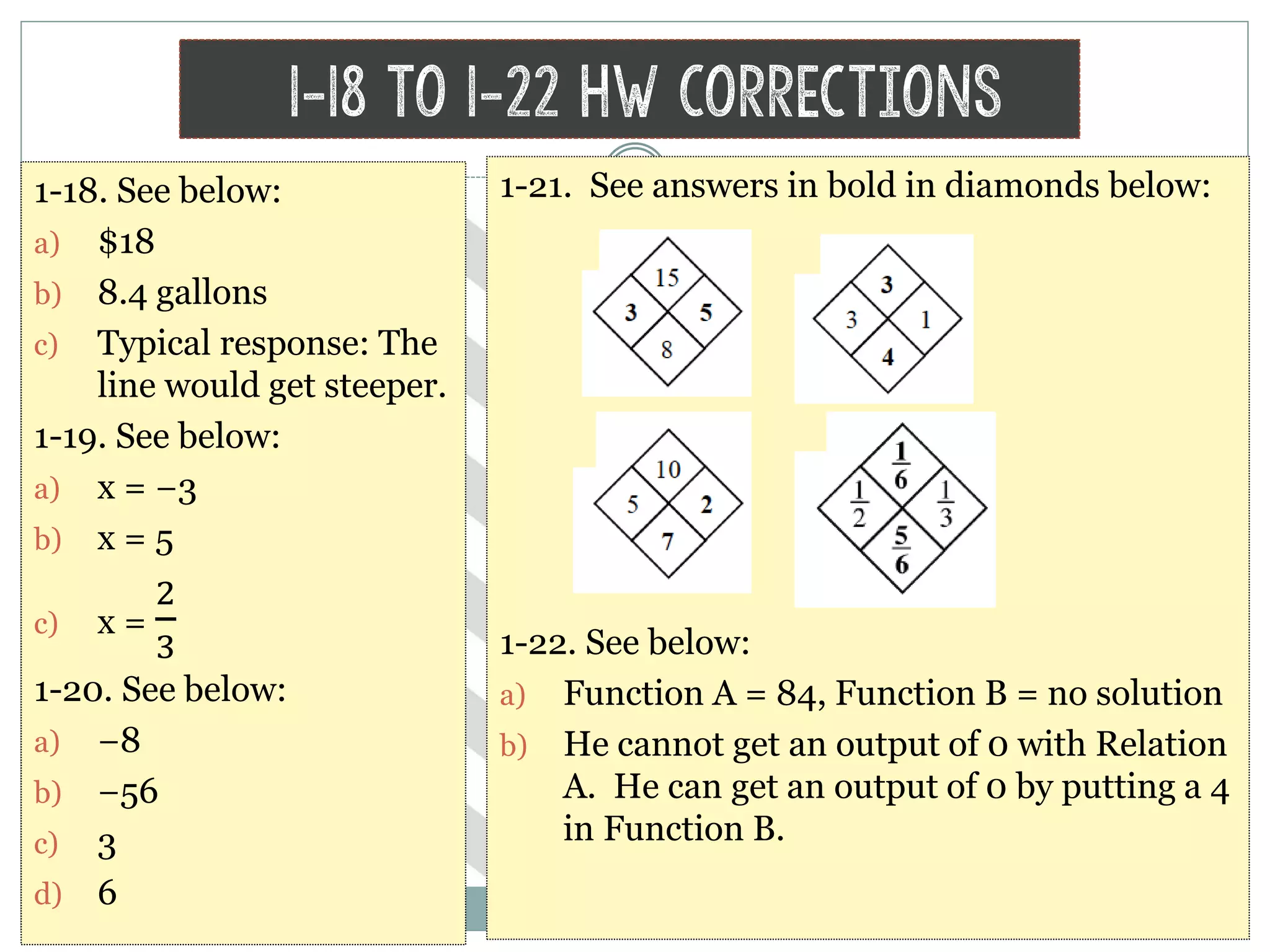
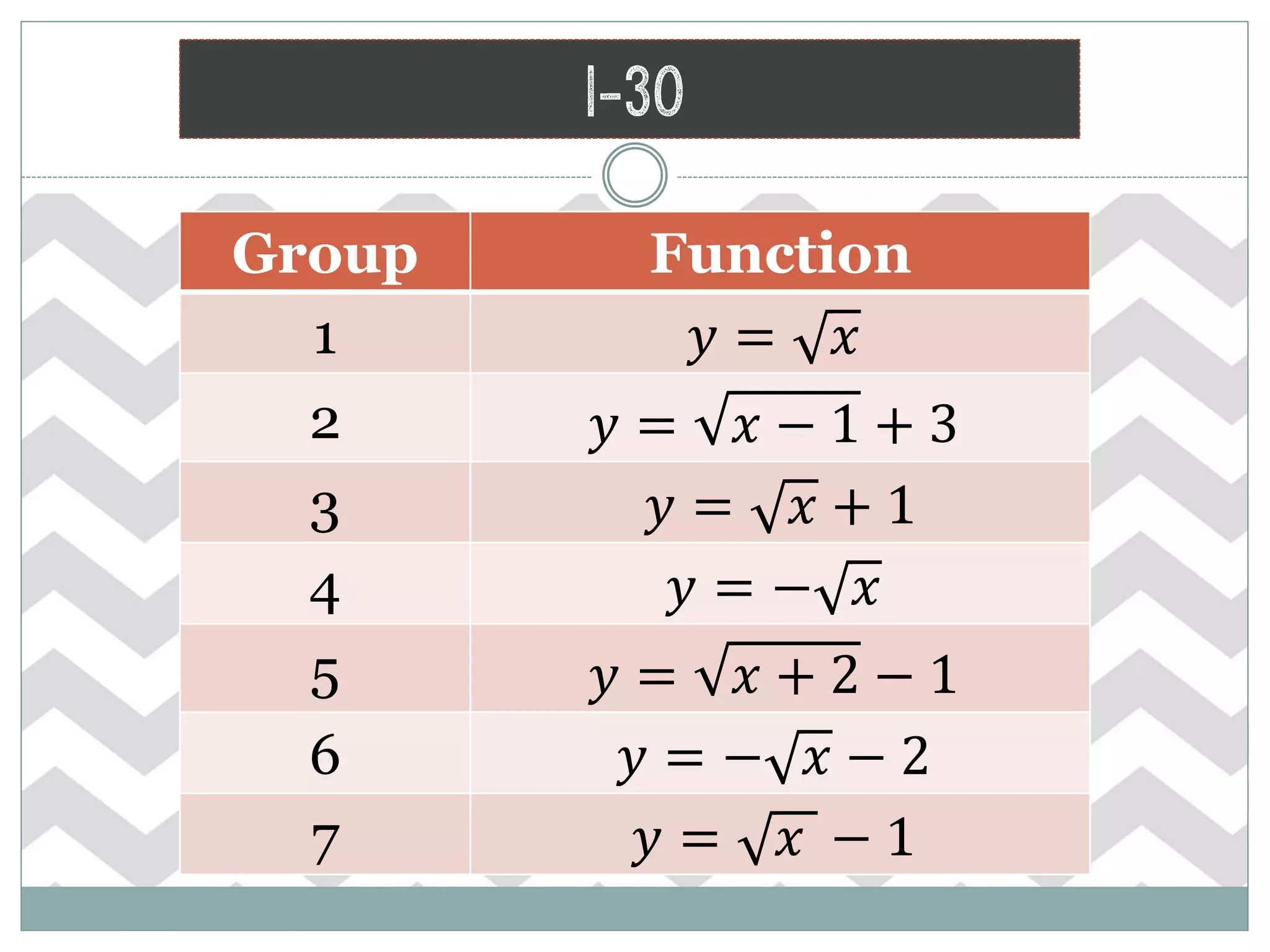
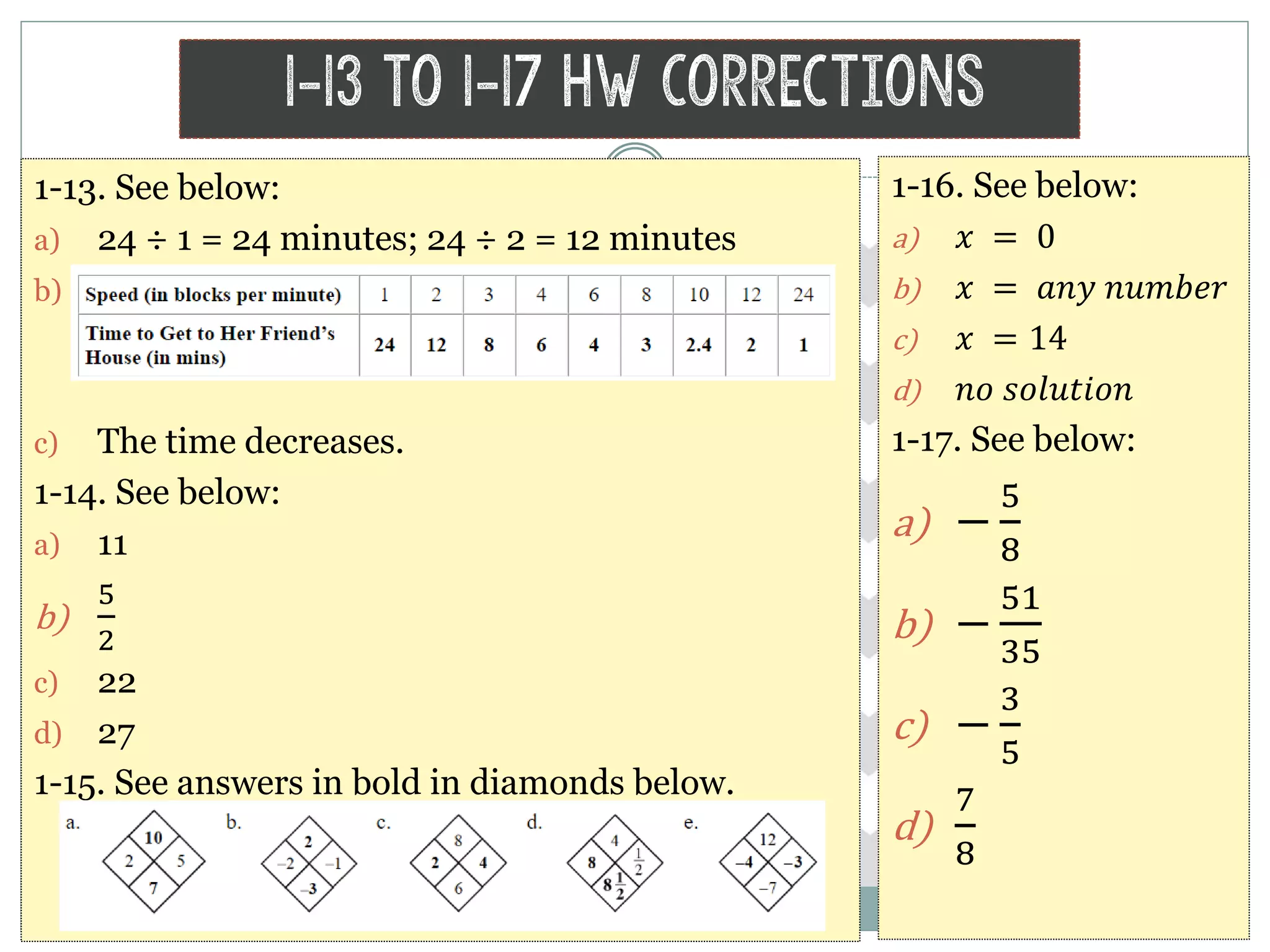
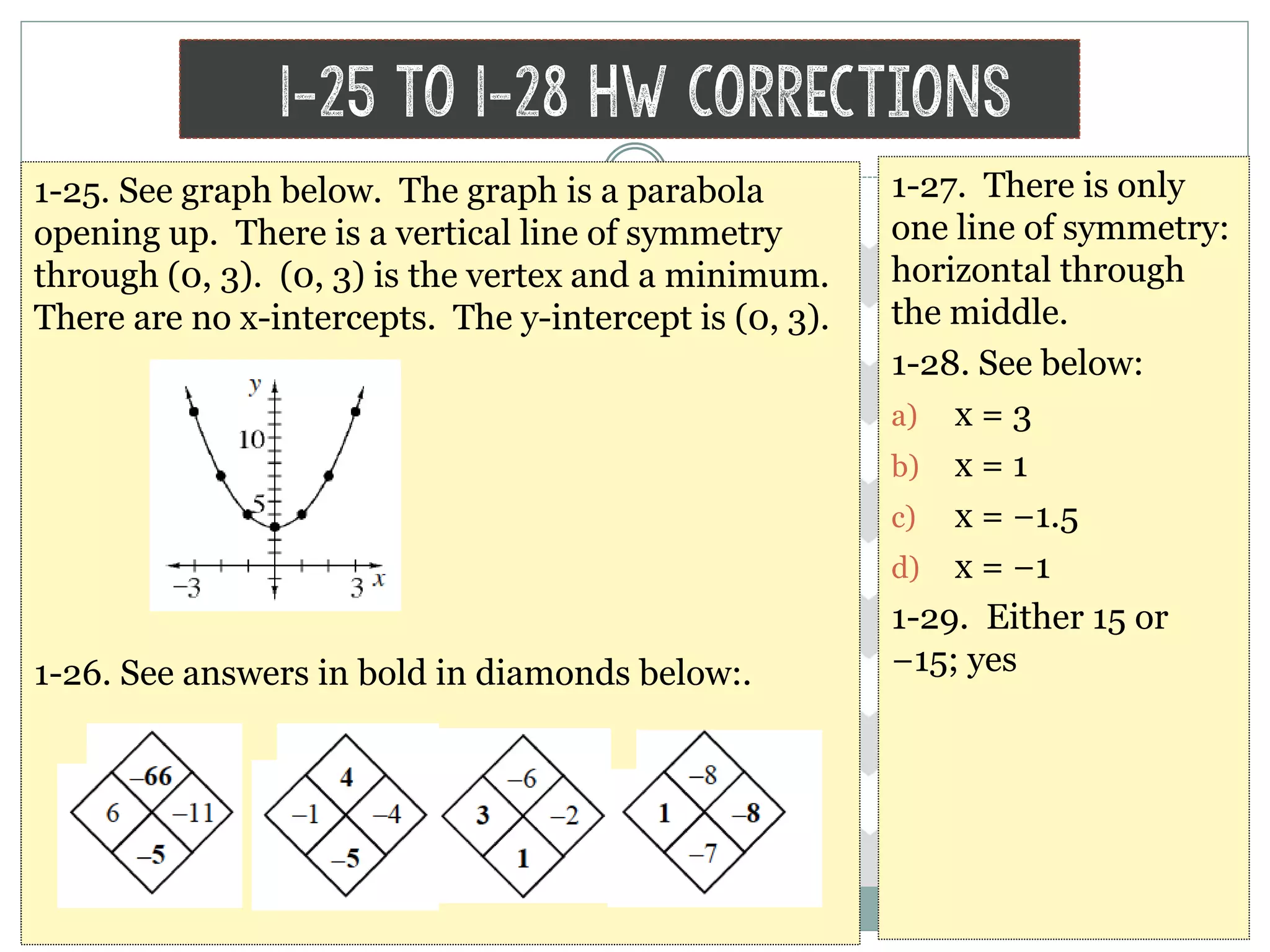
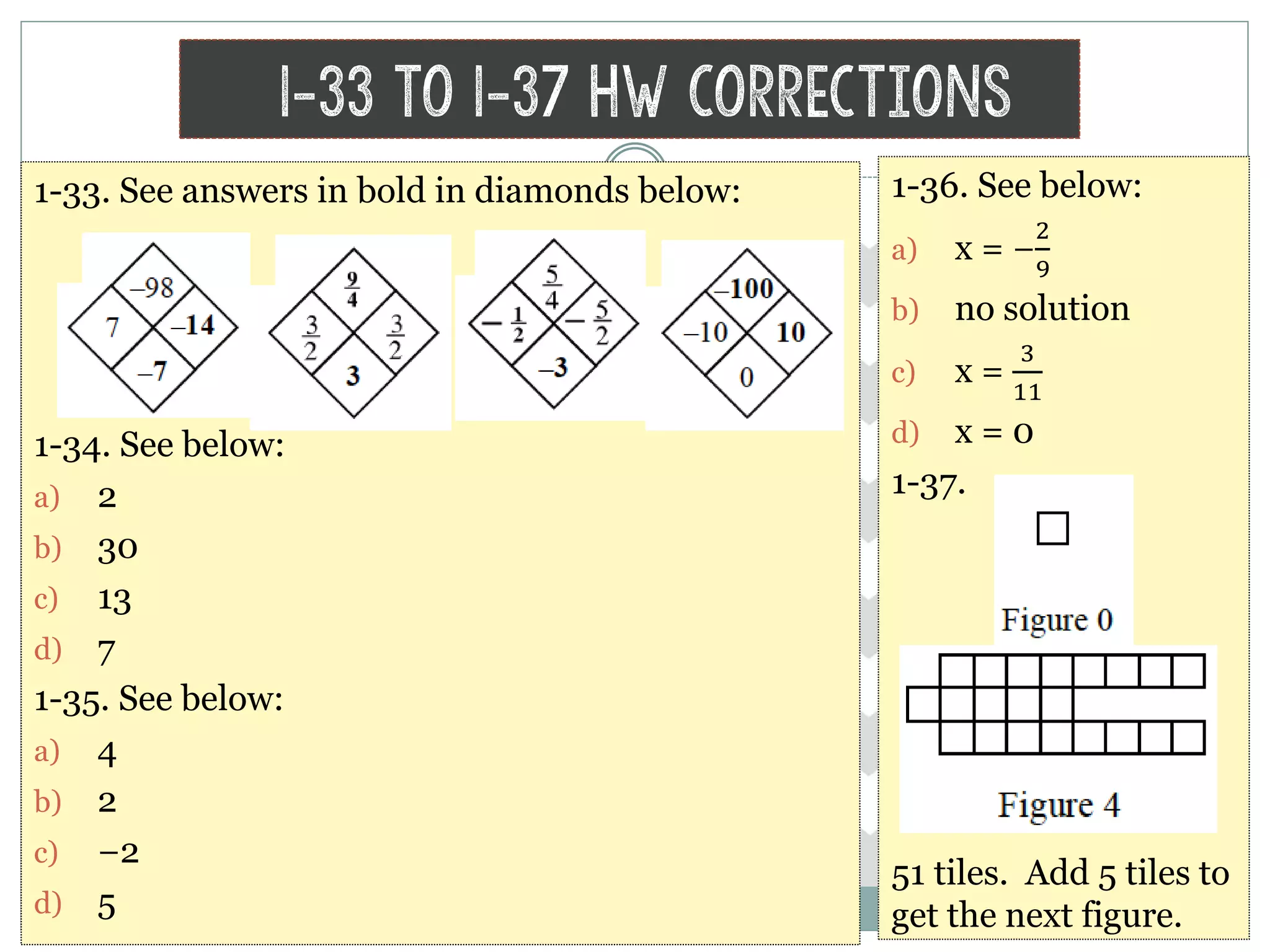
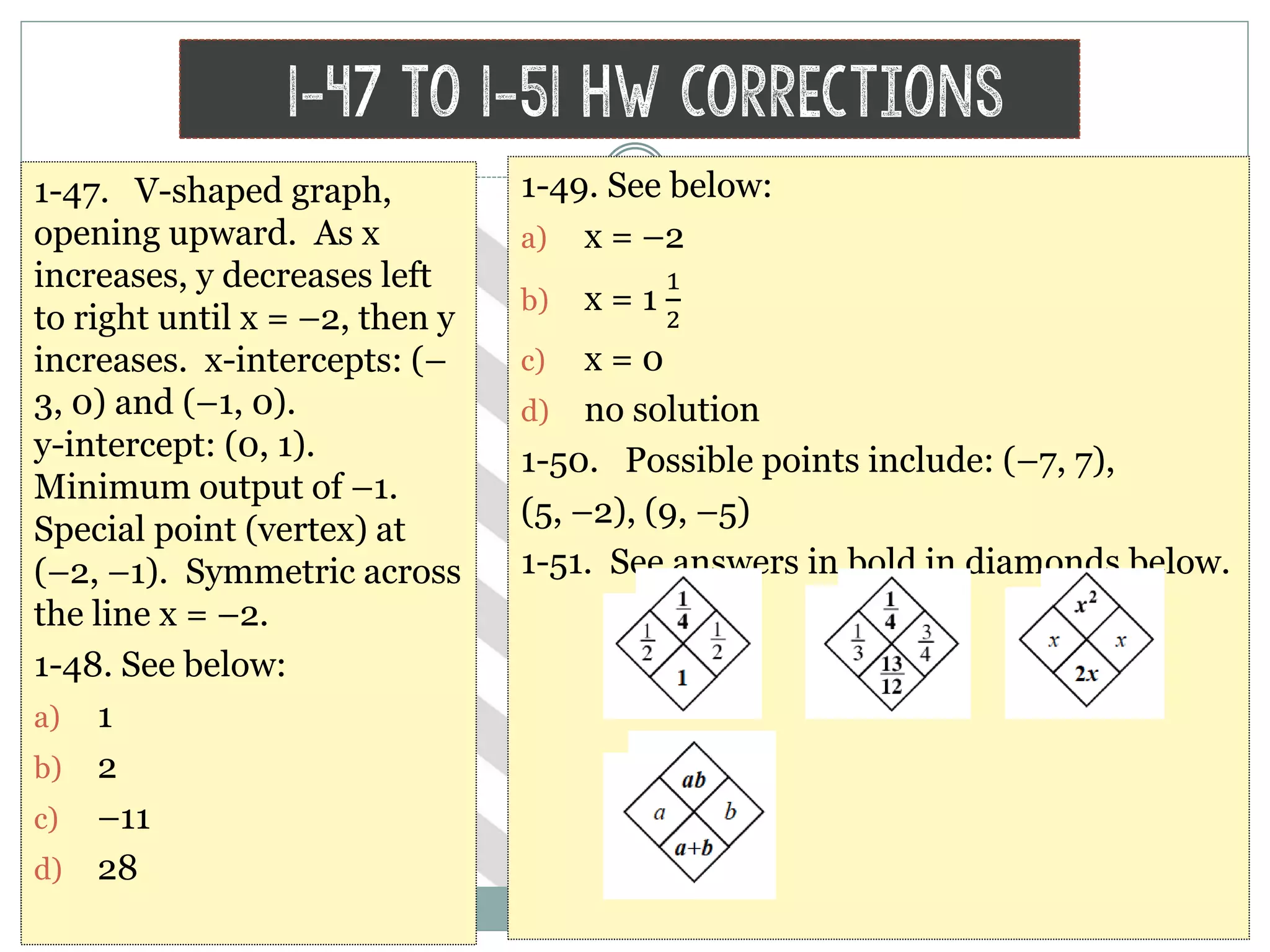
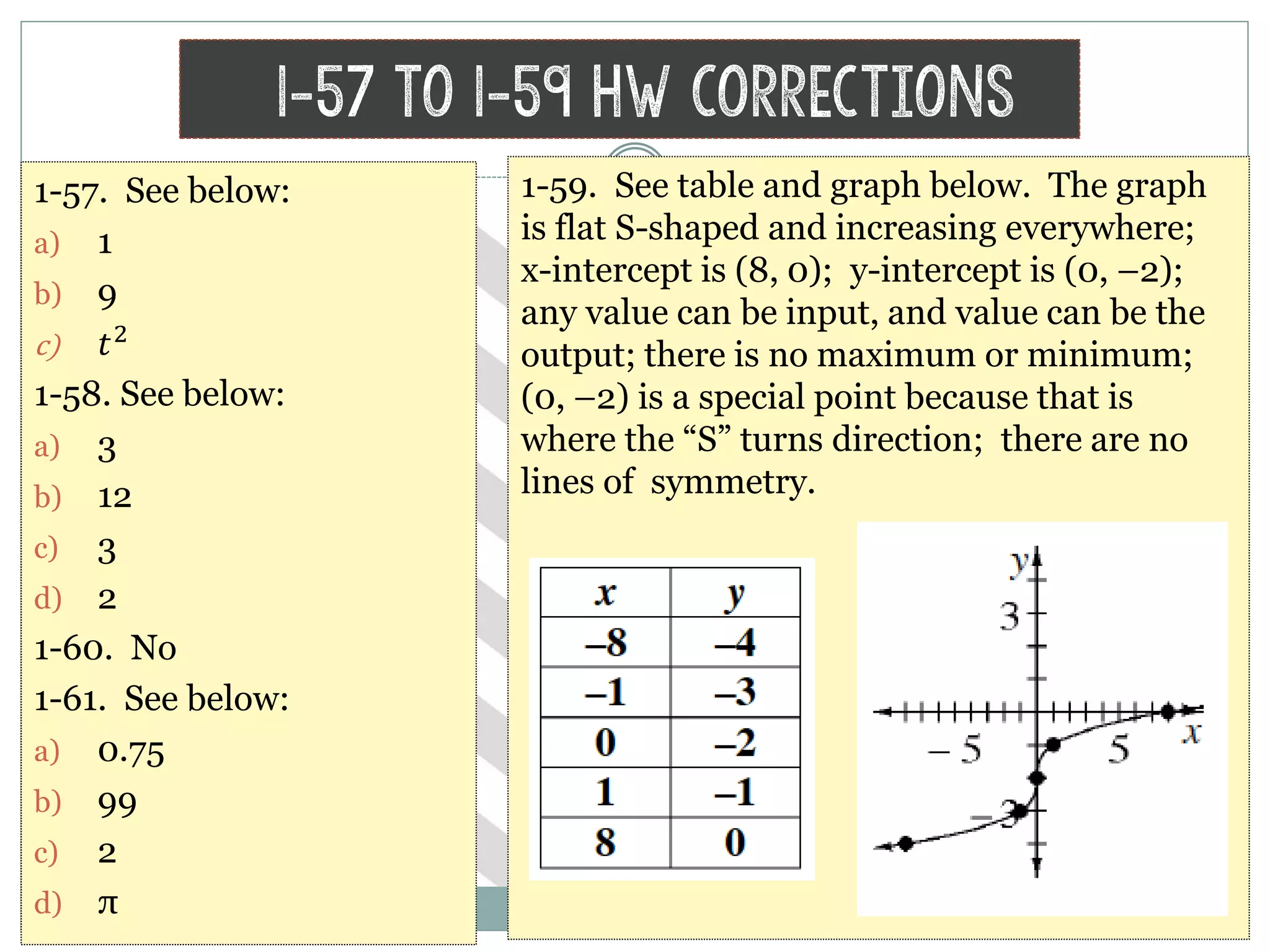
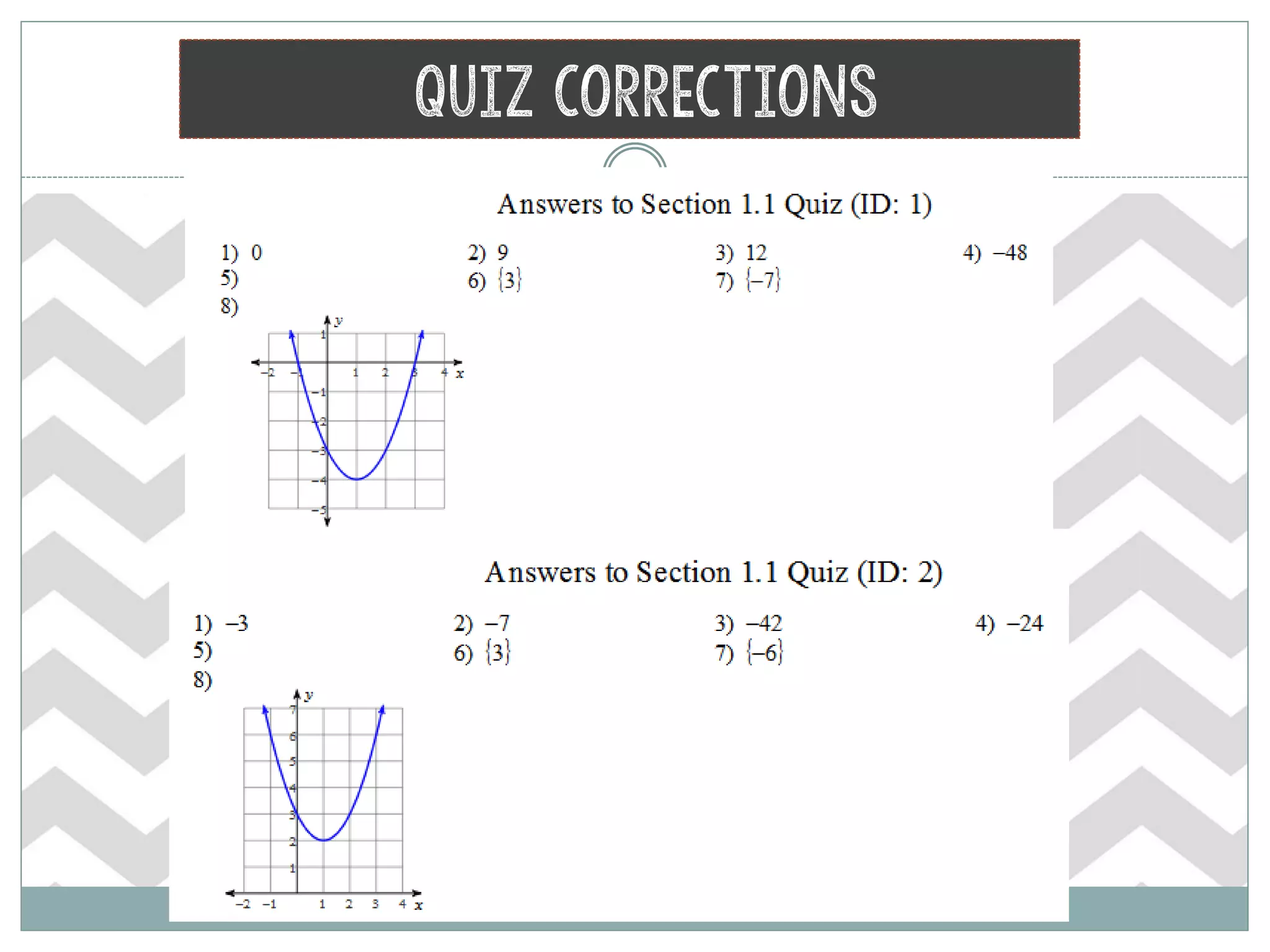
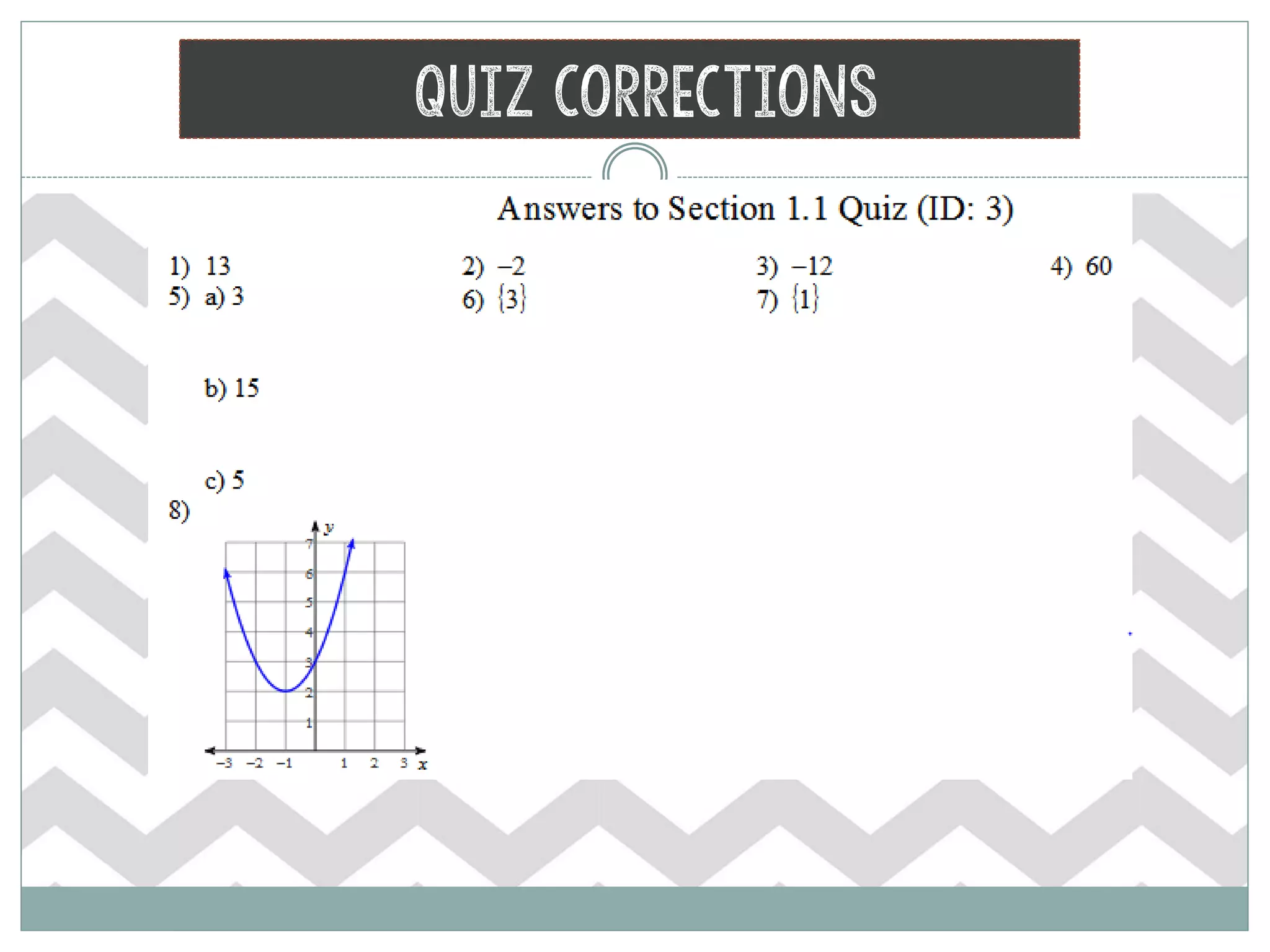
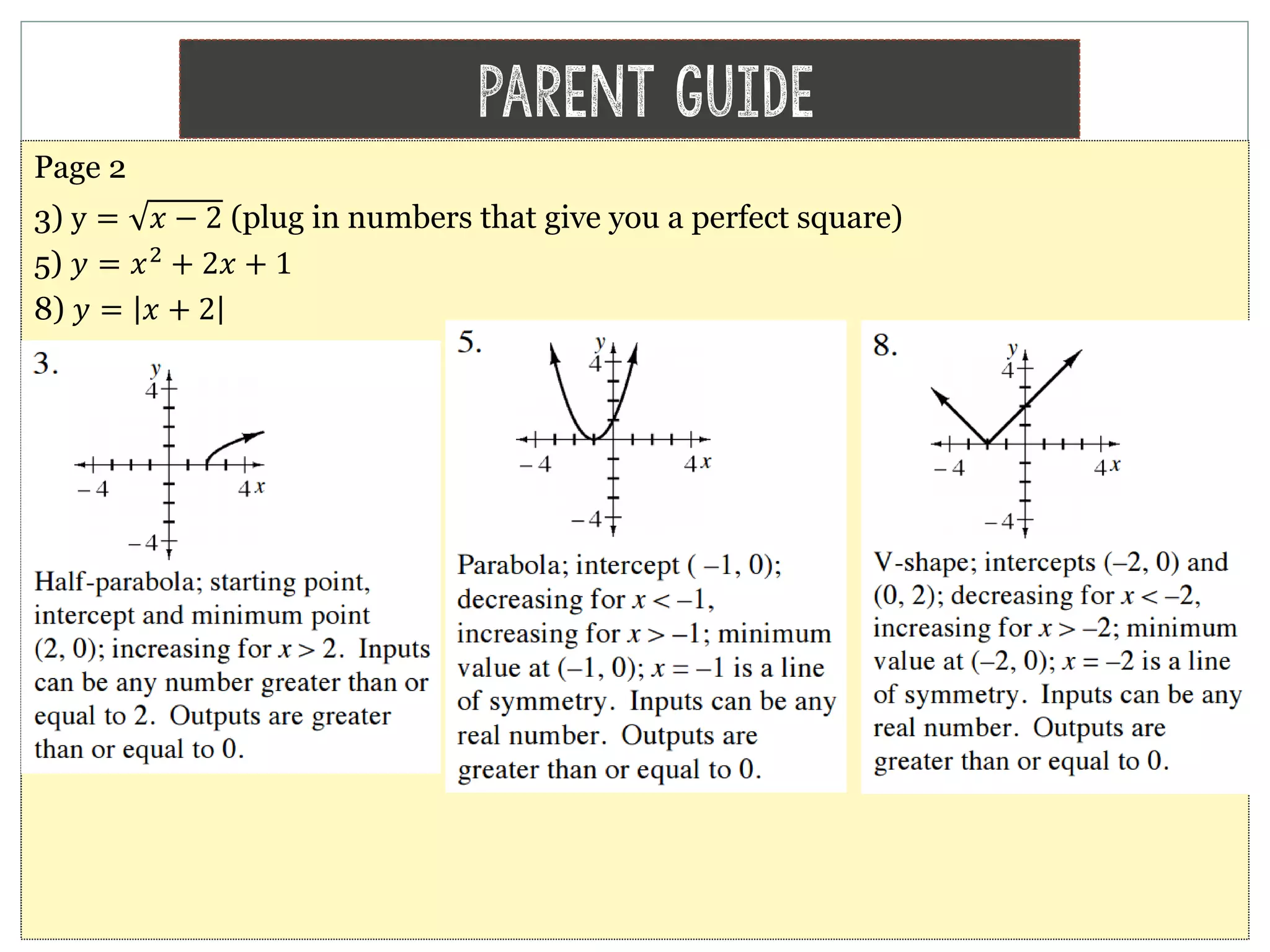
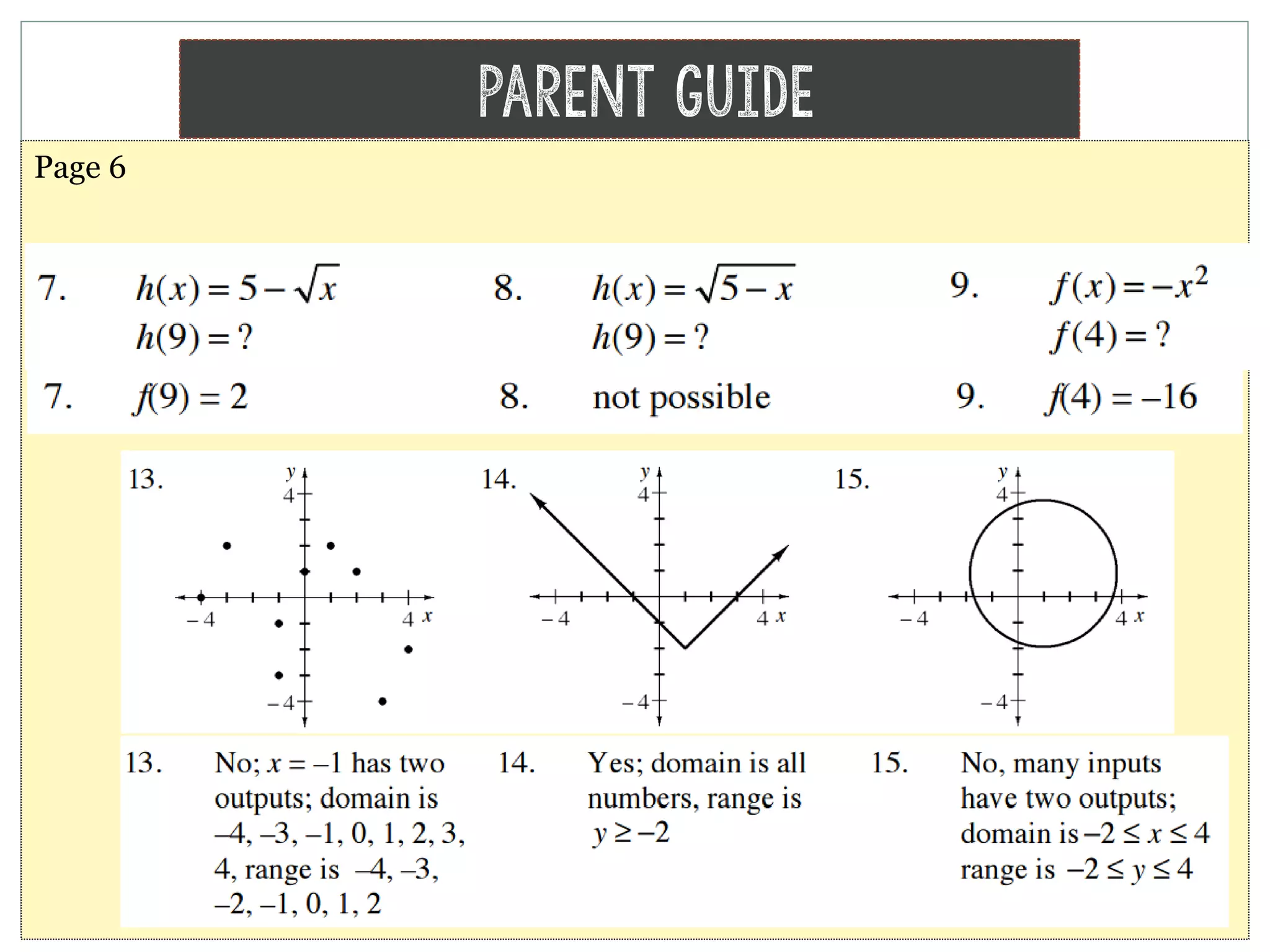
The document provides homework corrections and answers for various algebra problems from Chapter 1 on functions from Orcutt Academy High School's algebra 1 course, including corrections to homework problems, lab answers, and additional practice problems with worked out solutions shown.

1. O R C U T T A C A D E M Y H I G H S C H O O L
C O R E C O N N E C T I O N S A L G E B R A 1
Chapter 1 Functions

2. 1-4 to 1-8 HW Corrections
1-4. See below:
a) y = x2 − 6 and then y = 𝑥 − 5
b) Yes, reverse the order of the machines
(y = 𝑥 − 5 and then y = x2 − 6) and
use an input of x = 6.
1-5. See below:
a) 54
b) −7
3
5
c) 2
d) 2.93
1-6. See below:
a) (sketch figures)
b) It grows by two tiles each time.
c) 1
1-7. See below:
a) −59
b) 17
c) −72
d) 6
e) −24
f) −25
g) 25
h) −25
i) 7
1-8. See below:
a) 5
b) 3
c) 4

3. 1-9 Lab Answers

4. 1-18 to 1-22 HW Corrections
1-18. See below:
a) $18
b) 8.4 gallons
c) Typical response: The
line would get steeper.
1-19. See below:
a) x = −3
b) x = 5
c) x =
2
3
1-20. See below:
a) −8
b) −56
c) 3
d) 6
1-21. See answers in bold in diamonds below:
1-22. See below:
a) Function A = 84, Function B = no solution
b) He cannot get an output of 0 with Relation
A. He can get an output of 0 by putting a 4
in Function B.

5. 1-30
Group Function
1 𝑦 = 𝑥
2 𝑦 = 𝑥 − 1 + 3
3 𝑦 = 𝑥 + 1
4 𝑦 = − 𝑥
5 𝑦 = 𝑥 + 2 − 1
6 𝑦 = − 𝑥 − 2
7 𝑦 = 𝑥 − 1

6. Seed questions
1. Does this graph look like any other graphs you have seen? If so, how? If not,
describe the shape of the graph. Remember to give reasons for your
statements.
2. Do the y-values grow at a constant rate? If not, how do they grow? Do they
grow faster as x gets bigger? Remember to give reasons for your statements.
3. What happens to y as x gets bigger? What happens to y as x gets smaller?
Justify your conclusions.
4. Does this graph have any symmetry? If so, where? Remember to give
reasons for your statements.
5. Can all numbers go into this function? Why or why not? Can any number be
an output? Remember to justify your conclusions.
6. What special point(s) does your graph have? Is there a highest or a lowest
point? Remember to give reasons for your statements.
7. Is there a starting point or stopping point?
8. What is the x-intercept, if any? What is the y-intercept? What is the
maximum value of this function?
9. What is the minimum value?

7. 1-13 to 1-17 HW Corrections
1-13. See below:
a) 24 ÷ 1 = 24 minutes; 24 ÷ 2 = 12 minutes
b)
c) The time decreases.
1-14. See below:
a) 11
b)
5
2
c) 22
d) 27
1-15. See answers in bold in diamonds below.
1-16. See below:
a) 𝑥 = 0
b) 𝑥 = 𝑎𝑛𝑦 𝑛𝑢𝑚𝑏𝑒𝑟
c) 𝑥 = 14
d) 𝑛𝑜 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛
1-17. See below:
a) −
5
8
b) −
51
35
c) −
3
5
d)
7
8

8. 1-25 to 1-28 HW Corrections
1-25. See graph below. The graph is a parabola
opening up. There is a vertical line of symmetry
through (0, 3). (0, 3) is the vertex and a minimum.
There are no x-intercepts. The y-intercept is (0, 3).
1-26. See answers in bold in diamonds below:.
1-27. There is only
one line of symmetry:
horizontal through
the middle.
1-28. See below:
a) x = 3
b) x = 1
c) x = −1.5
d) x = −1
1-29. Either 15 or
−15; yes

9. Learning Log 1-32 graph investigation
1. What is the vertex? Does it have a highest (maximum) or lowest (minimum)
point?
2. Is it symmetric? What is the line of symmetry?
3. What are the x- and y- intercepts?
4. What is the shape of the graph? What does it look like?
5. Is it positive (increasing) or negative (decreasing)?
6. In what direction does the graph open?
7. What type of function? Square Root? Absolute Value? Linear? Quadratic?
Exponential?
8. Is it discrete or continuous?
9. Linear, what is the slope?

10. 1-33 to 1-37 HW Corrections
1-33. See answers in bold in diamonds below:
1-34. See below:
a) 2
b) 30
c) 13
d) 7
1-35. See below:
a) 4
b) 2
c) −2
d) 5
1-36. See below:
a) x = −
2
9
b) no solution
c) x =
3
11
d) x = 0
1-37.
51 tiles. Add 5 tiles to
get the next figure.

11. 1-47 to 1-51 HW Corrections
1-47. V-shaped graph,
opening upward. As x
increases, y decreases left
to right until x = –2, then y
increases. x-intercepts: (–
3, 0) and (–1, 0).
y-intercept: (0, 1).
Minimum output of –1.
Special point (vertex) at
(–2, –1). Symmetric across
the line x = –2.
1-48. See below:
a) 1
b) 2
c) –11
d) 28
1-49. See below:
a) x = –2
b) x = 1
1
2
c) x = 0
d) no solution
1-50. Possible points include: (–7, 7),
(5, –2), (9, –5)
1-51. See answers in bold in diamonds below.

12. 1-57 to 1-59 HW Corrections
1-57. See below:
a) 1
b) 9
c) 𝑡2
1-58. See below:
a) 3
b) 12
c) 3
d) 2
1-60. No
1-61. See below:
a) 0.75
b) 99
c) 2
d) π
1-59. See table and graph below. The graph
is flat S-shaped and increasing everywhere;
x-intercept is (8, 0); y-intercept is (0, –2);
any value can be input, and value can be the
output; there is no maximum or minimum;
(0, –2) is a special point because that is
where the “S” turns direction; there are no
lines of symmetry.

13. Quiz Corrections

14. Quiz Corrections

15. 1-66 to 1-70 HW Corrections
1-66. 1, 5, ≈ 8.54
1-67. See below:
a) x = –7
b) x = –1
c) x = 9
d) x = 34
1-68. See below:
a) 7
b) –20
c) 3
d) −5
1-69. See graph at right. It is a parabola
opening down. The vertex and maximum are
at (0, 3). There is a vertical line of symmetry
through (0, 3). The x-intercepts are
approximately (–1.75, 0) and (1.75, 0). There
is a vertical line of symmetry through (0, 3).
1-70. See below:
a) 8
b) 1
c) −2
d) no solution

16. 1-78 to 1-80 HW Corrections
1-78. See below:
a) Not a function because more than one y-value is
assigned for x between –1 and 1 inclusive
b) Appears to be a function
c) Not a function because there are two different y-
values for x = 7
d) Function
1-79. See below:
a) x-intercepts (–1, 0) and (1, 0),
y-intercepts (0, –1) and (0, 4)
b) x-intercept (19, 0),
y-intercept (0, –3)
c) x-intercepts (–2, 0) and (4, 0),
y-intercept (0, 10)
d) x-intercepts (–1, 0) and (1, 0),
y-intercept (0, –1)
1-80. See below:
a) 2
b) 53
1-81. See below:
a) yes
b) –6 ≤ x ≤ 6
c) –4 ≤ y ≤ 4
1-82. See below:
a) x = –8
b) x = 144
c) x = 3 or x = −5

17. Parent Guide
Page 2
3) y = 𝑥 − 2 (plug in numbers that give you a perfect square)
5) 𝑦 = 𝑥2
+ 2𝑥 + 1
8) 𝑦 = 𝑥 + 2

18. Parent Guide
Page 6