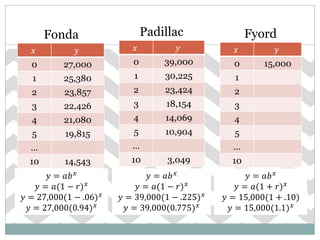
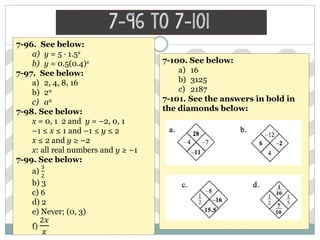
The document discusses depreciation rates for three cars: a 2010 Fonda Concord EX depreciating at 6% per year, a 2010 Padillac Escalate depreciating at 22.5% per year, and a 1967 Fyord Rustang appreciating at 10% per year. It tasks the reader with generating representations of the value of each car over time and determining which car Jeralyn should buy based on value retention from 2010 to 2012.

1. 7.1.1 Investigating 𝑦 = 𝑎𝑏 𝑥
𝑦 = 𝑏 𝑥
𝑃𝑜𝑠𝑡𝑒𝑟
𝑦 =
1
4
𝑥
𝑦 =
1
2
𝑥
𝑦 = 2 𝑥
𝑦 = 3 𝑥
𝑦 = 4 𝑥
Include Table, Graph, and Description!!!
Read Problem 7-4!

2. 7-7. See below:
a. If s is the price of a can of soup and b is the cost of a loaf of bread, then
Khalil’s purchase can be represented by 4s + 3b = $11.67 and Ronda’s by
8s + b = $12.89
b. soup = $1.35, bread = $2.09
7-8. Sometimes true; true only when x = 0
7-9. See below:
a. It can be geometric, because if each term is multiplied by , the next term
is generated.
b.
c. No, because the sequence approaches zero, and half of a positive number is
still positive.
7-10. See below:
a. 90cm
b. 37.97cm
c. t(n) = 160(0.75)n
7-7 to 7-19

3. 7-11. See below:
a. y = 5.372 – 1.581x
b. Yes. There is random scatter in the residual plot with no apparent pattern.
c. r = –0.952 and R2
= 90.7%. 90.7% of the variability in the length of a cold
can be explained by a linear relationship with the amount of time taking
supplements.
d. A residual plot with random scatter confirms the relationship is linear. It is
negative with a slope of –1.581, so an increase in one month of supplements
is expected to decrease the length of a cold by 1.581 days. The association is
strong: 90.7% of the variability in the length of a cold can be explained by a
linear relationship with the time taking supplements. There are no apparent
outliers.
7-12. See below:
a. 9x4
y2
z8
b.
c. 6m2
+ 11m – 7
d. x2
– 6x + 9
7-7 to 7-19

4. 7-13. ; 2.7 pounds
7-14. See below:
7-15. See below:
a. a1 = 108, an+1 = an +12
b. a1 = , an+1 = 2an
c. t(n) = 3780 – 39n
d. t(n) = 585(0.2)n
7-16. See below:
a. 1.25
b. 0.82
c. 1.39
d. 0.06
7-7 to 7-19

5. 7-17. See below:
a. No, by observation a curved regression line may be better. See
graph below.
b. Exponential growth. The growth is similar to the flu outbreak in Chapter 1
(Lesson 1.1.2).
c. m = 8.187 · 1.338d
, where m is the percentage of mold, and d is the number
of days. Hannah predicted the mold covered 20% of a sandwich on
Wednesday. Hannah measured to the nearest percent.
7-18. See below:
a. 94 years
b. From 1966 to 1999, 429 marbles were added, which means there were 13
marbles added per year.
c. 17
t(n) = 17 + 13n
In the year 2058, when the marble collection is 153 years old, it will contain more
than 2000 marbles.
7-19. See answers in bold in the diamonds below:

6. 7-24. See below:
See table below. y = 1.2(3.3)x
x y
0 1.2
1 3.96
2 13.068
3 43.1244
4 ≈ 142.31
See table below. y = 5 · 6x
x y
0 5
1 30
2 180
3 1080
4 6480
7-25.
Answers vary but should include a table, a
graph, and a situation.
7-3 to 7-40

7. 7-26. They are all parabolas, with
y = 2x2 rising most rapidly and
𝑦 =
1
2
𝑥2
most slowly. See solution
graph at right.
7-27. 9 weeks
7-28. See below:
a) arithmetic, t(n) = 3n – 2
b) neither
c) geometric, r = 2
d) arithmetic, t(n) = 7n – 2
e) arithmetic, t(n) = n + (x – 1)
f) geometric, r = 4
7-29. There is a weak negative
linear association: as dietary fiber
is increased, blood cholesterol
drops. 20.25% of the variability in
blood cholesterol can be explained
by a linear association with dietary
fiber.
7-26 to 7-29

8. 7-35 to 7-40
7-35. Simple interest at 20%,
let x = years, y = amount in the
account, y = 500 + 100x
7-36. See below:
a) y = 15 · 5x
b) y = 151(0.8)x
7-37. See below:
a) 8%, 1.08
b) cost = 150(1.08)8 = $277.64
c) $55.15 (An answer of $50.41
means a multiplier of 0.92
was used.)
7-38. See below:
a) y = 125000(1.0625)t
b) $504,052.30
7-39. See below:
a) Sample solution below.
The y-intercept and slope
could vary—the slope might
even be negative—but the
x-coordinates and the
position of the points
relative to each other are
precise.
The model made
predictions that were closer
to the actual values for
taller swimmers.
7-40. See below:
a) (4, –1)
b) (–1, –2)
c) Part (b)
d) Part (a).

9. Holt p. 752 #29-33
Holt p. 752 #29-33
29. 𝑦 = 58,000(1.001) 𝑡
, 58,174,174
30. 𝑦 = 32,000(1.07) 𝑡
, $44,881.66
31. 𝑦 = 8,200(.98) 𝑡
, $7,118.63
32. 𝑦 = 25,000(.85) 𝑡
, $9,428.74
33. 𝑦 = 970(1.012) 𝑡
, 1030

10. 7-48 to 7-52
7-48. See below:
0.40
$32, $2.05
V(t) = 80(0.4)t
According to this model, it never
will; but in reality, a DVD would
have no value if it breaks or if there
is no longer a mechanism to play it.
See graph below.
7-49. See below:
Let y = youngest child, y + (y + 5) +
2y = 57; The children are 13, 18 and
26 years
Let x = months, y = insects, y = 2x +
105, y = 175 – 3x; 14 months
Let x = amount paid, ; $4.80
Let a = # adult tickets, s = # student
tickets, 3s + 5a = 1770,
s = a + 30;
210 adult and 240 student
7-50. See below:
x2 – 6x + 9
4m2 + 4m + 1
x3 – 2x2 – 3x
2y3 – y2 + 14y – 7
7-52. See answers in bold in the
diamond below:

11. CW 7-59
7-59
a. y = 5(1.4)x
b. y = 40(
1
3
)x
c. y = 7(2)x
d. y = 18(1)x
e. y = 3(5)x
f. y = –8(2)x
Tape in Notebook!

12. Homework 7-53 to 7-58
7-53. See below:
a. –3 b.
1
2
7-54. 0.8%; y = 500(1.008)m
7-55. See below:
(–8, 2)
(
5
3
, –1)
7-56. 𝑦 =
9
4
𝑥 + 9
7-57. See below:
y = –132 + 2.29x
The U-shaped residual plot indicates a non-linear model may be better.
The residual plot shows no apparent pattern, so the power model is
appropriate.
y = 0.118x1.467
7-58. See below:
Sometimes true (when x = 0)
Always true
Sometimes true (for all values of x and for all y except y = 0)
Never true

13. Homework 7-61 to 7-66
7-61. See graph below:
7-62. y = 4(1.75)x
7-63. See below:
y = 500(1.08)x
$1712.97
x ≥ 0, y ≥ 500
7-64. Both have the same shape
as y = x2, but one is shifted up 3 units
and the other is shifted left 3 units. See
graphs below.
7-65. See below:
a. –10 b.
1
2
c. –5 d. 3
7-66. See below:
a = 0
m =
16
17
x = 10
x = 9, –3

14. Classwork 7-67 to 7-71
7-67. Sample answers:
a. value of a new car
b. value of an antique
c. population of a country
7-68.
No because y = 0 is an asymptote
Yes because eventually the value of the
function will fall below 1 and there
cannot be a fraction of a fish.
7-69. See below:
y = 7000(1.10)x
y = 7000(1.10)9 = $16,505.63
y = 7000(1.10)–10 = $2698.80
The model has been extrapolated far
from the known data.
The expected amount is $8470. The
residual in 2012 was –$226
7-70. See below:
a. b.
c.
7-71. Answers vary.
y = 100(0.94)x; about 4.005 grams
y = 45(1.30)x; 167 members
y = 160(0.89)x; about six weeks
y = 285(1.015)x; $340.75

15. Homework 7-73 to 7-78
7-73. See below:
a. y = 281.4(1.02)5,
310.7 million people
b. 343.0 million people
c. –34 million people.
Population growth has slowed.
7-74.
a. a = 6, b = 2
b. a = 2, b = 4
7-75. See below:
a.
3𝑥3
𝑦5 b.
𝑚4
4𝑞4
7-76. See below:
a. 2, 6, 18, 54
b. c.
b. Domain is non-negative integers.
d. They have the same shape, but (b) is
discrete and (c) is continuous.
7-77. (–3, –6)
7-78. Weight is very strongly positively
associated with radius in a non-linear
manner with no apparent outliers. A
quadratic regression makes a good
model.

16. Holt p. 763 #1-10,12-14
1. 48, 96, 192
2. -16, 32, -64
3. -150, -75, -37.5
4. 4,374
5. 262.144 cm
6. 4.39 in.
11. 14 h
12. 𝑦 = 30,000(1.03) 𝑥
; $40,317.49
13.
𝑦 = 2,000(1.00375)12𝑥; $2,288.50
14. 𝑦 = 1,200(0.8) 𝑥
; $491.52
7 8
9 10

17. 7.2.2 More Curve Fitting
7-92. Mitchell was working on his algebra homework, when suddenly he had an
idea about finding linear equations. He was trying to find the equation of the
line that passes through the points (5, 15) and (3, 7). “Look!” he exclaimed. “We
know that the line can be written in the form y = mx + b, and we also know that
the points (5, 15) and(3, 7) have to make the equation true. So we can substitute
in these two points to create a system of equations. When we solve that, we’ll
know the values of m and b, and we’ll have our equation!”
a) What is Mitchell talking about? Use his method to find the equation of
the line through the points (5, 15) and (3, 7).
b) Will Mitchell's method work to find the equation of a line through any
two points? Justify your answer.

18. 7-93. Use Mitchell’s method from problem 7-92 to find the equation of the line
that passes through the points (2, 3) and (5, –6).
7-94. Can Mitchell’s method from problem 7-92 be used to find
the exponential function that passes through the points (2, 16) and (6, 256)?
Consider this as you answer the questions below.
What is the general form for an exponential function that has an asymptote
at y = 0?
Use the two points that you know to create a system of equations.
Solve both equations for a. Then use the Equal Values Method to solve your
system of equations for b. Find a, and write the equation that goes through
the two points.

19. 7-95. Find an exponential function that passes through each pair of points.
a) (−1, −2) and (3, −162)
b) (2, 1.75) and (−2, 28)

20. 7-102 FAST CARS Poster
7-102. FAST CARS
The moment you drive a new car off the dealer’s lot, the car is worth less than
what you paid for it. This phenomenon is called depreciation, which means you
will sell the car for less than the price that you paid for it. Some cars depreciate
more than others (that is, they depreciate at different rates), but most cars
depreciate over time. On the other hand, some older cars actually increase in
value. This is called appreciation. Let’s suppose that in 2012, Jeralyn had a
choice between buying a 2010 Fonda Concord EX for $27,000, which depreciates
at 6% per year; a 2010 Padillac Escalate for $39,000, which depreciates at 22.5%
per year; or a 1967 Fyord Rustang for $15,000 that is appreciating at 10% per
year.
Your Task: Investigate the value of each of the three cars over time.
Generate multiple representations of the value of each car over time.
For each of the new cars, determine how much value they lost (in dollars)
from the time they were new in 2010 until 2012.
Decide which car Jeralyn should buy and defend your choice in as many
ways as you can.
Refer to problem 7-103 for Further Guidance

21. 𝑥 𝑦
0 27,000
1 25,380
2 23,857
3 22,426
4 21,080
5 19,815
…
10 14,543
𝑥 𝑦
0 39,000
1 30,225
2 23,424
3 18,154
4 14,069
5 10,904
…
10 3,049
𝑥 𝑦
0 15,000
1
2
3
4
5
…
10
Fonda Padillac Fyord
𝑦 = 𝑎𝑏 𝑥
𝑦 = 𝑎(1 − 𝑟) 𝑥
𝑦 = 27,000(1 − .06) 𝑥
𝑦 = 27,000(0.94) 𝑥
𝑦 = 𝑎𝑏 𝑥
𝑦 = 𝑎(1 − 𝑟) 𝑥
𝑦 = 39,000(1 − .225) 𝑥
𝑦 = 39,000(0.775) 𝑥
𝑦 = 𝑎𝑏 𝑥
𝑦 = 𝑎(1 + 𝑟) 𝑥
𝑦 = 15,000(1 + .10)
𝑦 = 15,000(1.1) 𝑥

23. 7-87 to 7-91
7-87. See below:
a) y = 2 · 4x
b) y = 4(0.5)x
7-88. See below:
a) a = 3, b = 5
b) a = 2, b = 3
7-89. See below.
a) –4
b) 2
c) –2
d) 10
7-90. Possibilities: 8, 23, (163)1/4, (161/4)3, , etc.
7-91. Equation: y = 4x – 12; intercepts: (3, 0) and (0, –12)

24. 7-96 to 7-101
7-96. See below:
a) y = 5 · 1.5x
b) y = 0.5(0.4)x
7-97. See below:
a) 2, 4, 8, 16
b) 2n
c) an
7-98. See below:
x = 0, 1 2 and y = –2, 0, 1
–1 ≤ x ≤ 1 and –1 ≤ y ≤ 2
x ≤ 2 and y ≥ –2
x: all real numbers and y ≥ –1
7-99. See below:
a)
3
2
b) 3
c) 6
d) 2
e) Never; (0, 3)
f)
2𝑥
𝑥
7-100. See below:
a) 16
b) 3125
c) 2187
7-101. See the answers in bold in
the diamonds below:

25. Holt p. 425 #1-21
1.5
2.2
3.4
4.0
5.3
6.9
7.6
8.1
9.5
10.7
11.10
12.5
13.4
14.27
15.32
16.25
17.125
18.216
19.256
20.1
21.0