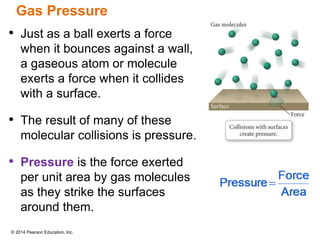
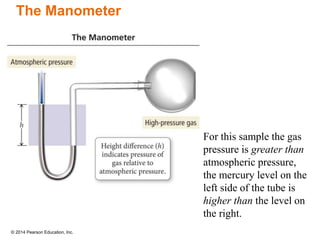
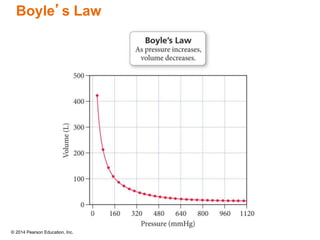
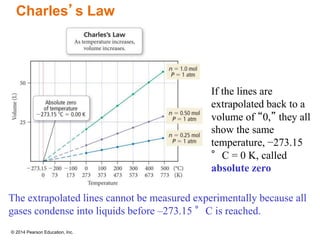
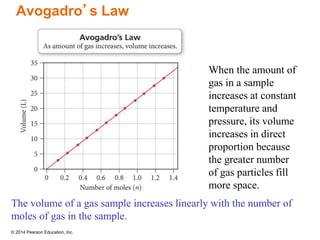
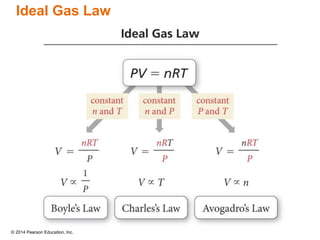
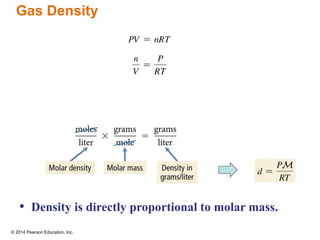
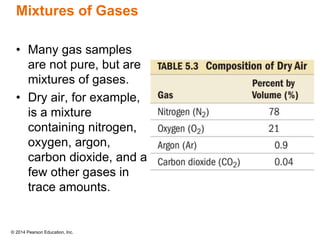
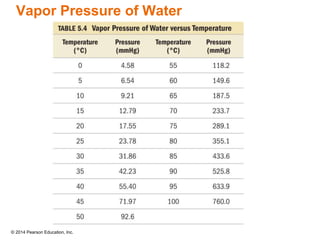
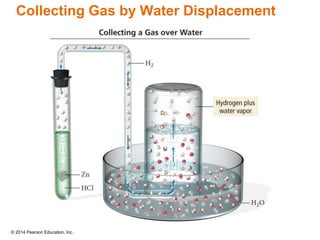
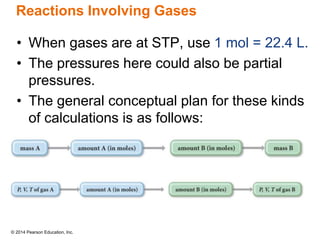
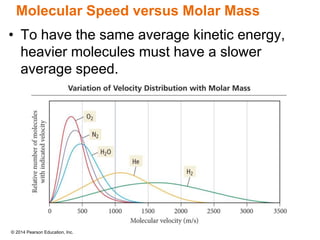
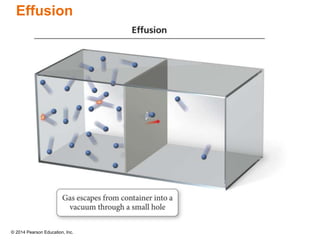
Gas particles move rapidly in straight lines, colliding elastically with each other and the container walls. The constant bombardment of particles on container surfaces results in gas pressure. Gas pressure depends on several factors, including the number of gas particles, volume of the container, and average particle speed. The ideal gas law combines relationships between pressure, volume, temperature, and amount of gas into a single equation. Gases behave independently in mixtures, and the total pressure equals the sum of the partial pressures of the individual gases.