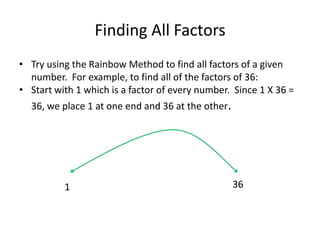
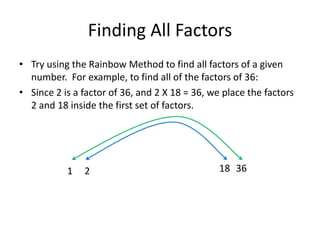
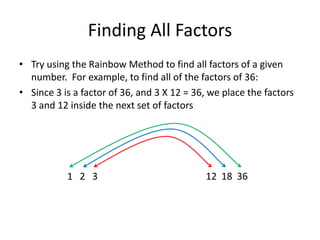
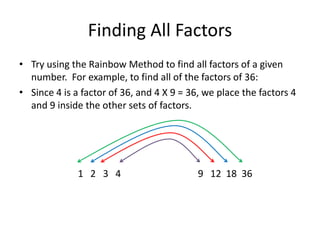
1) The document discusses factors, prime numbers, and composite numbers and how to use them to reduce fractions and find equivalent fractions. 2) It explains how to find all factors of a number using the rainbow method and defines prime and composite numbers. 3) It also covers prime factorization, using factor trees to break numbers down into their prime factors, and how to reduce fractions to lowest terms.

1. Fractions and FactorsIn order to work with fractions efficiently, it is important to understand some concepts about factors, prime numbers and composite numbersWe will use these concepts to develop equivalent fractions when we need to reduce a fraction to lowest terms or change fractions to one with a common denominator.

2. FactorsFactors are the numbers that are multiplied together to get a product.We can write 12 as the product of two factors in any of the following ways: 3 • 4 = 12 2 • 6 = 12 1 • 12 = 12If asked for all of the factors of 12, the answer would be:1, 2, 3, 4, 6, and 12

3. Finding All FactorsTry using the Rainbow Method to find all factors of a given number. For example, to find all of the factors of 36:Start with 1 which is a factor of every number. Since 1 X 36 = 36, we place 1 at one end and 36 at the other. 361

4. Finding All FactorsTry using the Rainbow Method to find all factors of a given number. For example, to find all of the factors of 36:Since 2 is a factor of 36, and 2 X 18 = 36, we place the factors 2 and 18 inside the first set of factors. 361 2

5. Finding All FactorsTry using the Rainbow Method to find all factors of a given number. For example, to find all of the factors of 36:Since 3 is a factor of 36, and 3 X 12 = 36, we place the factors 3 and 12 inside the next set of factors1 2 312 18 36

6. Finding All FactorsTry using the Rainbow Method to find all factors of a given number. For example, to find all of the factors of 36:Since 4 is a factor of 36, and 4 X 9 = 36, we place the factors 4 and 9 inside the other sets of factors.1 2 3 4 9 12 18 36

7. Finding All FactorsTry using the Rainbow Method to find all factors of a given number. For example, to find all of the factors of 36:Now we try 5. But that is not a factor of 36, so we go on to 6. 6 X 6 = 36, so we include the factor 6 in our rainbow. We have already captured all of the factors greater than 6, so we are done.1 2 3 4 69 12 18 36Solution: All of the factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36

8. Prime and Composite NumbersA Prime number can only be divided by 1 and itself. The first 10 prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 A Composite number is composed of more than one prime factor and can be divided by other factors, as well as 1 and itself. The first 10 composite numbers are: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18 NOTE: The number 1is considered neitherprime nor composite.

9. Prime FactorizationIt is sometimes necessary to be able to break a number down into its prime factors. This process is called Prime Factorization. We can use a factor tree to determine the prime factorization of a number.To determine the prime factorization of 12, we first choose any set of factors for 12, such as 3 X 4 12 / \ 4 / \ 2 23 is already a prime number, but 4 is not,So we break it down into its factorsSolution: the prime factorization of 12 is 3 •2 • 2

10. Prime FactorizationAnother example: Let’s define 120 as a product of its prime factors (find the prime factorization of 120) First, we find any two factors of 120.

11. Then, if the factor is prime, we circle it.

12. If not prime, we factor again and circle the primesContinue until we only have primes.Solution: the prime factorization of 120is 2 • 2 •2 •3 • 5

13. Reduce a Fraction to Lowest TermsWrite fraction in lowest terms using the Prime Factoring method.First, write the numerator and denominatoras the product of their primes.Divide out any common factors. Since 2 and 3 have no more common factorsThe fraction is in lowest terms.

14. Finding an Equivalent Fraction3Let’s say we need to rewrite — with a denominator of 15.5Remember that if we multiply numeratorand denominator by the same number, we get an equivalent fraction.Since 5 •3 = 15, we need to multiply thenumerator by 3 as well.= 1 -- So when we multiply both numerator and denominator by 3 we are multiplying the original fraction by 1.