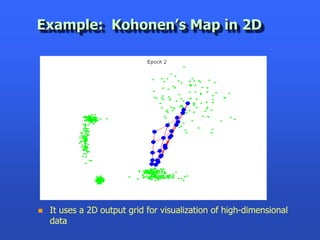
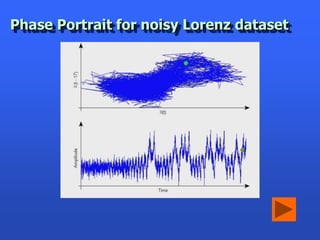
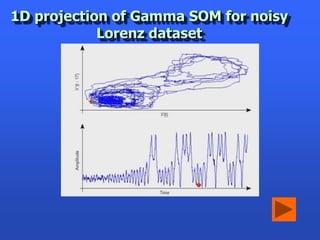
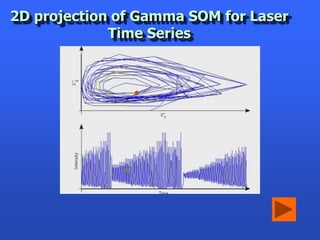
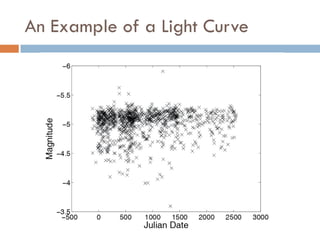
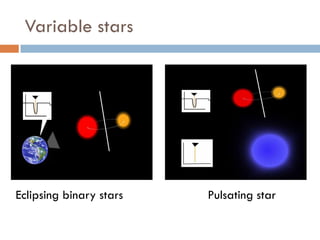
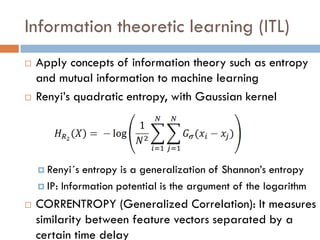
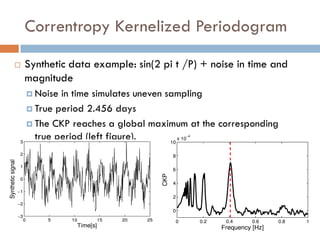
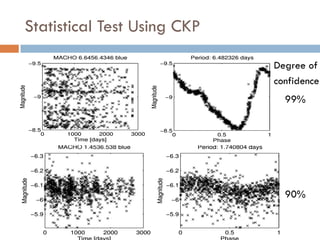
This document summarizes a presentation on analyzing astronomical time series data using information theoretic learning approaches. It discusses challenges with irregularly sampled and noisy light curve data from astronomical surveys. It proposes using correntropy, a generalized correlation measure, within a periodic kernel to create a Correntropy Kernelized Periodogram (CKP) for discriminating periodic vs non-periodic light curves and estimating periods of periodic curves. It applies this approach to real survey data from MACHO and EROS, achieving high classification accuracy and ability to process billions of light curves efficiently using GPU clusters.

1. Pablo A. Estévez, DIE, Universidad de Chile
Joint work with
Pavlos Protopapas, University of Harvard
Pablo Zegers, Universidad de los Andes, Chile
Pablo Huijse, PhD Student, Universidad de Chile
Jose C. Principe, University of Florida, Gainesville
ASTRONOMICAL TIME SERIES
ANALYSIS USING INFORMATION
THEORETIC LEARNING
Workshop on CI Challenges, September 2012

2. Astronomical Time Series: Light Curves
 Light Curve: Stellar brightness (magnitude or flux)
versus time.
 Variable stars: stars whose luminosity varies over
time (3% of the stars in the universe are variables,
and 1% are periodic variable stars)
 Light Curve Analysis: Useful for period detection,
event detection, stellar classification, extra solar
planet discovery, measure distance to earth, etc.

3. An Example of a Light Curve

4. Challenges
 Light curves are unevenly spaced or irregularly
sampled, with gaps of different sizes. This is due to:
 Time constraints on the observation time
 Day-night cycle, weather conditions
 Equipment operability
 Light curves are noisy due to photometric errors,
atmospheric and sky background
 Astronomical surveys generate tens of millions of
light curves. Light curve generation rate will continue
growing during the next years.

5. Variable stars
Eclipsing binary stars Pulsating star

6. Problem Statement
 Discriminate periodic versus non-periodic light
curves in astronomical survey databases
 Estimate the underlying period of periodic light
curves.
 Goal: To develop an automated method for
periodic detection and estimation based on
information theoretic learning.

7. Information theoretic learning (ITL)
 Apply concepts of information theory such as entropy
and mutual information to machine learning
 Renyi’s quadratic entropy, with Gaussian kernel
 Renyi´s entropy is a generalization of Shannon’s entropy
 IP: Information potential is the argument of the logarithm
 CORRENTROPY (Generalized Correlation): It measures
similarity between feature vectors separated by a
certain time delay

8. Proposed discrimination metric
 It combines correntropy (generalized correlation)
with a periodic kernel
 The periodic kernel measures similarity among
samples separated by a given period
 The new metric provides a periodogram, whose
peaks are associated with the fundamental
frequencies present in the data
 It is computed directly from the available samples
 Correntropy Kernelized Periodogram (CKP)

9. Correntropy Kernelized Periodogram
 Synthetic data example: sin(2 pi t /P) + noise in time and
magnitude
 Noise in time simulates uneven sampling
 True period 2.456 days
 The CKP reaches a global maximum at the corresponding
true period (left figure).

10. Statistical Test Using CKP
Degree of
confidence
99%
90%

11. Receiver Operator Characteristic
ROC curves for CKP, and alternative methods: LS-periodogram and AoV-
periodogram. Dataset: 750 periodic light curves and 1500 aperiodic light
curves from the MACHO survey. Due to the natural classs imbalance, very low
false positive rates are required (0.1%).

12. EROS Survey
 Survey of the Magellanic Clouds and the Galactic bulge
 Data taken from ESO Observatory, in La Silla, Chile
 EROS main goal: search for the dark matter of the
Galactic halo
 EROS survey is a goldmine for stellar variability studies:
Cepheids, RR-Lyrae, Eclipsing Binaries, and Supernovas.
 Each EROS field has ~17,300 light curves.
 There are 88x32 fields of the Large Magellanic Cloud
(LMC), i.e.
48.744.522 light curves =>48.7M light curves

13. Computational Time Requirements
for EROS Survey
 Computational time measured using NVIDIA Tesla C2070
GPU (448 cores)
 Sweeping 20000 trial periods with CKP, the total time
per light curve (~650 samples): 1.5 [s]
 For 48.7M light curves: ~845 days!
 Evaluating 600 precomputed trial periods (by using
correntropy and other methods) and optimizing the code:
0.2 [s] per light curve
 For 48.7M million light curves: ~113 days!

14. NCSA Dell/NVIDIA Cluster: FORGE
 National Center for Supercomputing Applications (NCSA)
at the University of Illinois at Urbana-Champaign
 We are using a queue with 12 machines each having 8
cores with Tesla C2070 GPUs => 96 GPUs
 Computing eight EROS fields using a machine with 8 cores
takes 1 hour
 So far we have processed 1.2M light curves in 40 mins
 At this rate for computing 48.7M light curves: ~30 hours!
 FORGE has 44 machines with 288 GPUs in total. Using
the whole cluster we might process 1 BILLION light curves
in 10 days

15. Conclusions & Future Work
 A framework for light curve analysis based on ITL
and kernel methods has been introduced.
 CKP allows discriminating between periodic and
non-periodic light curves with high accuracy and
low number of false positives.
 Required: Efficient computation of ITL based
methods
 Challenge: Applying our methods to large
untested astronomical databases.

16. ALMA Site in Northern Chile

17. THE END
 P.Huijse, P. Estevez, P. Zegers, P. Protopapas, J.
Principe, “Period Estimation in Astronomical Time
Series using Slotted Correntropy”, IEEE Signal
Processing Letters, Vol. 18, n°6, pp. 371-374,
2011.
 P.Huijse, P. Estevez, P. Protopapas, P. Zegers, J.
Principe, “An Information Theoretic Algorithm for
Finding Periodicities in Stellar Light Curves”, IEEE
Transactions on Signal Processing, Vol. 60, n°10, pp.
5135-5145, 2012.

18. Computational Intelligence Applied to
Time Series Analysis
Pablo A. Estévez
Department of Electrical Engineering
University of Chile
University of Cyprus, Cyprus
September 14, 2012

19. Outline
First Topic
 Introduction to Self-Organizing Maps (SOM)
 SOMs for temporal sequence processing
 Short-term Gamma Memories
 Experimental Results
 Conclusions
Second Topic
 Analysis of Astronomical Time Series
 Information Theoretic Learning Approach

20. Kohonen’s Map
 Self-Organizing Feature Map (SOM)
 Unsupervised Neural Networks
 Vector Quantization of Feature Space
 Topological Ordered Mapping
 Main Applications:
 Dimensionality reduction
 Visualization of high-dimensional data in 2D or 3D maps
 Clustering
 Knowledge discovery in Databases

21. Topological Ordered Map
 SOM defines a fixed grid in output space
 Each node in the output grid is associated with
a prototype (codebook) vector in input space
 Neighborhood is measured in the output space
 This neighborhood is used for updating
codebook vectors in input space

22. Example: Kohonen’s Map in 2D
 It uses a 2D output grid for visualization of high-dimensional
data

23. Example of Neural Gas
Connections are created between the best matching unit and the second closest
Connections are allowed aging and are removed eventually if not refreshed

24. SOMs for data temporal processing
 Several recent extensions of SOM for processing
data sequences that are temporally or spatially
connected
 For example: words, DNA sequences, time series
 Models differ on the notion of context, i.e. the
way they store sequences
 Each neuron is represented by a weight w i d
(codebook) vector and a context (several)
vector(s) ci d

25. Gamma Memories
 The Gamma filter is defined in the time domain
as K
y  n    k ck  n 
k 1
ck  n    ck (n  1)  (1   )ck 1  n  1
 where c0 (n)  x(n) is the input signal, y (n) is the
filter output, and k , k are the filter
parameters
 Parameter  controls the tradeoff between
depth and resolution of the filter

26. Cascade of K-stages
 A recursive rule for context descriptor of order-
K can be constructed
The K context descriptors are described as
ck (n)   ckIn1  1    ckIn1 , k
1
c0n1  wIn1
I
I n 1 : previous winner

27. Gamma SOM Map

28. Delay Coordinate Embedding
 Takens´embedding theorem allows us to
reconstruct the dynamics of an n-dimensional
space state starting by a one-dimensional time
series, e.g. strange attractor.
 To embed a time series, the following delay
coordinate vector is constructed:
s(t )   xi (t ), xi (t  t ), , xi (t  (m 1) t )
 Embedding parameters (t,m) are found by
using ad-hoc methods
 First minimum of the average mutual information (t)
 False nearest neighbor algorithm (m)

29. Gamma Filtering Embedding
 Gamma SOM construct a Gamma filtered
embedding, as follows:
u i (t )   wi (t ), c1i (t ),
 , cK (t ) 
i

 Wherew i is the weight vector and c i are the contexts
 Embedding parameters are determined by
sweeping an array of (, K) values
 Find the top 10 combinations of parameters with lower
temporal quantization errors
 Project u  t  to the principal direction by using PCA
 Search for the 1D-PCA projection (allowing for shift delays)
having maximal mutual information with the original time
series

30. Experiments
 Chaotic Lorenz System: state variable x(t )
 NH3-Far Infrared Laser:
 Data set A in the Santa Fe Time Series Competition

31. Phase Portrait for Lorenz original
dataset
Bicup 2006 challenge time series

32. Phase Portrait for noisy Lorenz dataset

33. 1D projection of Gamma SOM for noisy
Lorenz dataset

34. 2D projection of Gamma SOM for Laser
Time Series

35. Conclusions
 Gamma SOM models can reconstruct the state
space by using Gamma filtering embedding
 Useful tools for non-linear time series analysis
 Advantage of noise reduction
 Future work: Time series prediction

36. References
 Estevez, P.A., Hernandez, R.: Gamma SOM for Temporal
Sequence Processing. In: Advances in Self-Organizing
Maps, WSOM 2009, LNCS 5629, St. Augustine, FL, pp.
63-71 (2009)
 Estevez, P.A., Hernandez, R., Perez, C.A., Held, C.M.:
Gamma-filter Self-organizing Neural Networks for
Unsupervised Sequence Processing. Electronics Letters
(2011)-
 Estevez, P.A., Hernandez, R.: Gamma –filter Self-
Organizing Neural Networks for Time Series Analysis.
In: Advances in Self-Organizing Maps, WSOM 2011,
LNCS 5629, Espoo, Finland, pp. 63-71 (2011)
 Estevez, P.A. and Vergara, J.: Nonlinear Time Series
Analysis by Using Gamma Growing Neural Gas, WSOM
2012, Santiago, Chile (in press)

38. ALMA Site in Northern Chile