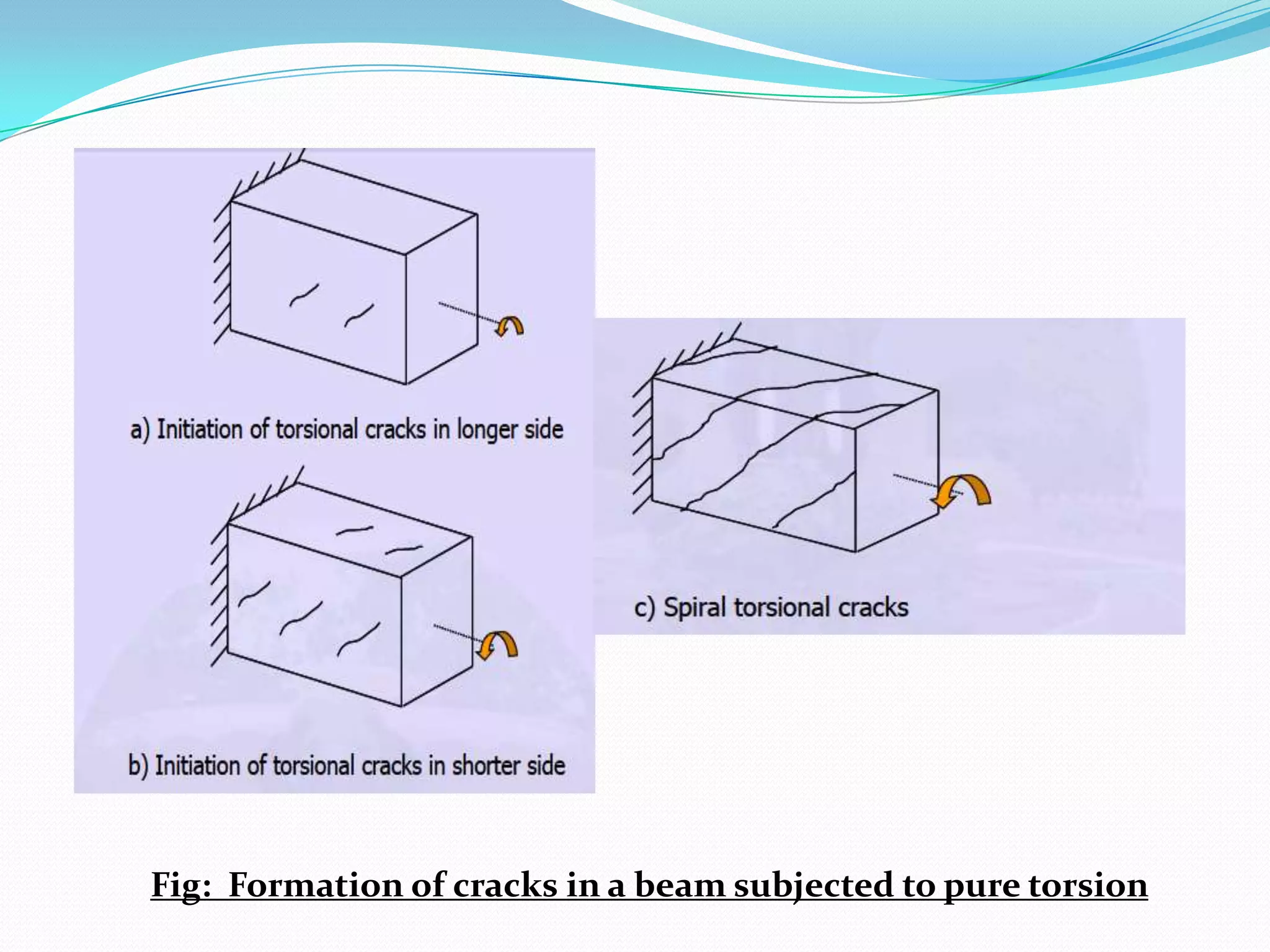
This document discusses torsional stress and its effects on beams and circular shafts. It makes the following key points: 1. Torsional stress is the shear stress developed in a material subjected to a twisting torque, and is highest at the outermost parts of the material furthest from the central axis. 2. Cracks form under torsional stress and initially appear at the middle of the longest side of a beam, then the shortest side, before circulating around the beam's periphery. 3. Failure of brittle materials under pure torsion occurs along planes inclined to the beam axis, not perpendicular, due to elastic theory principles.

1. AHSANULLAH UNIVERSITY OF SCIENCE & TECHNOLOGY
Name: Mehedi hossain
Student I.D. : 10.01.03.092
Section: B

2. TORSIONAL STRESS

3. Torsion is a twisting moment that is applied on an object by twisting
one end when the other is held in position or twisted in the opposite
direction.

4. Torsion
 For the purpose of deriving a simple theory to describe the







behavior of shafts subjected to torque it is necessary make the
following base assumptions.
Assumption:
(i) The materiel is homogenous i.e. of uniform elastic properties
exists throughout the material.
(ii) The material is elastic, follows Hook's law, with shear stress
proportional to shear strain.
(iii) The stress does not exceed the elastic limit.
(iv) The circular section remains circular
(v) Cross section remain plane.
(vi) Cross section rotate as if rigid i.e. every diameter rotates
through the same angle.

5. Torsional Stress
 Shear stress developed in a material subjected to a specified torque in torsion
test. It is calculated by the equation:
 where T is torque, r is the distance from the axis of twist to the outermost fiber
of the specimen, and J is the polar moment of inertia.
Fig: The shear stress distribution about neutral axis.

6. Torsional stress
 highest tortional shear stress will be at farthest away from center. At the
center point, there will be no angular strain and therefore no tortional
shear stress is developed.

7. Distribution of shear stresses in circular Shafts
subjected to torsion :
This states that the shearing stress varies directly as the distance ‘r' from the axis of
the shaft and the following is the stress distribution in the plane of cross section
and also the complementary shearing stresses in an axial plane.

8. Torsional stress acting in
Uncracked Beam
 The variations of the torsional shear stress (τ) along radial
lines in the cross-section are shown. It can be observed that
the maximum shear stress (τ max) occurs at the middle of
the longer side.
Fig: Beam subjected to pure torsion

9. Crack Pattern under torsional
stress
 The cracks generated due to pure torsion follow the path of principal
stress. The first cracks are observed at the middle of the longer side.
Next, cracks are observed at the middle of the shorter side . After the
cracks connect, they circulate along the periphery of the beam.

10. Fig: Formation of cracks in a beam subjected to pure torsion

11. Mode of failure due to torsional stress
 For
a
homogenous
beam
made
of
brittle
material, subjected to pure torsion, the observed plane of
failure is not perpendicular to the beam axis, but inclined
at an angle. This can be explained by theory of elasticity. A
simple example is illustrated by applying torque to a piece
of chalk
Fig: Failure of a piece of chalk under torque

12. Effect of Prestressing Force
 In presence of prestressing force, the cracking occurs at higher load.
This is evident from the typical torque versus twist curves for sections
under pure torsion. With further increase in load, the crack pattern
remains similar but the inclinations of the cracks change with the
amount of prestressing. The following figure shows the difference in
the torque versus twist curves for a non-prestressed beam and a
prestressed beam.
Fig: Torque versus Twist curves

13. FOR YOUR ATTENTION!