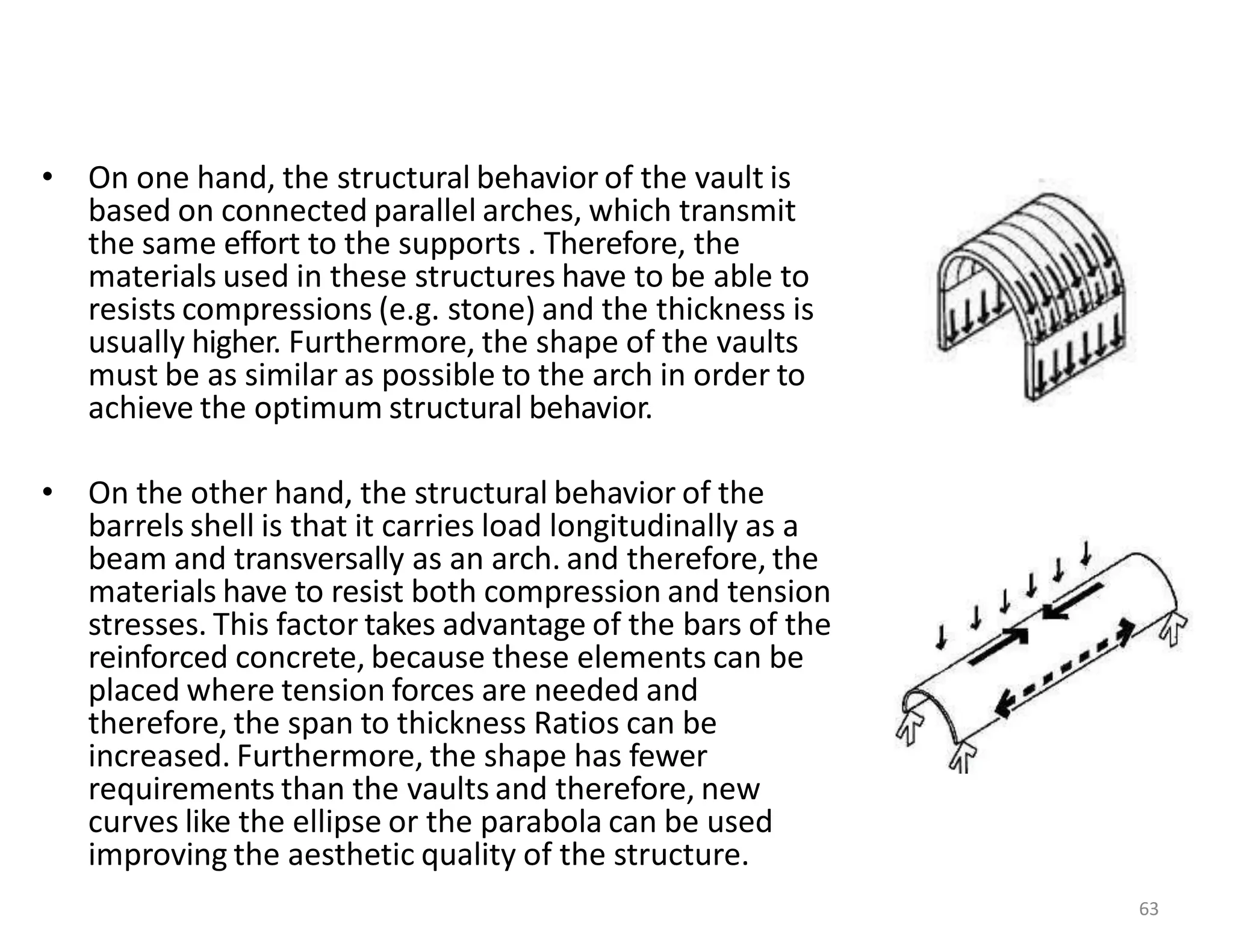
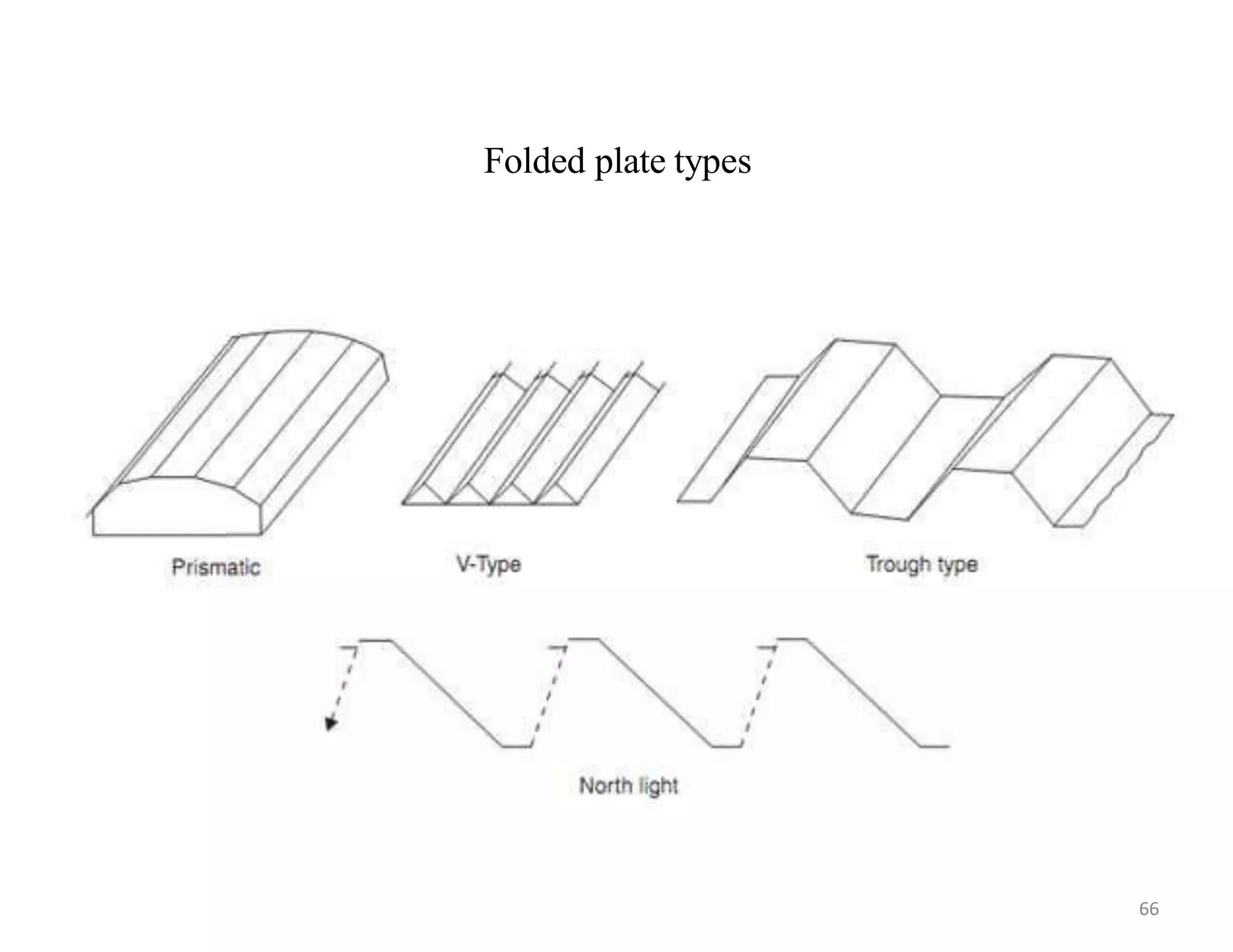
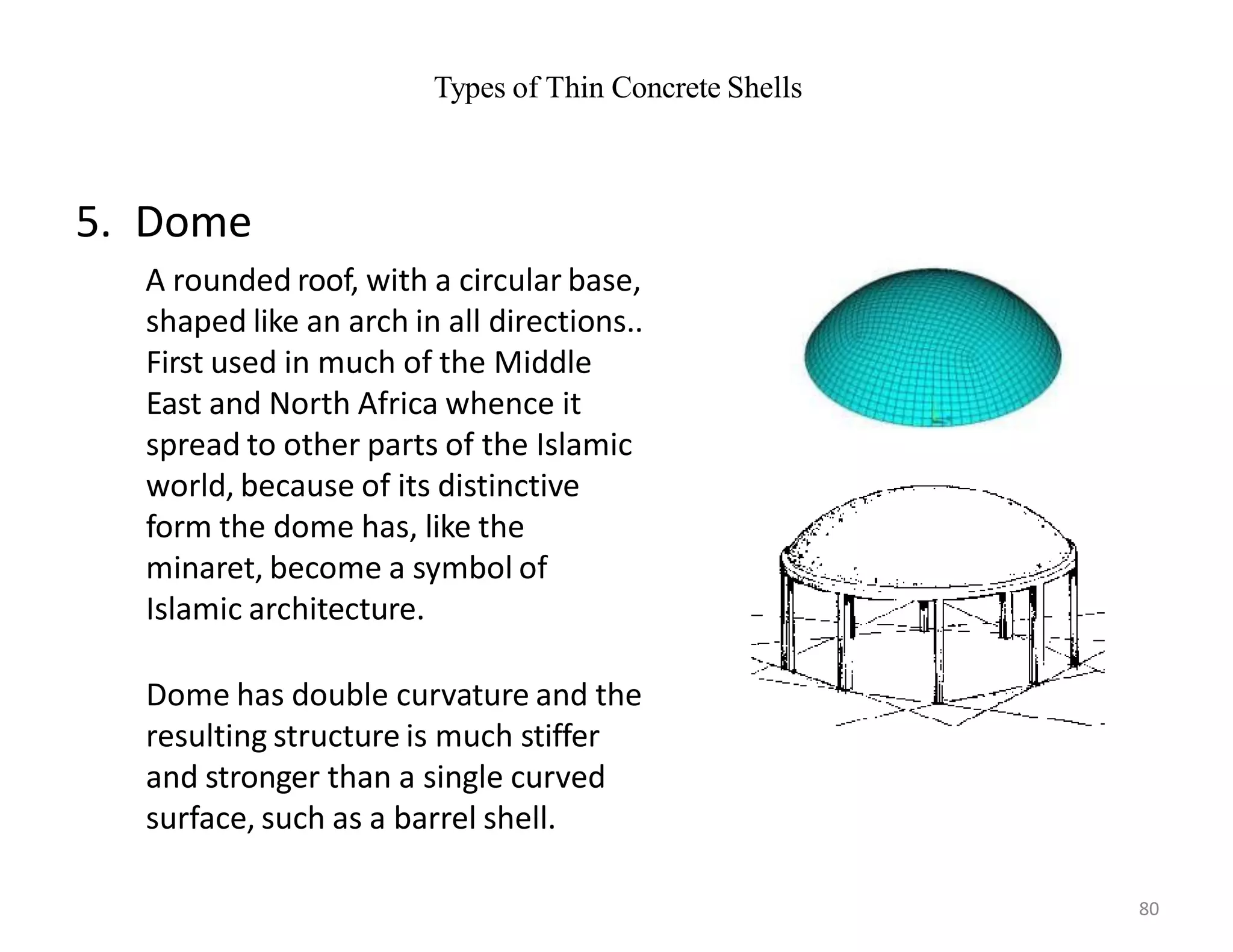
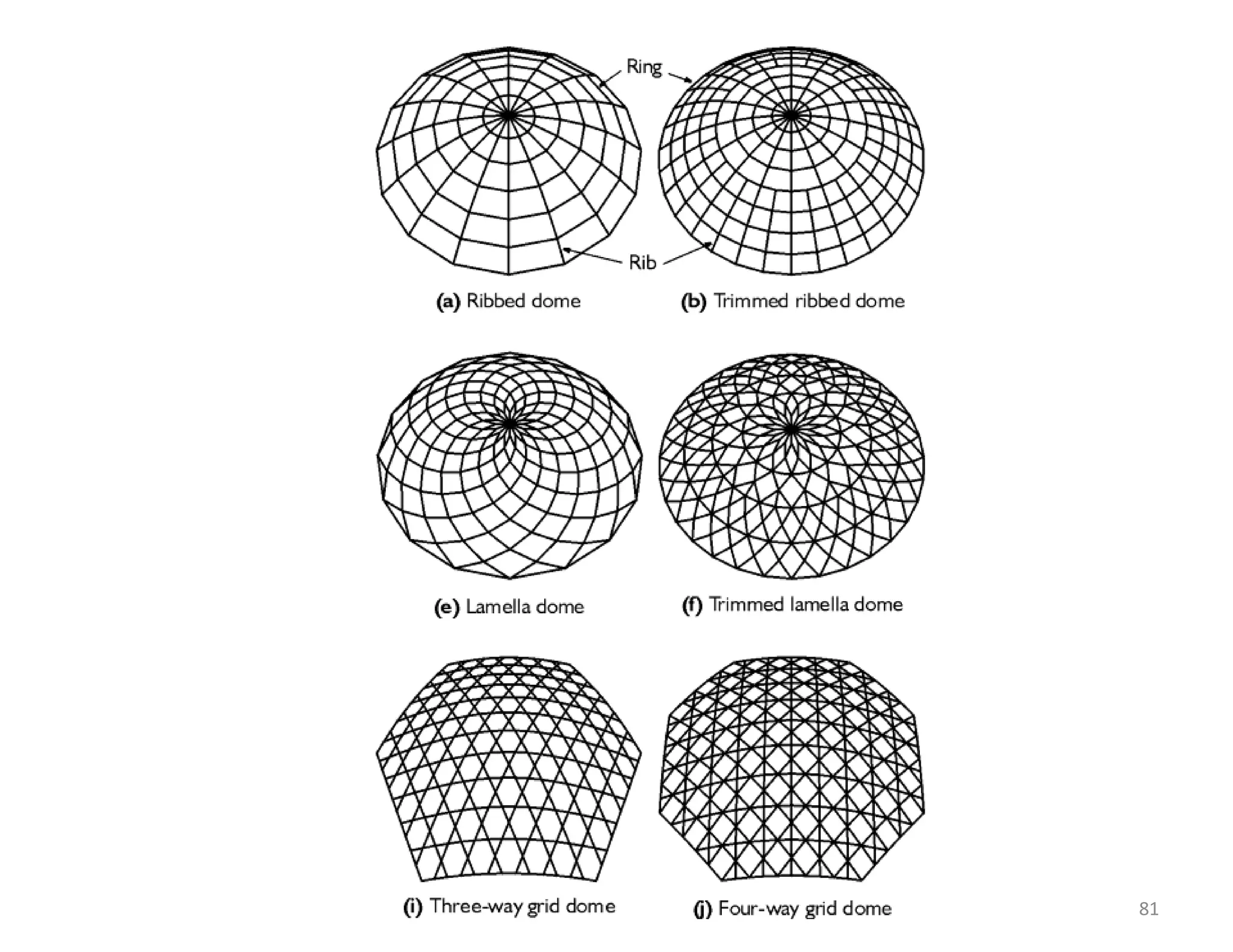
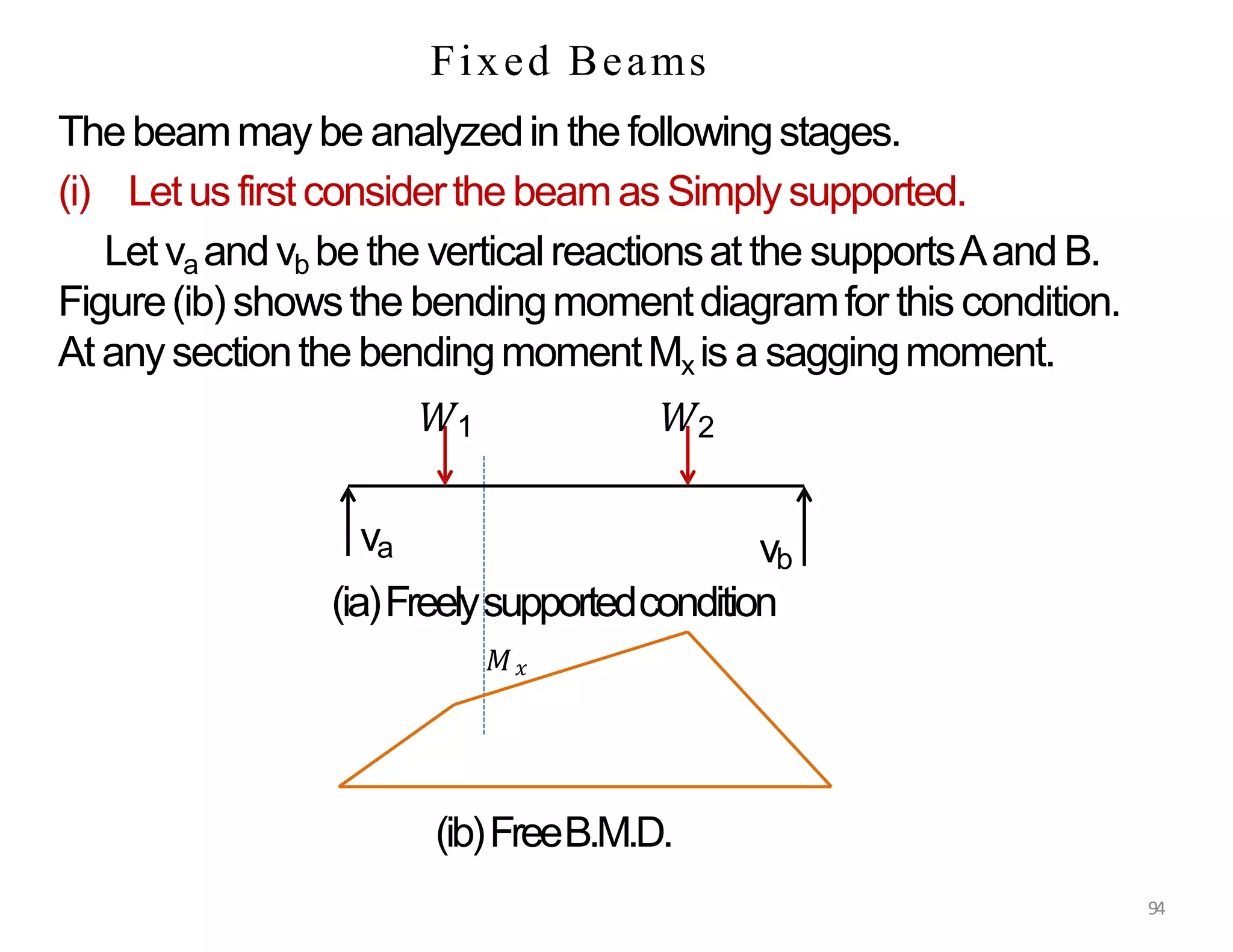
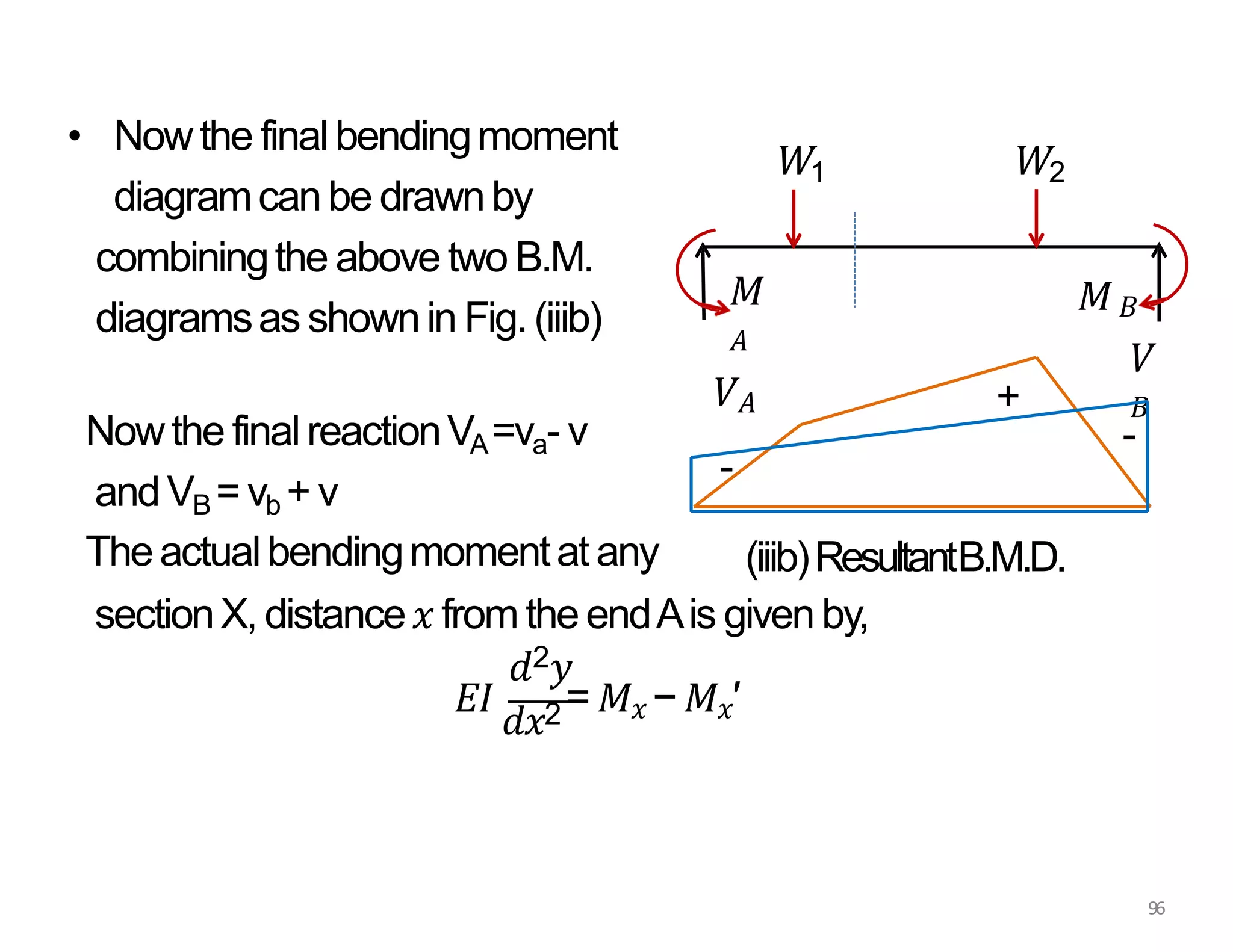
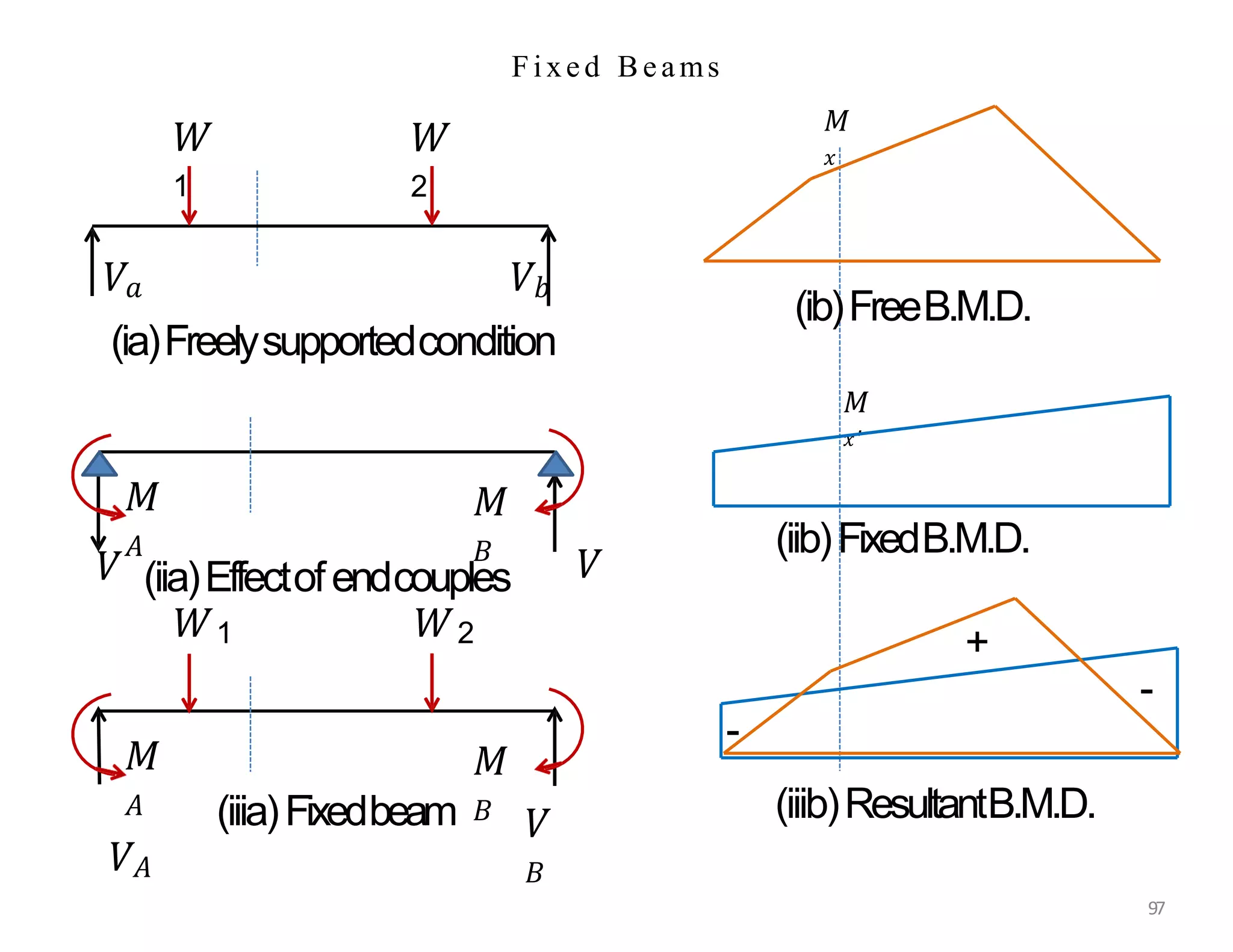
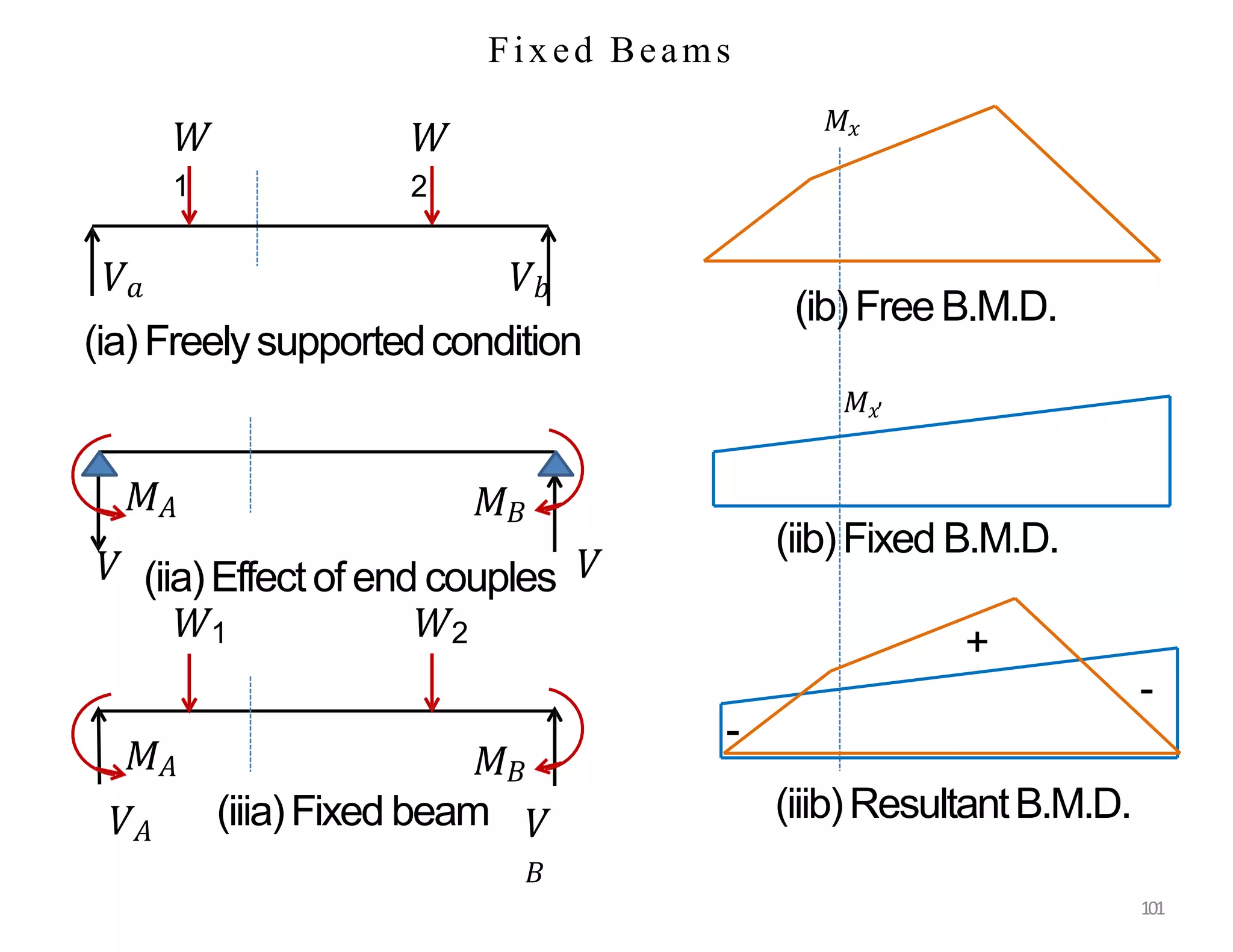
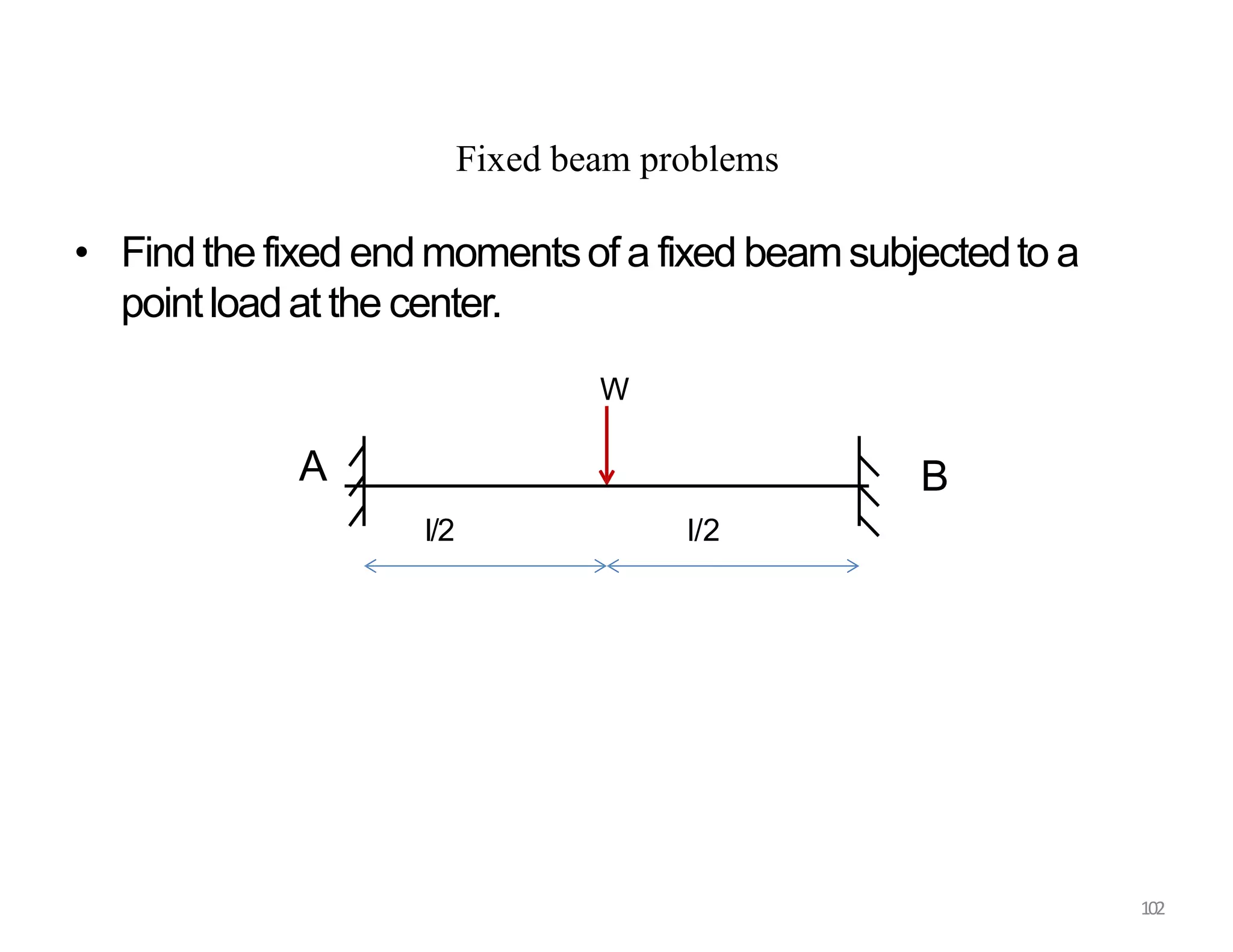
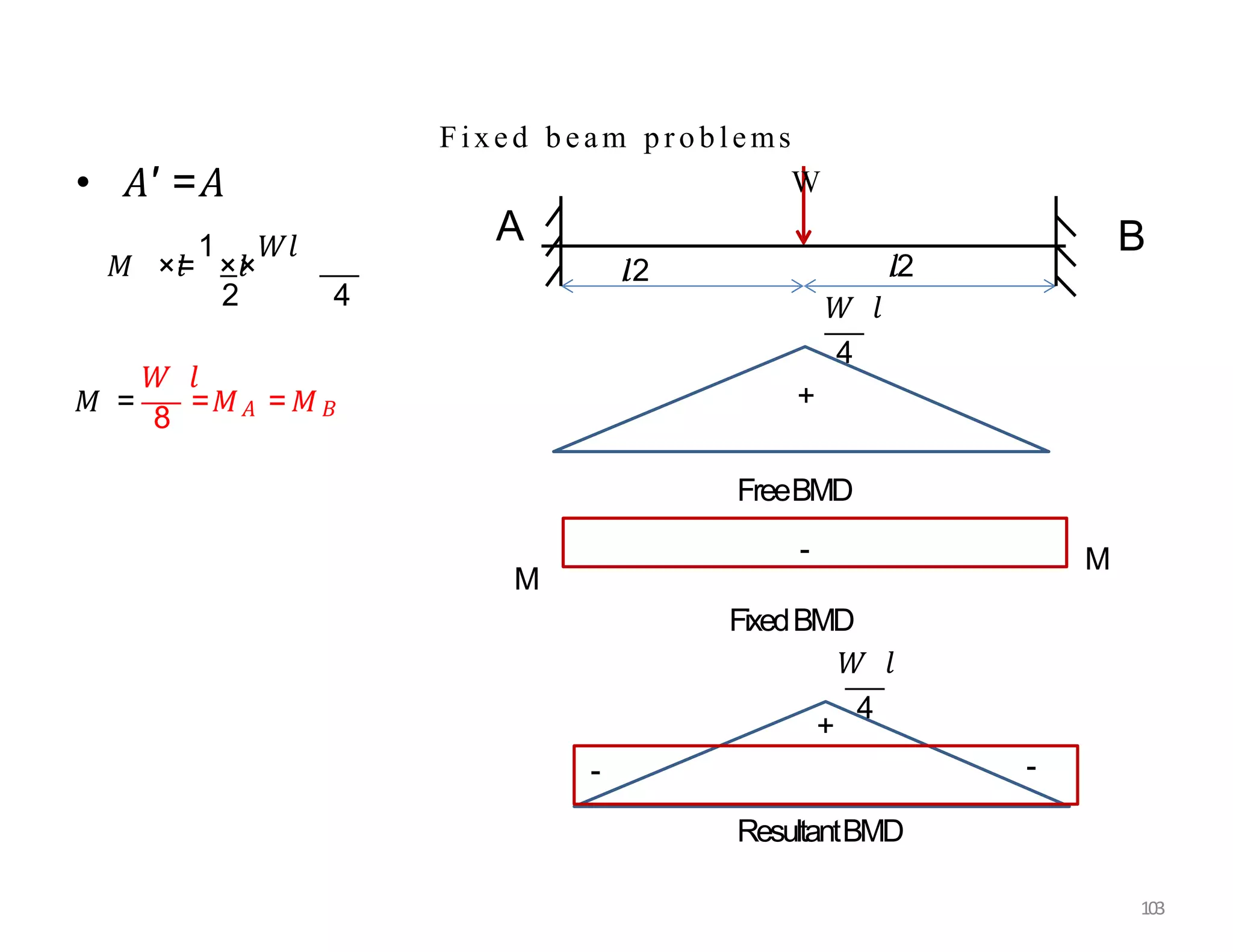
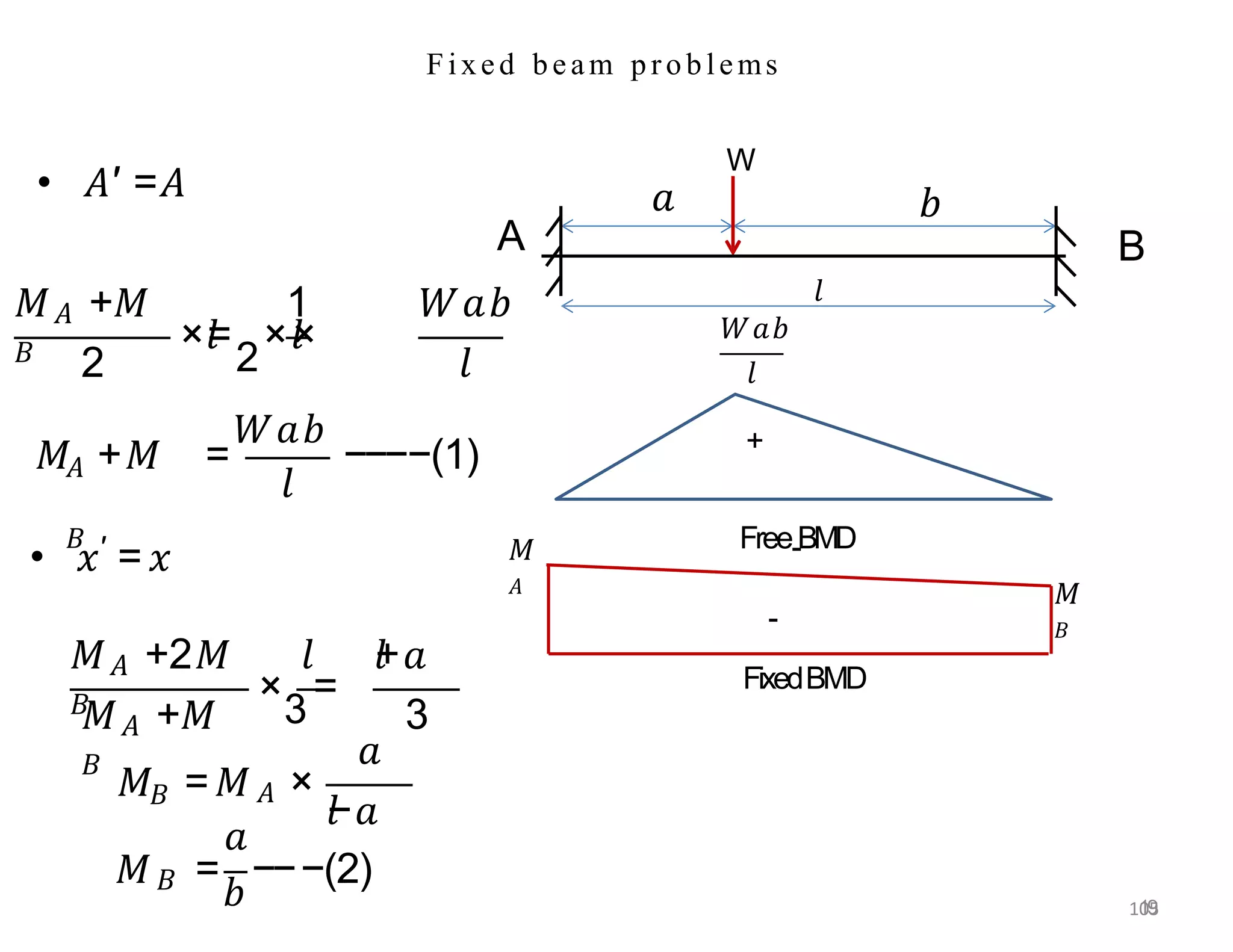
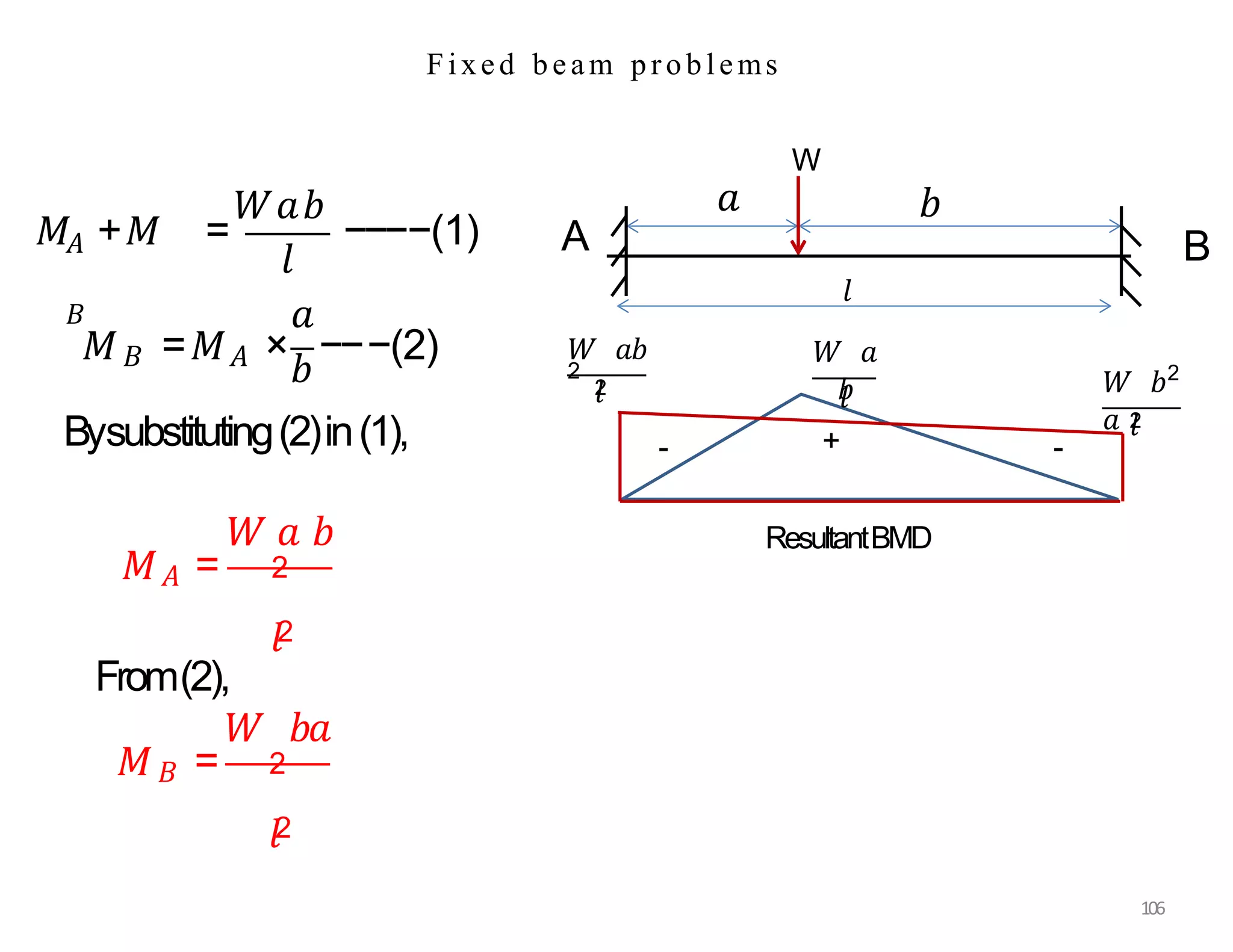
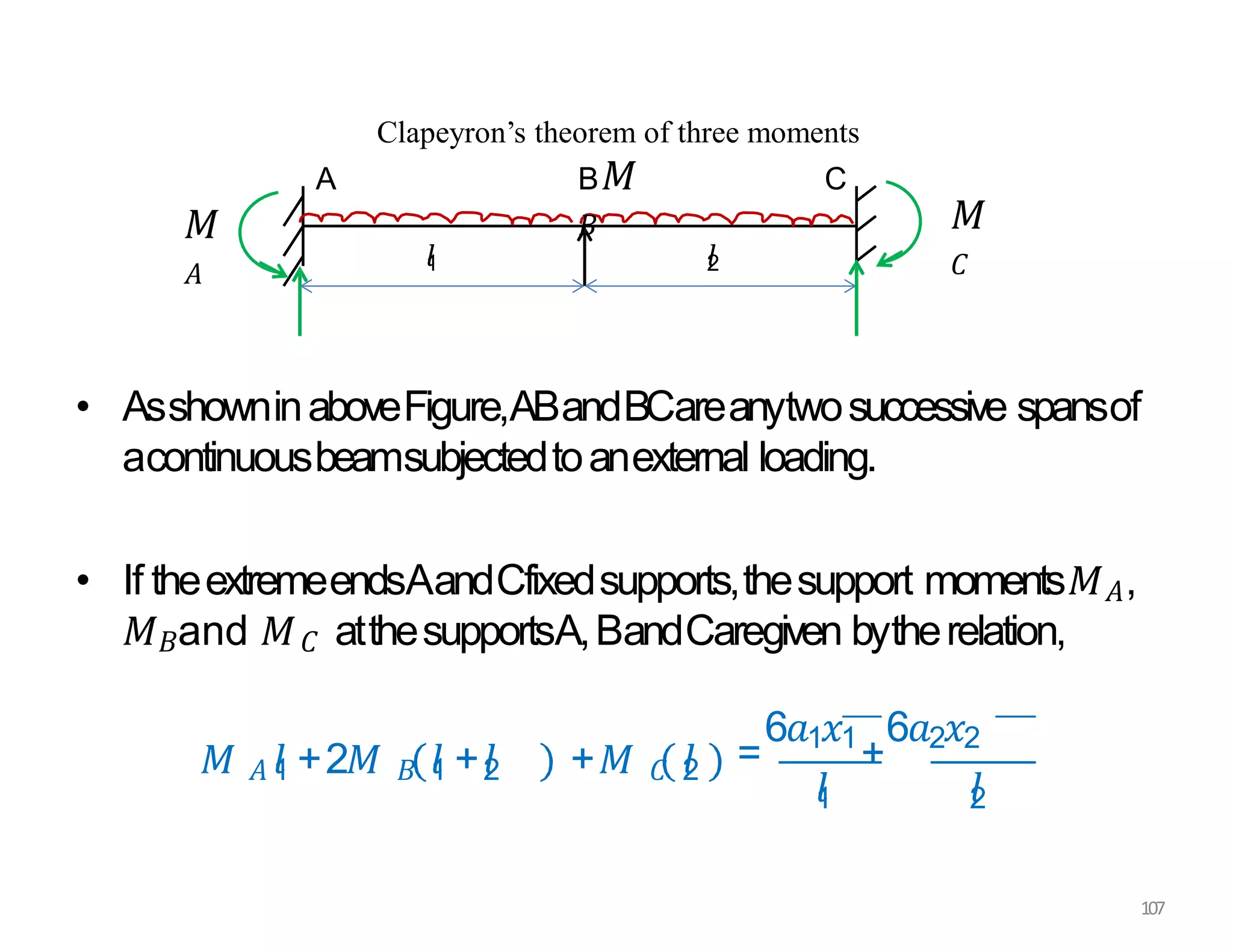
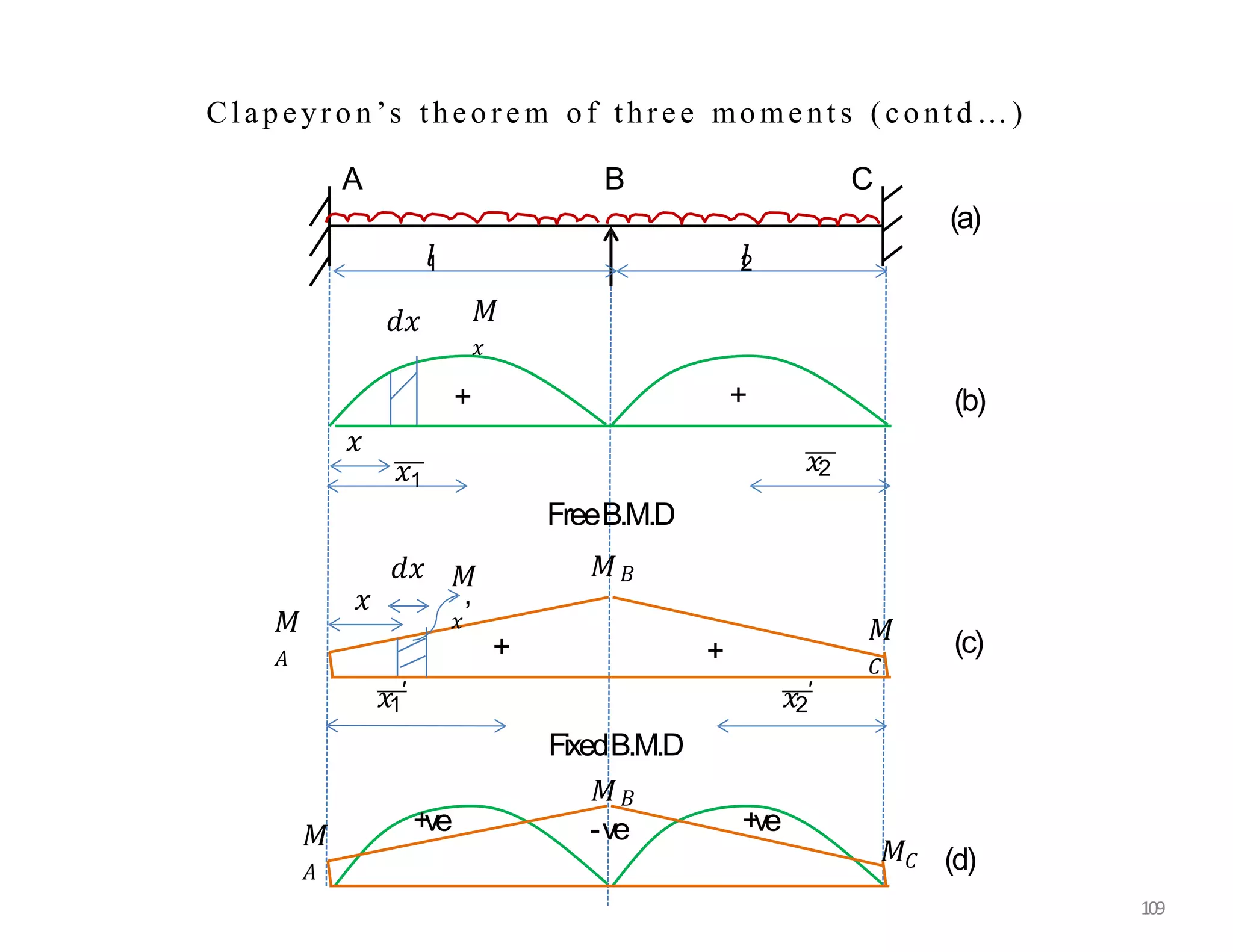
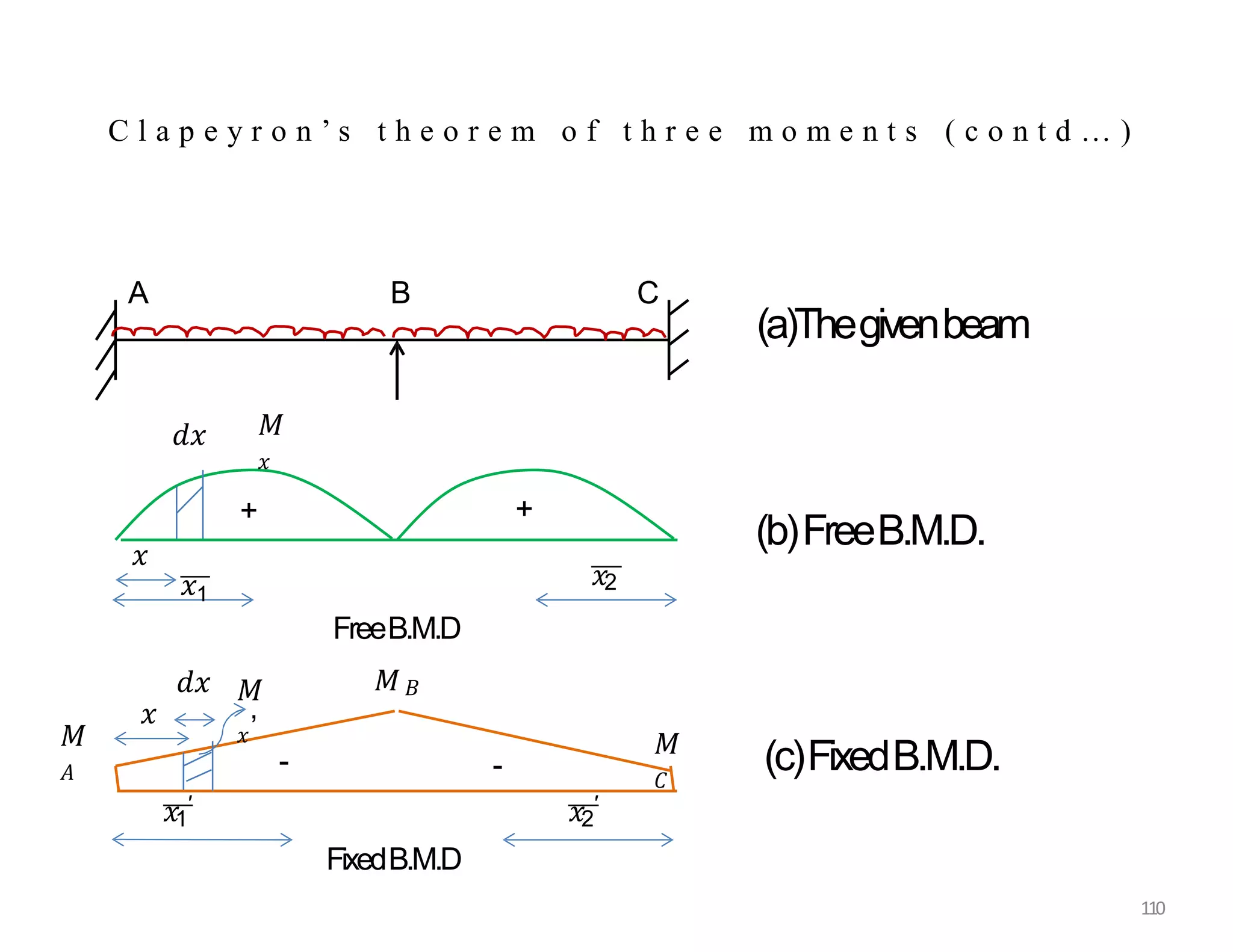
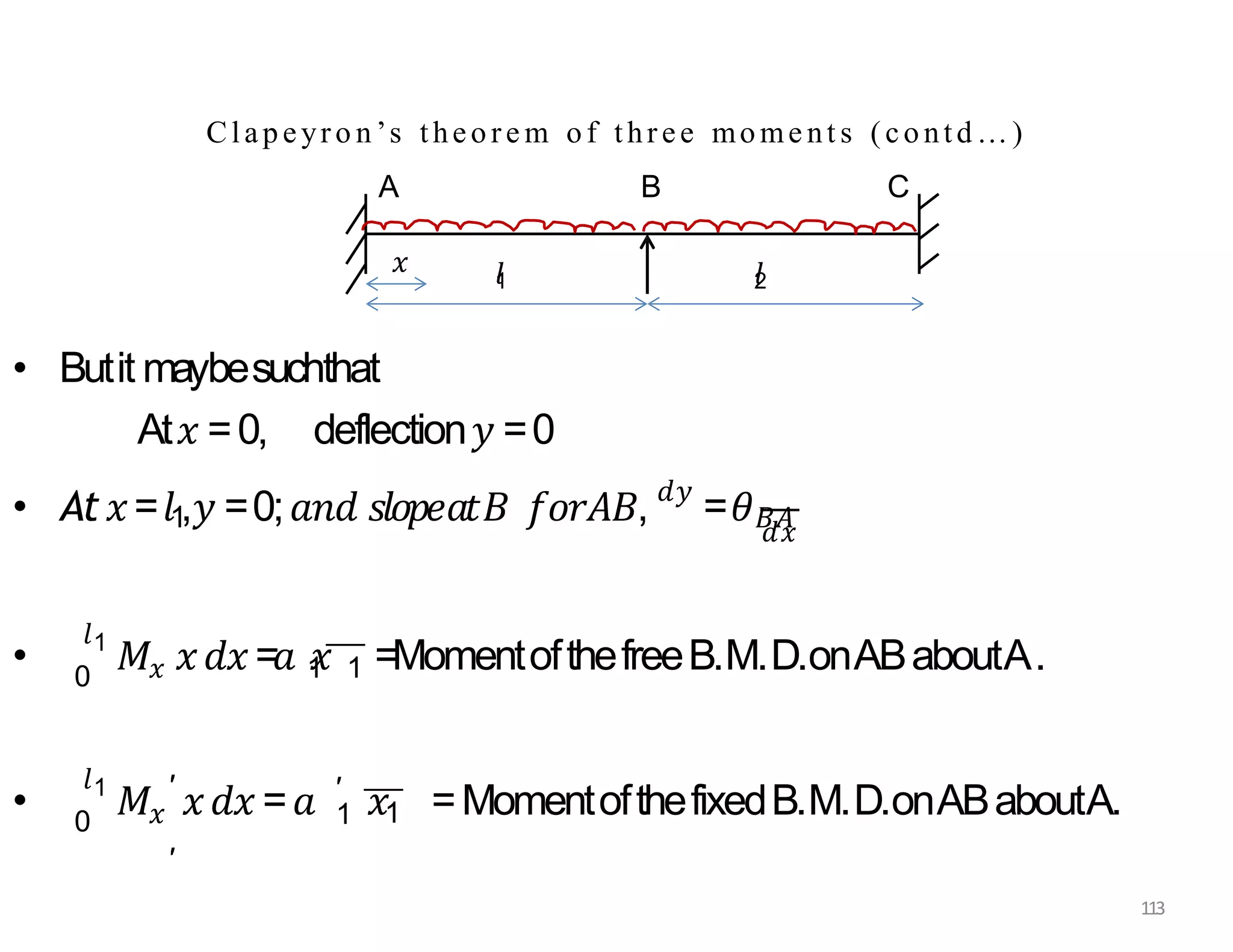
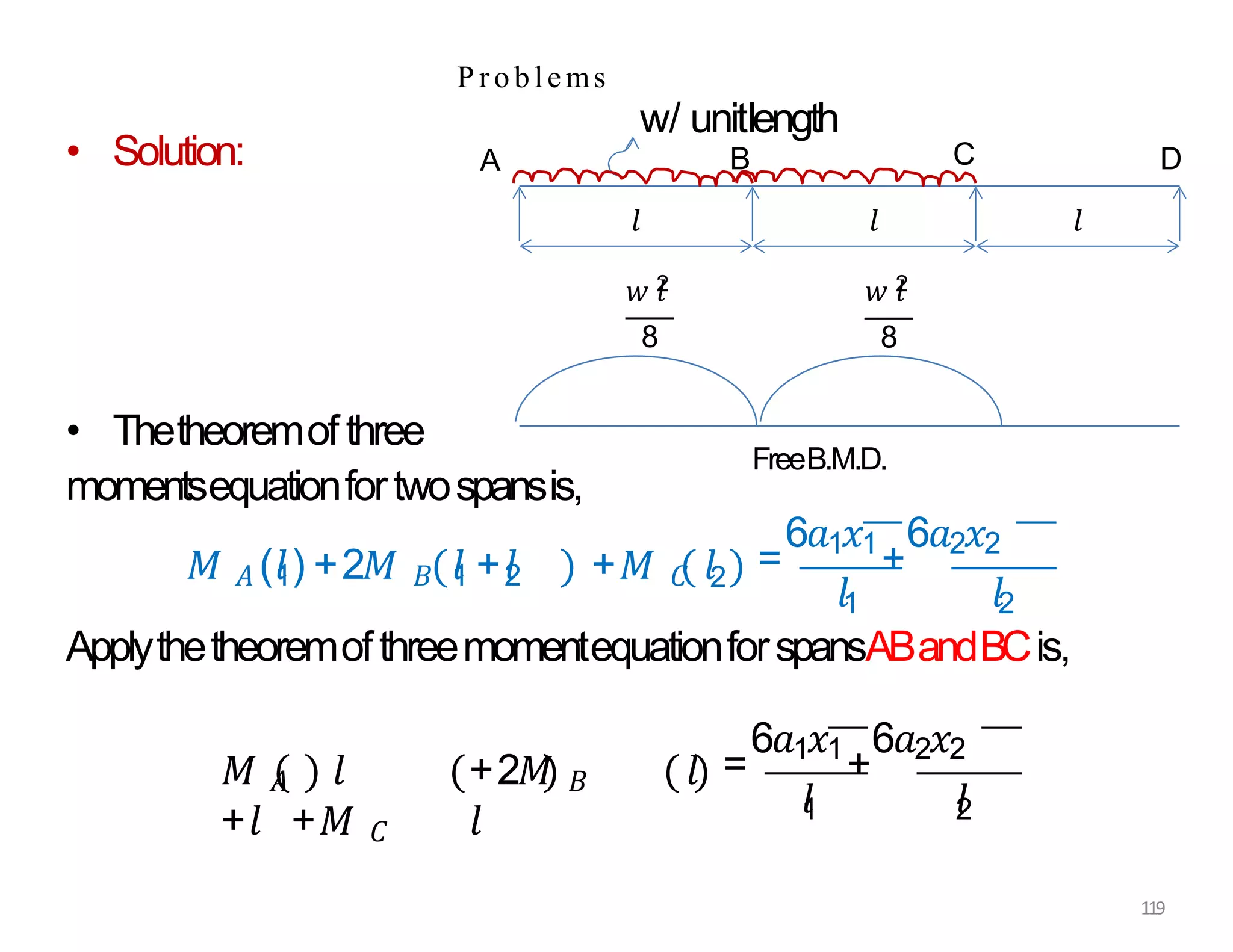
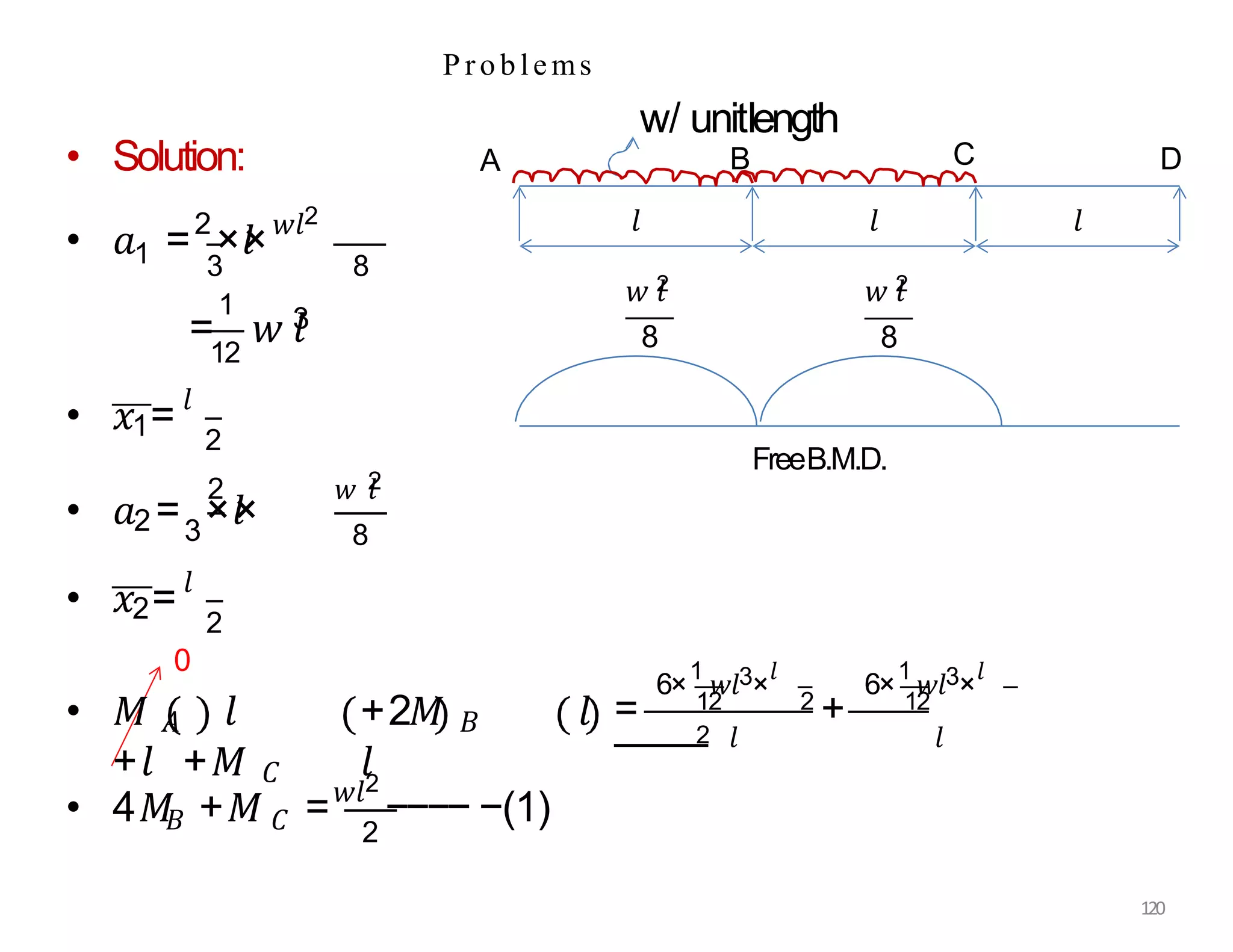
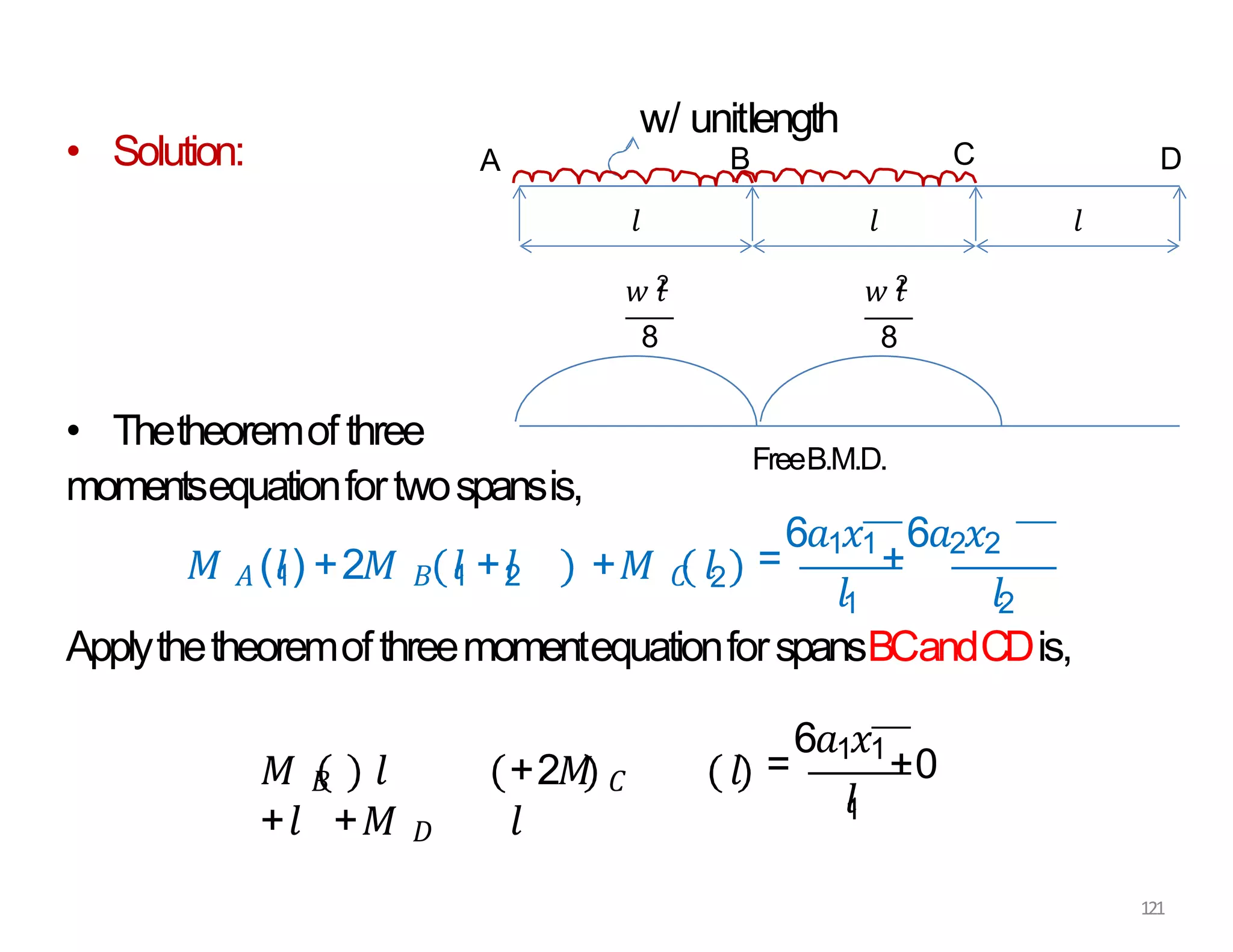
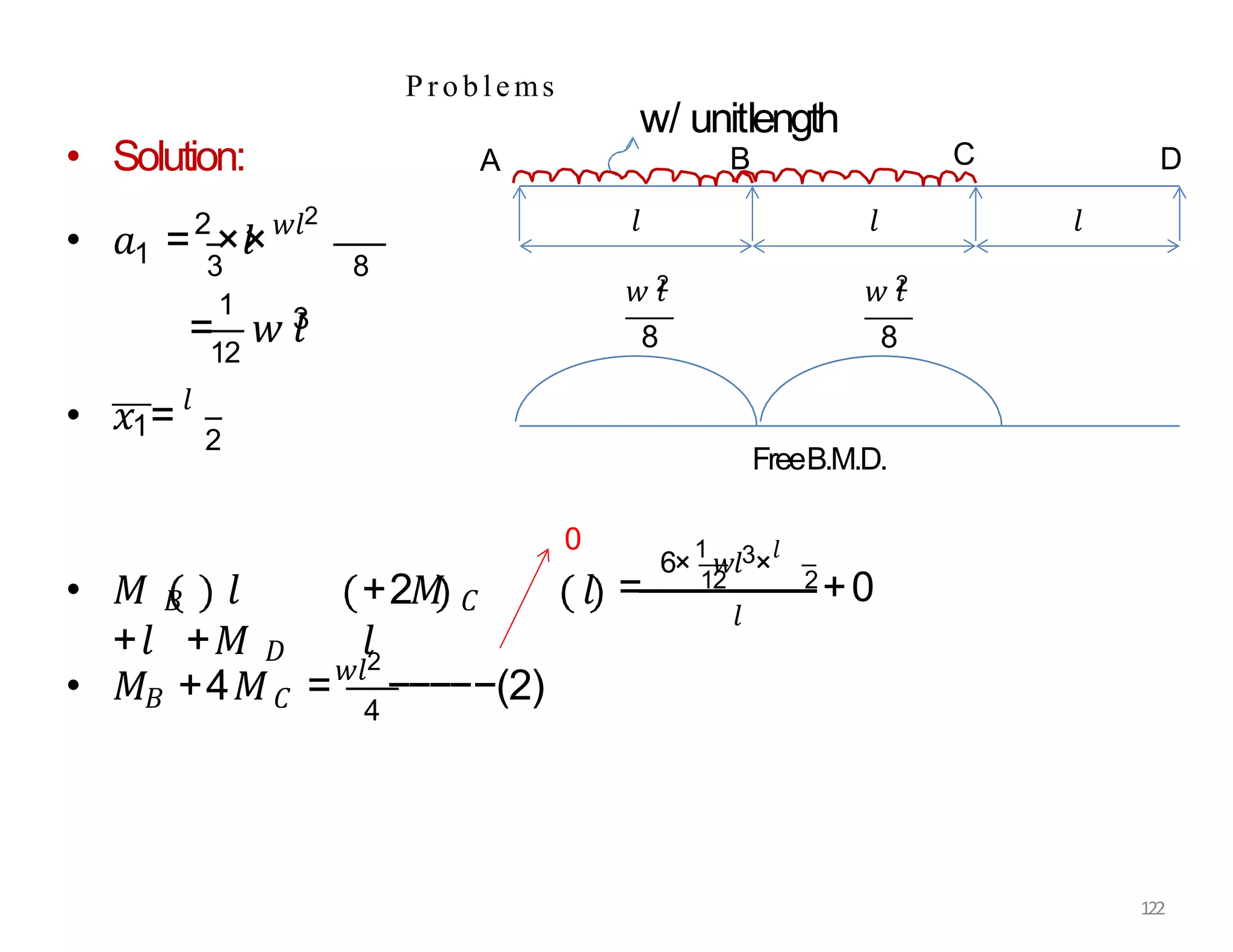
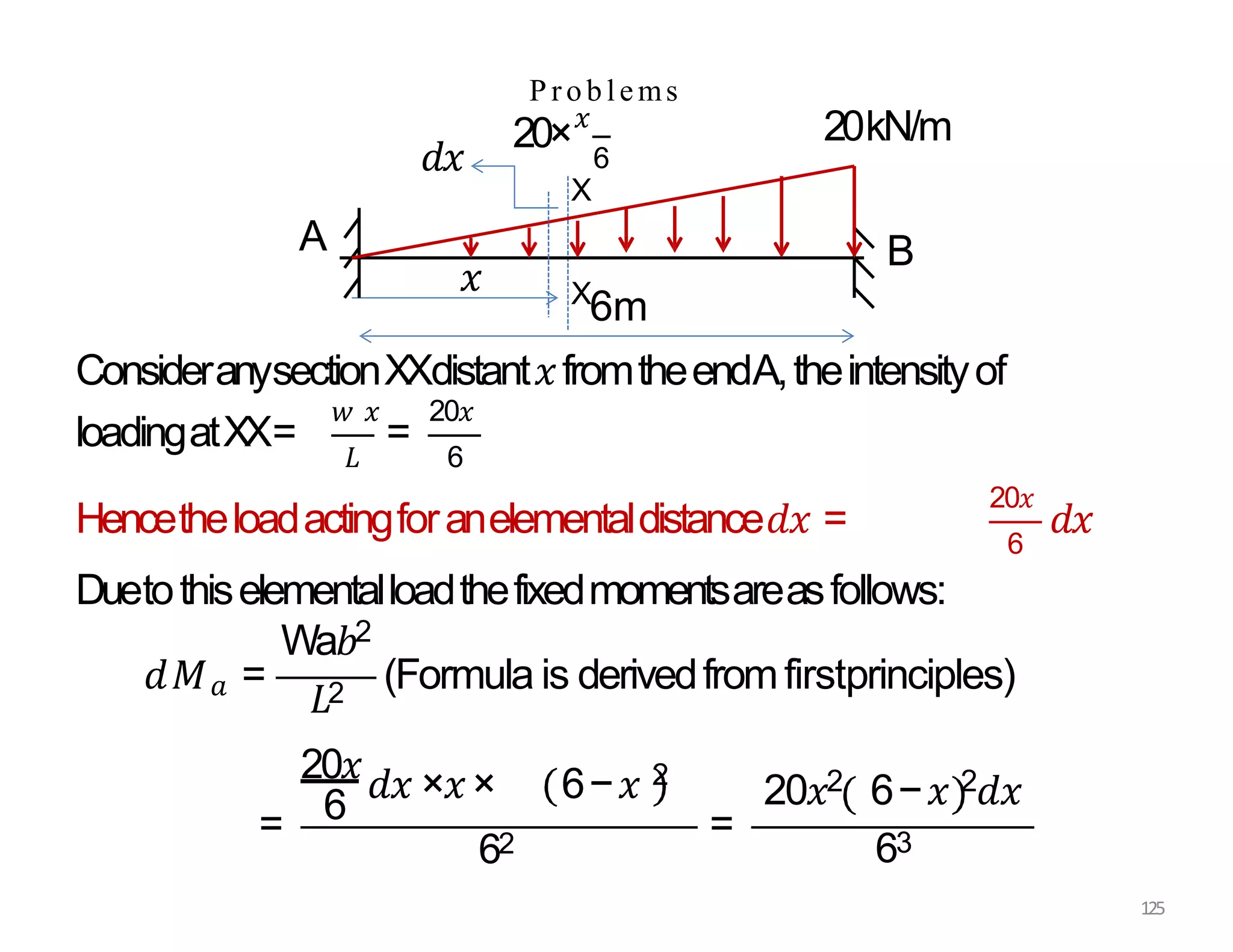
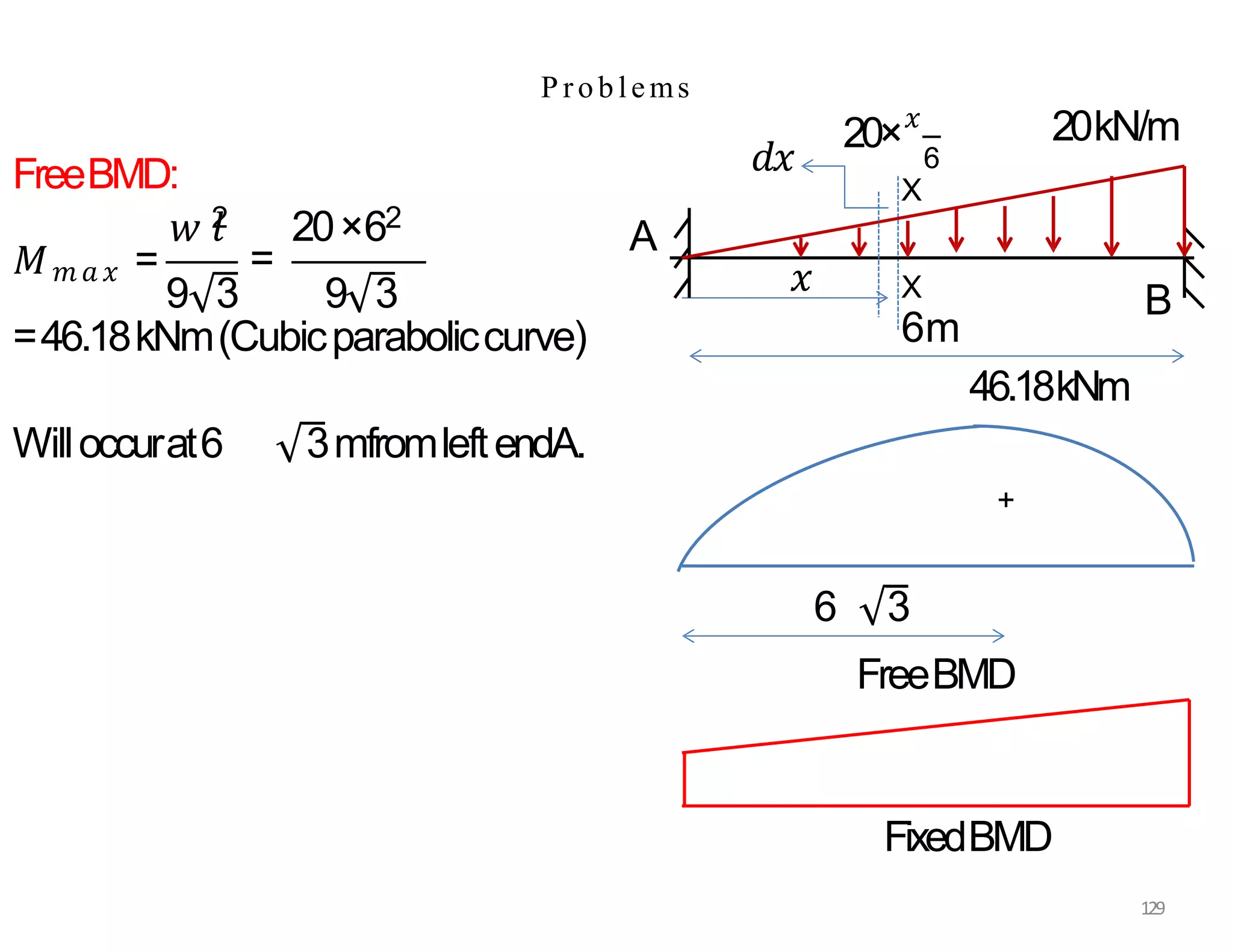
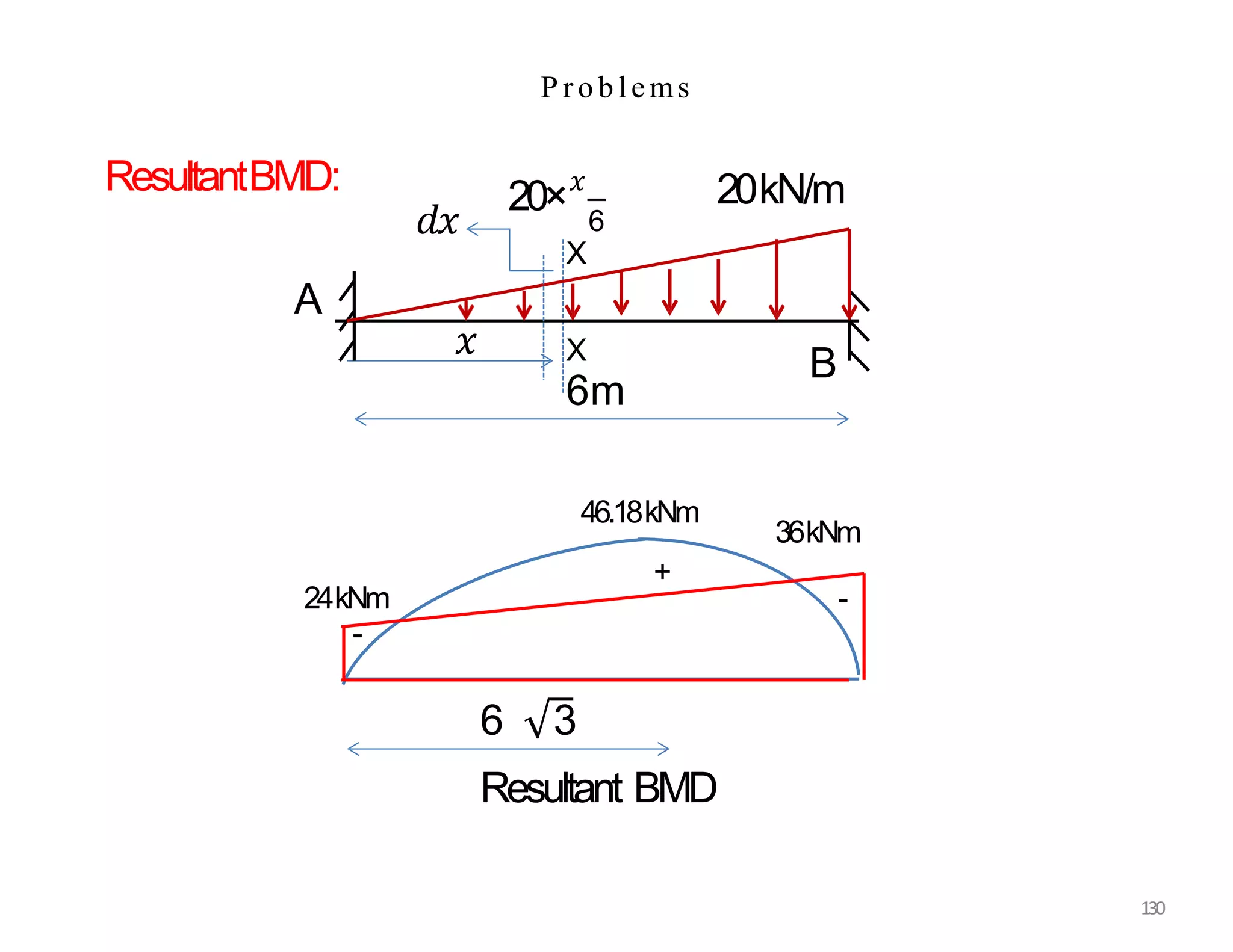
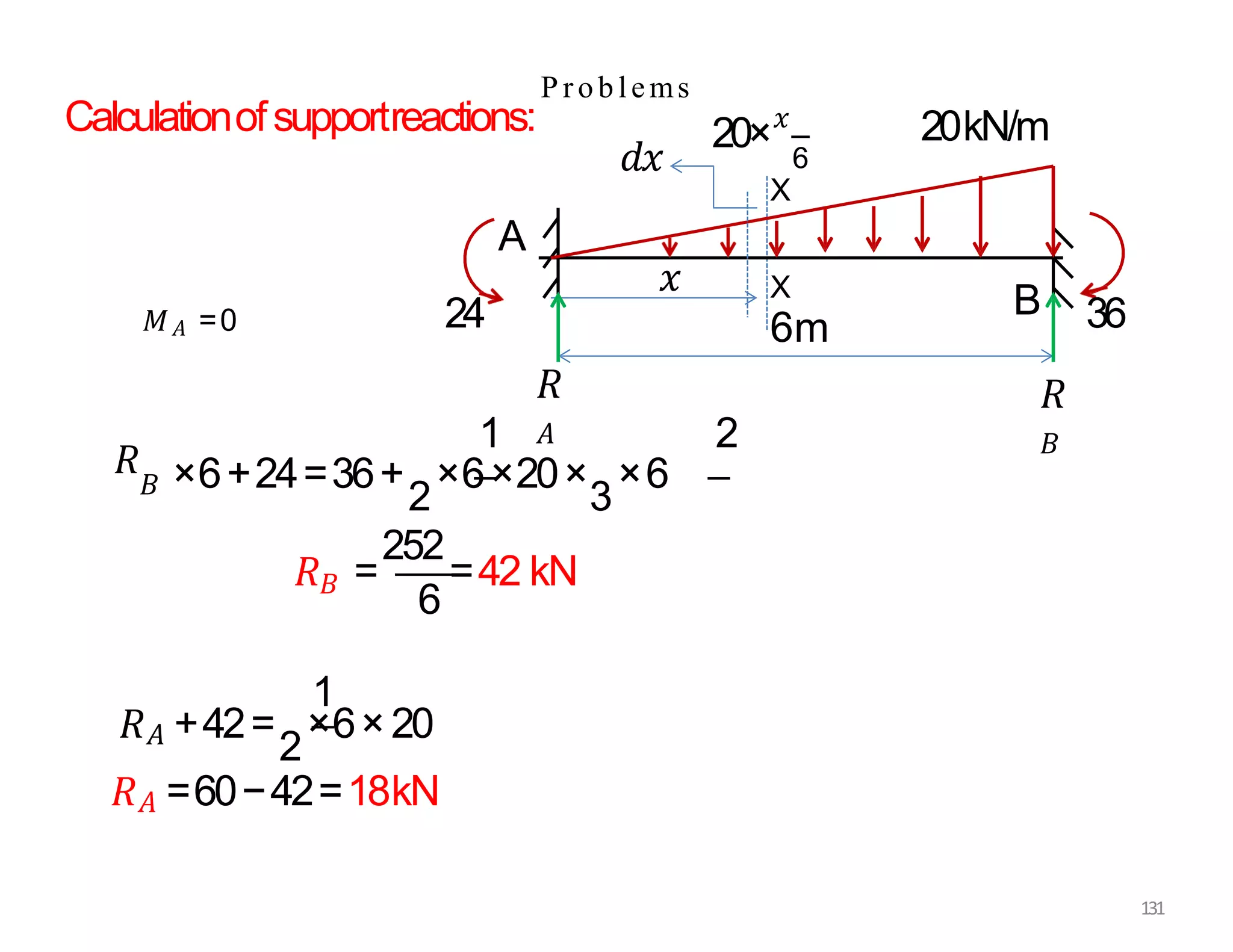
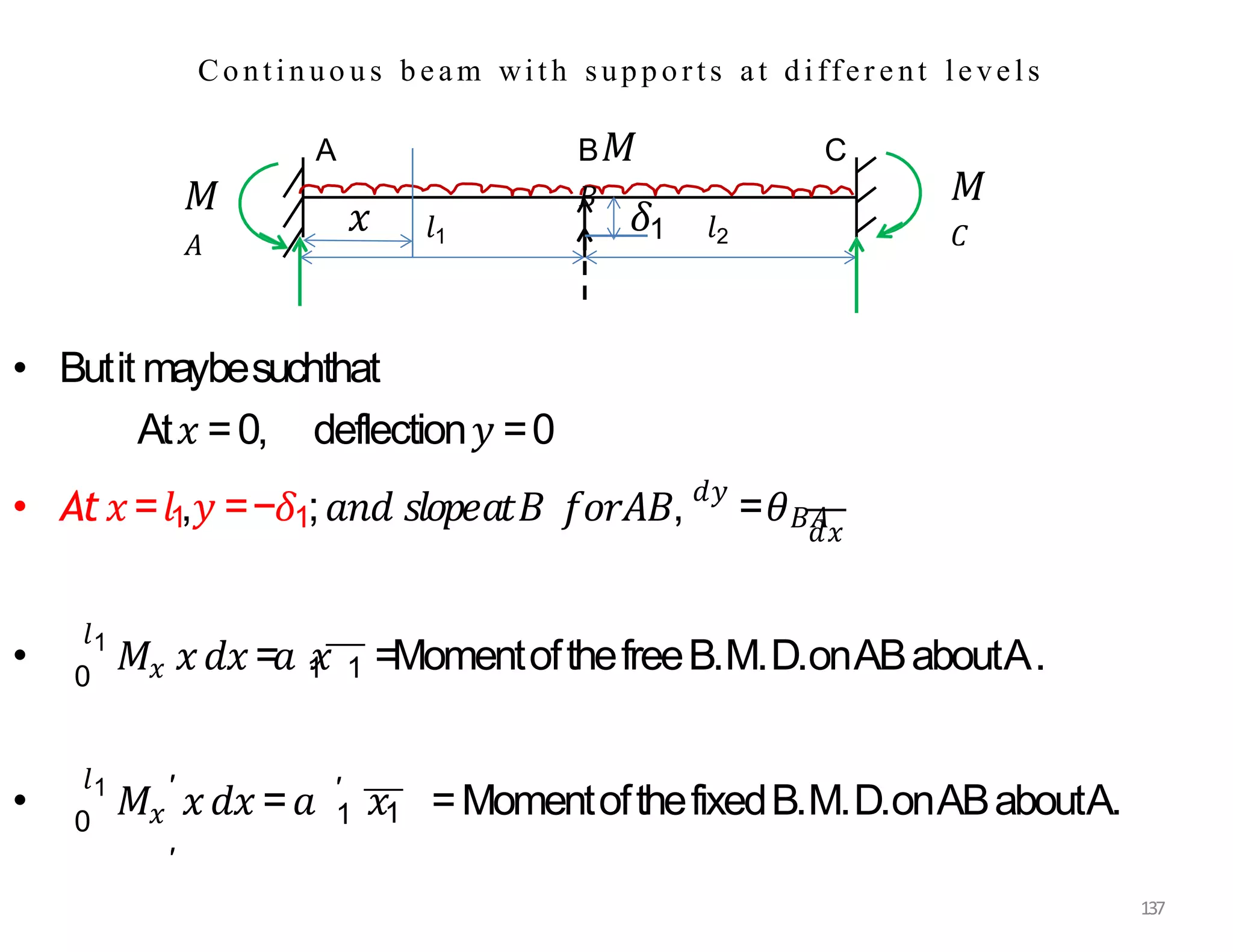
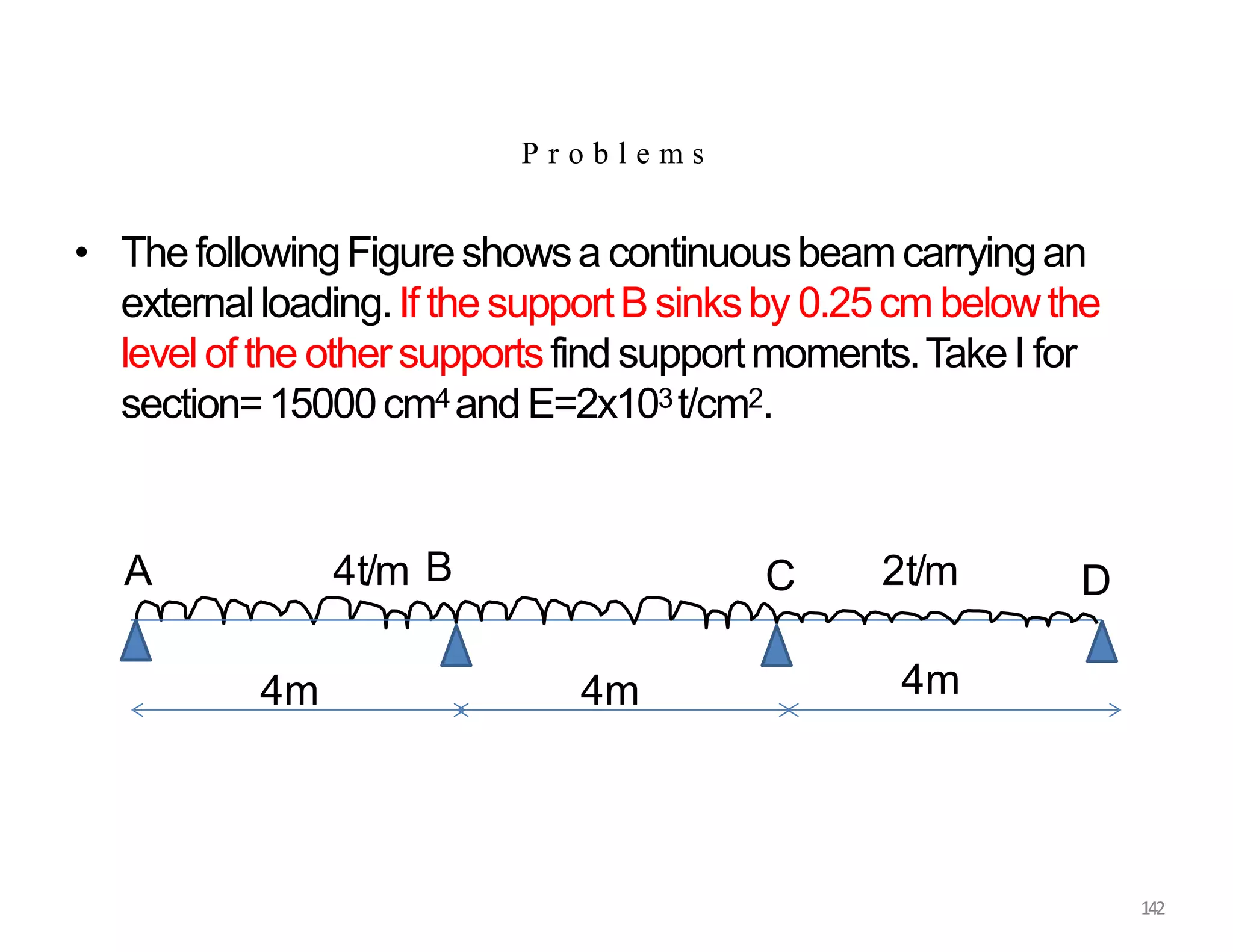
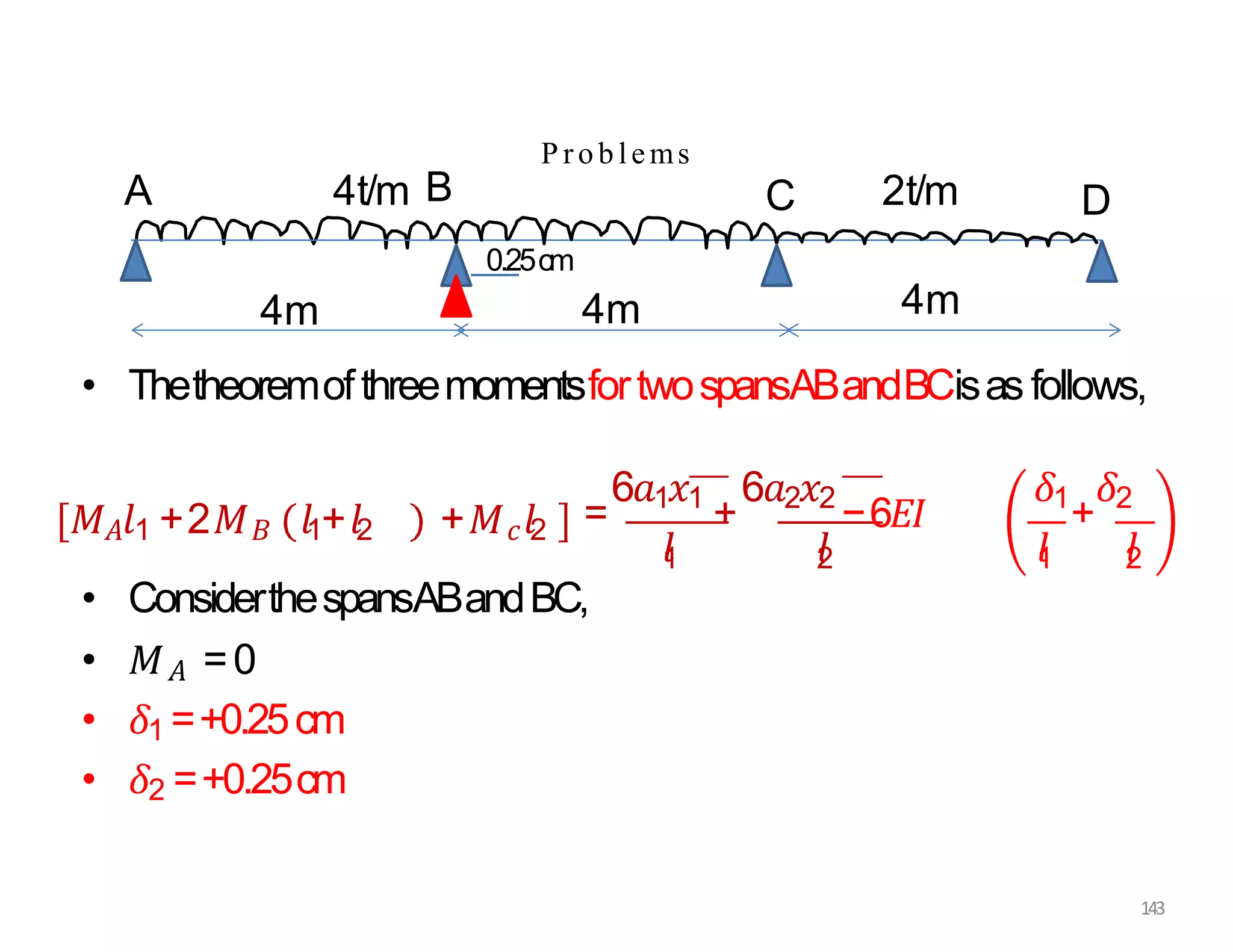
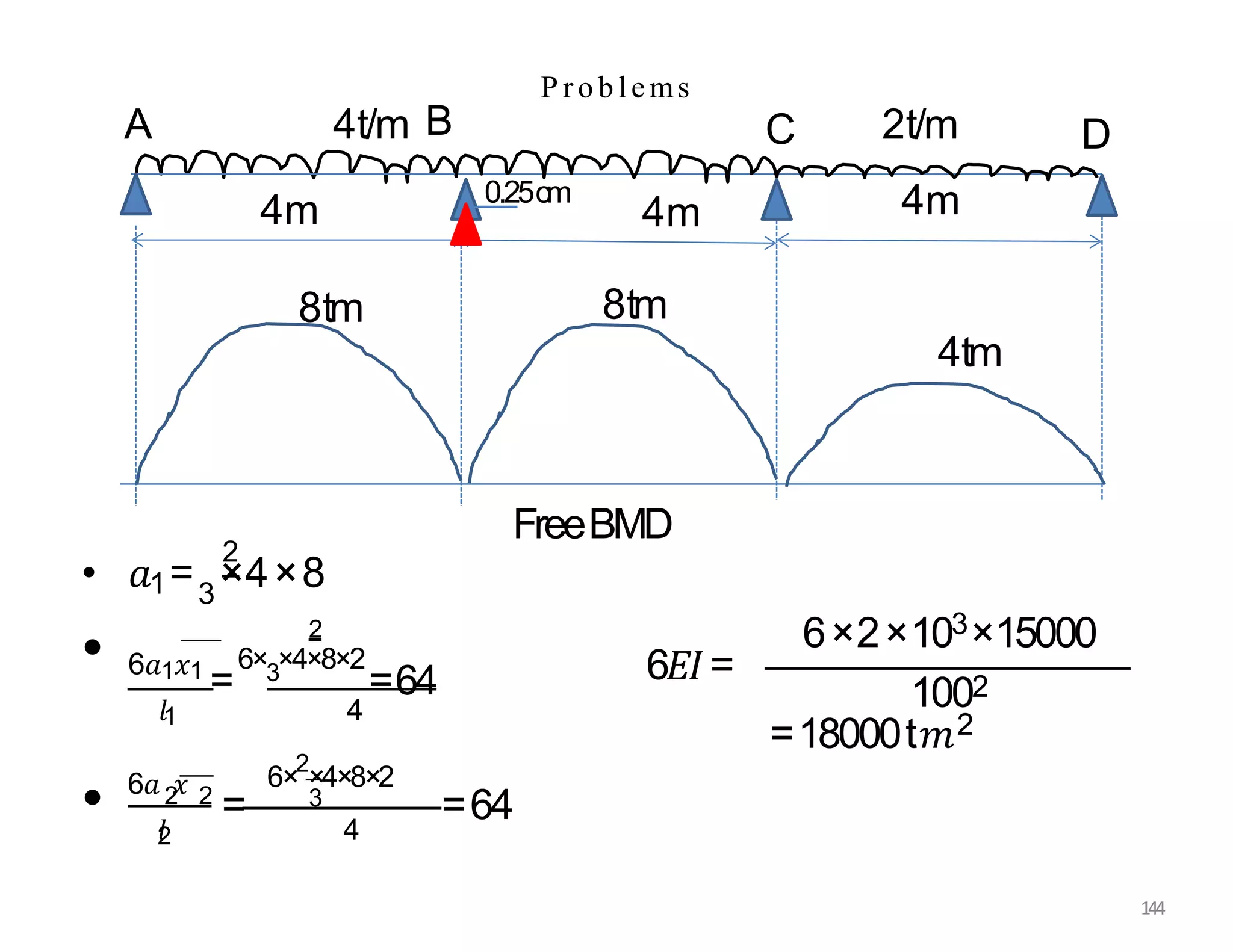
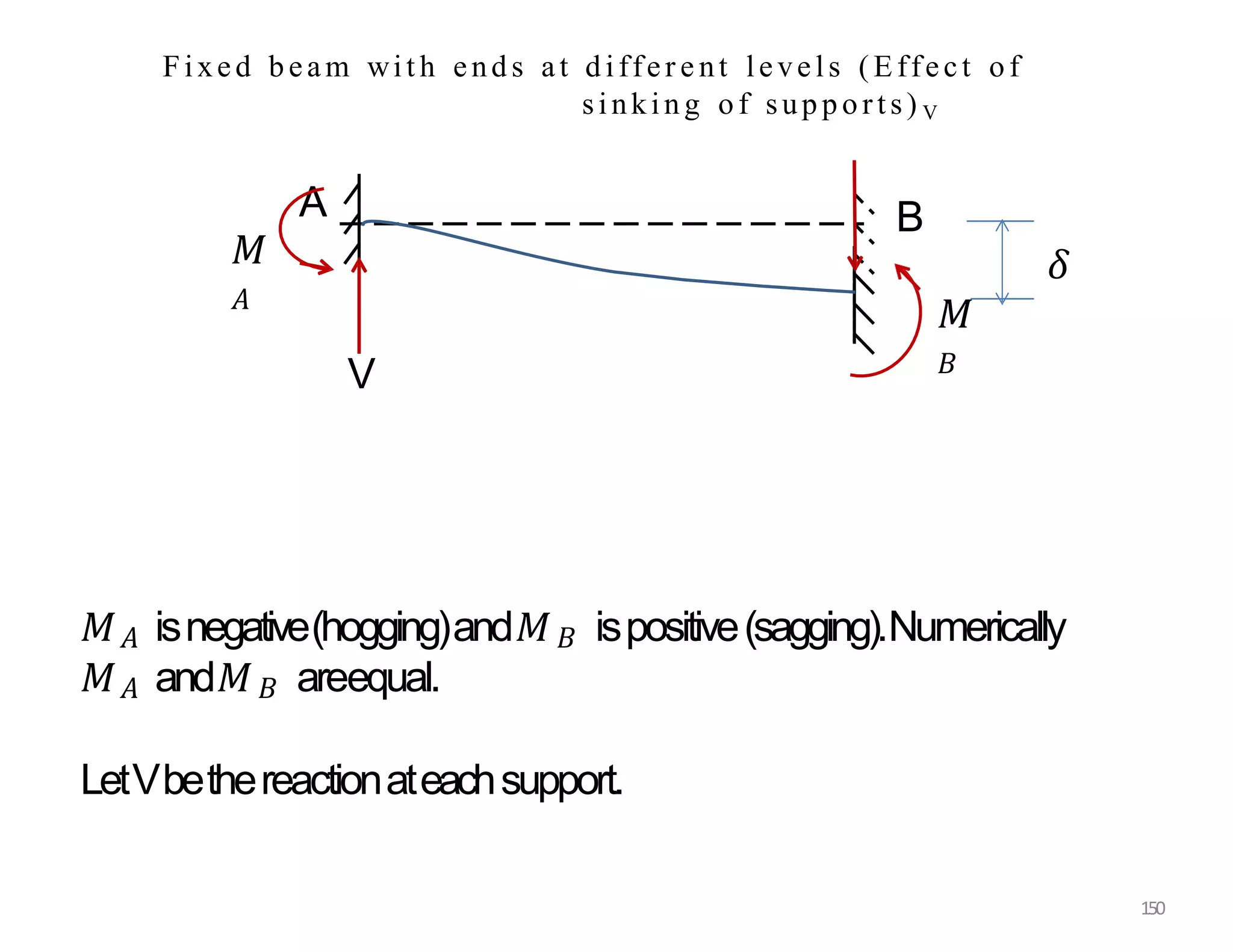
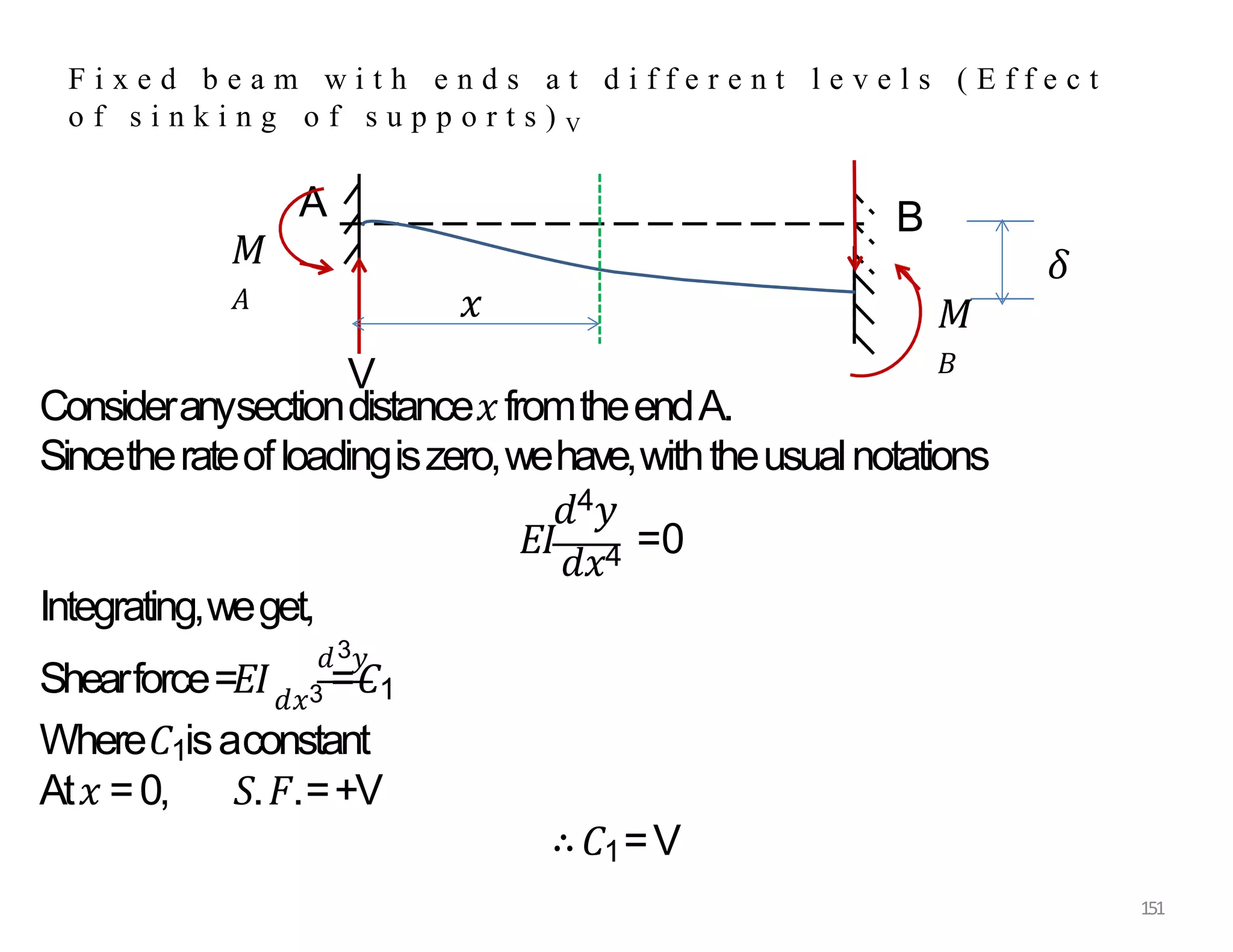
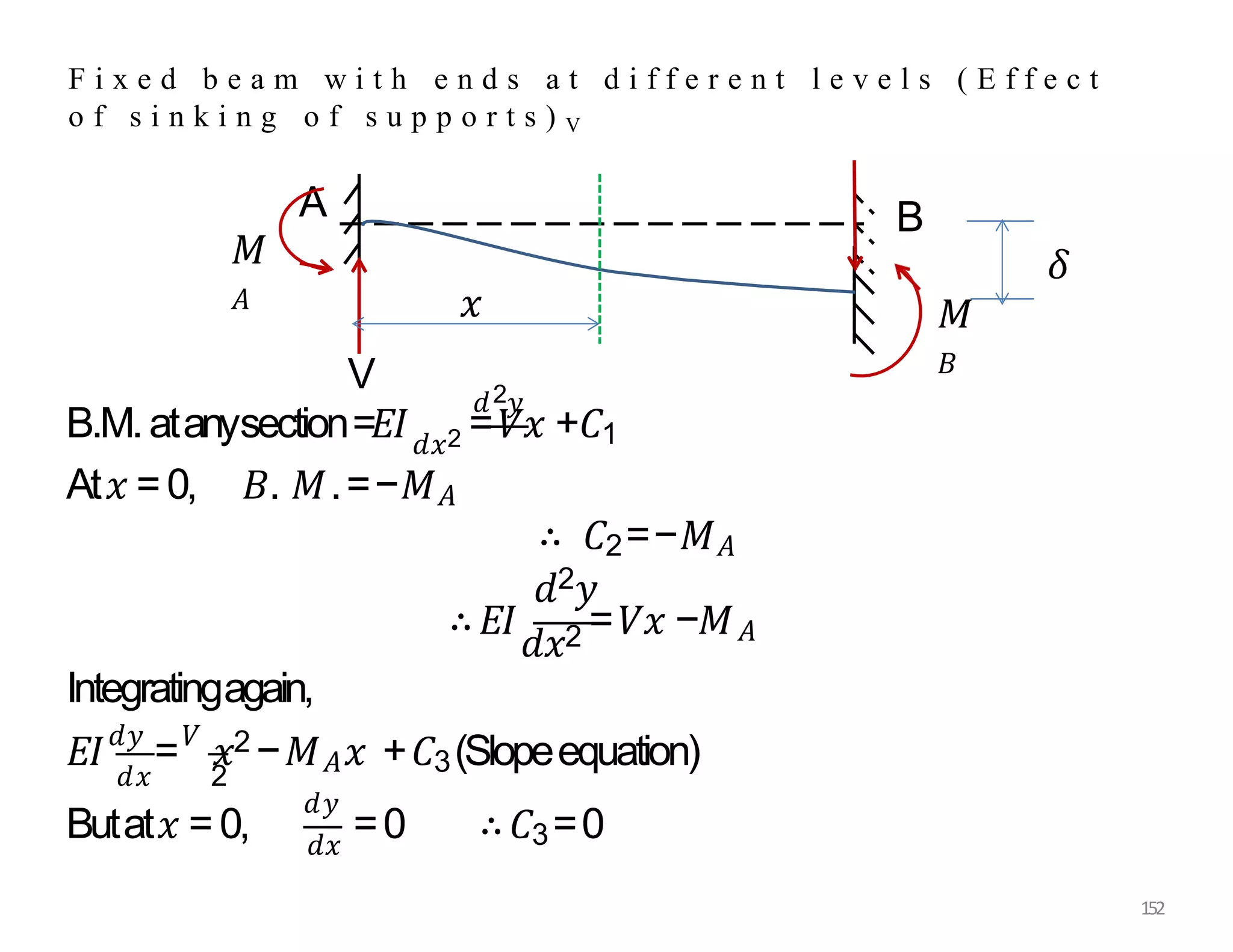
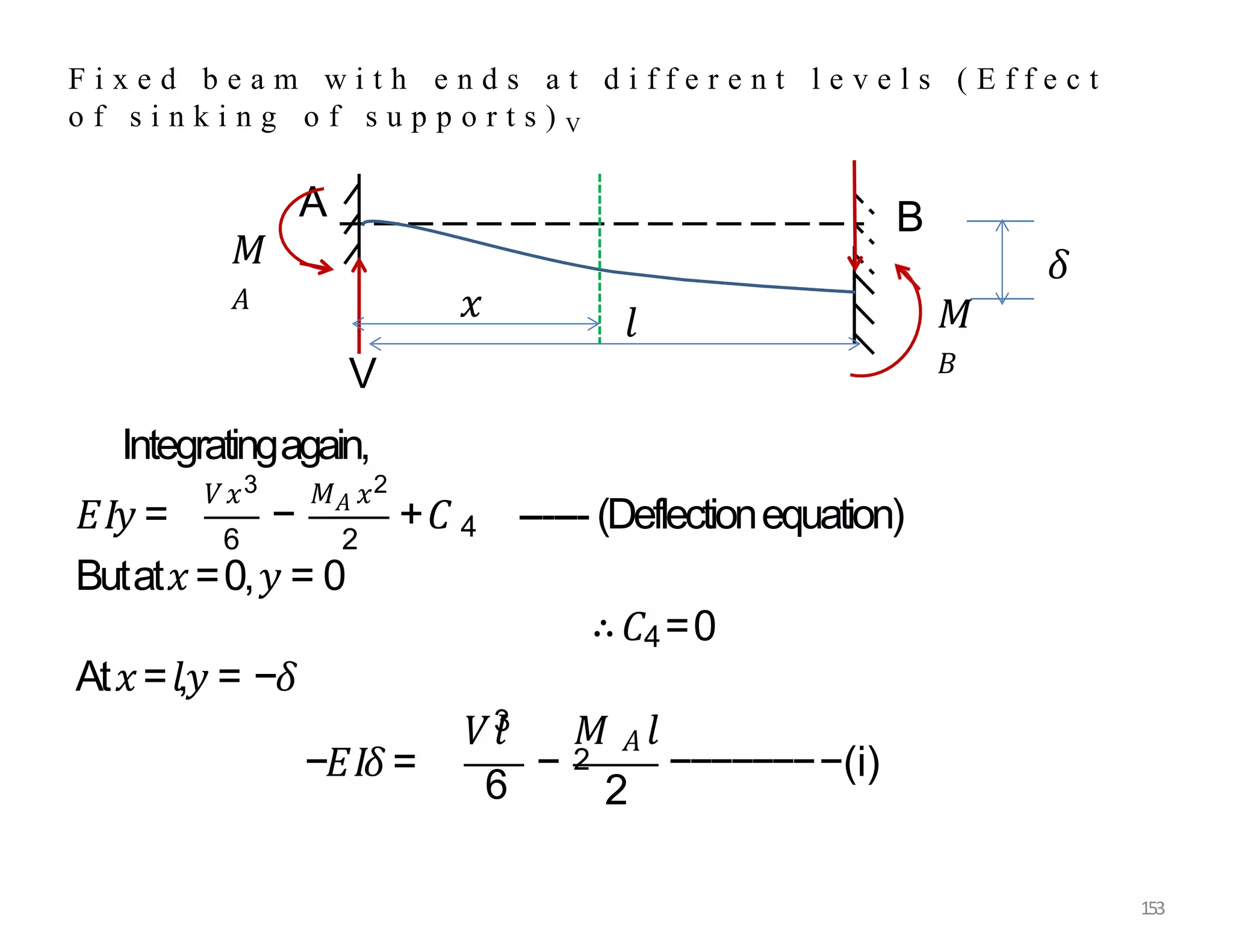
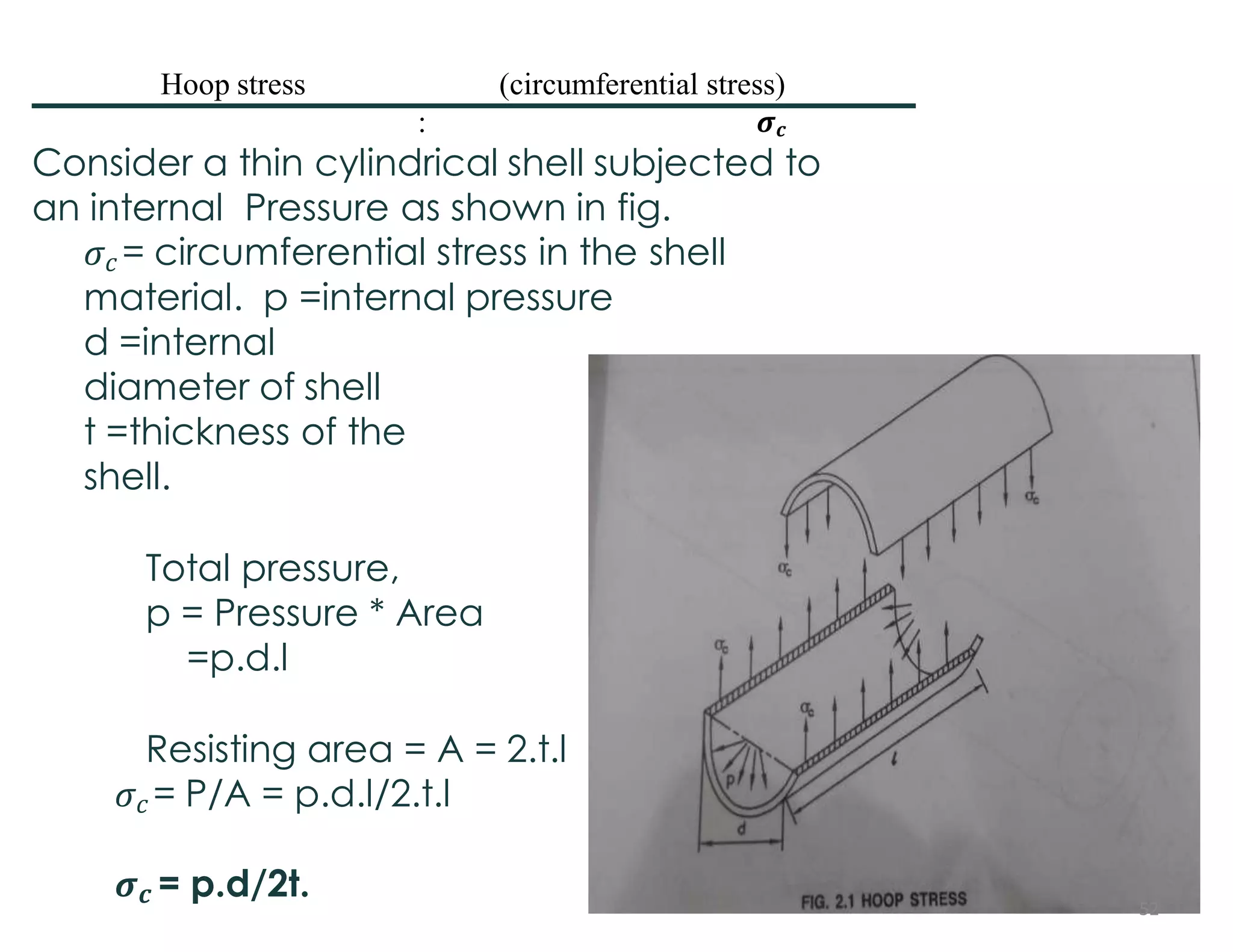
This document provides information about stresses and deflections in thin cylindrical shells. It discusses the following key points: - Thin cylindrical shells have constant hoop and longitudinal stresses over the thickness, while thick shells have variable stresses. - The hoop stress in a thin cylindrical shell subjected to internal pressure is equal to pressure times internal diameter divided by 2 times thickness. 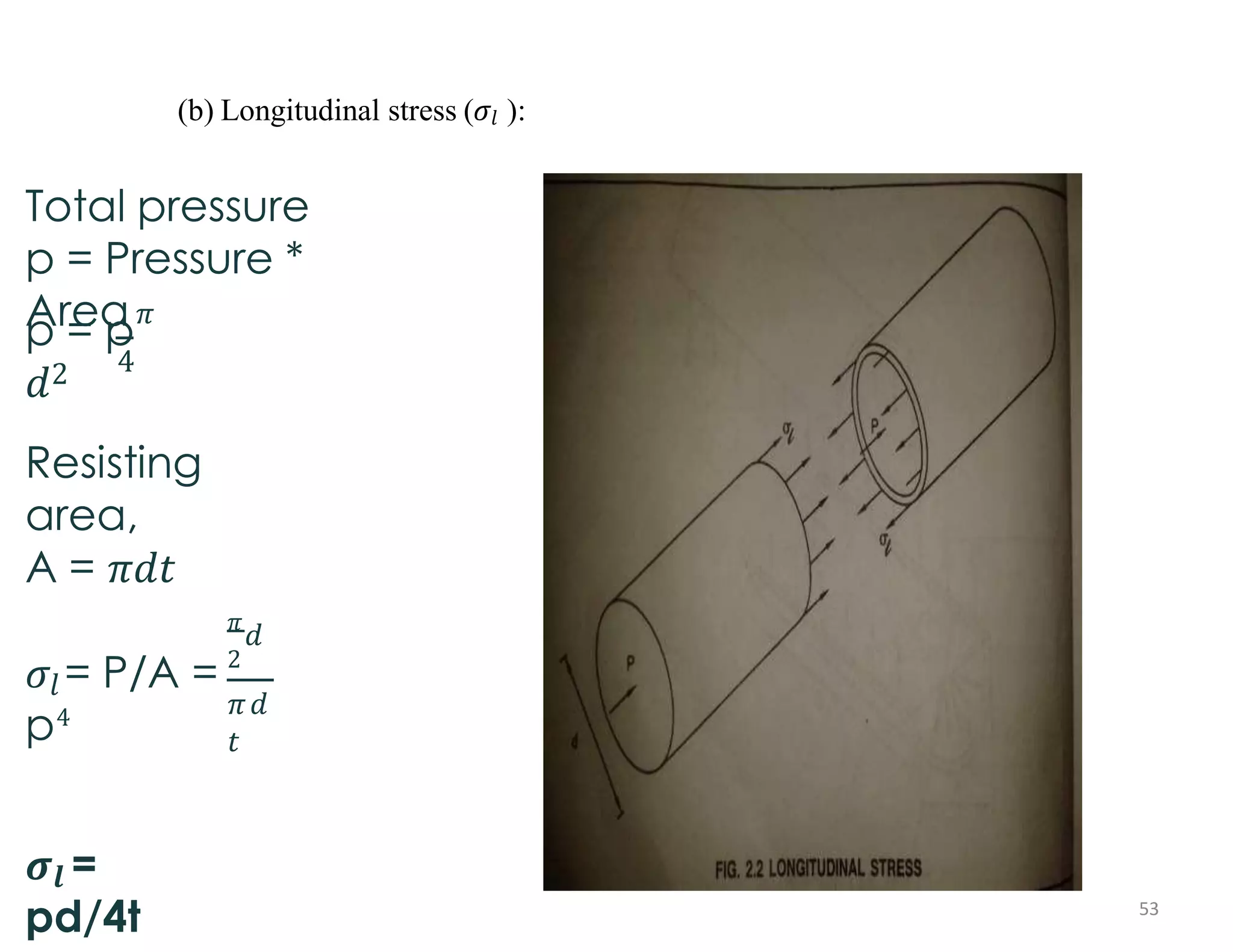- The longitudinal stress is equal to pressure times internal diameter divided by 4 times thickness. - The circumferential and longitudinal strains in a thin cylindrical shell can be calculated from the hoop and longitudinal stresses. This leads to changes in the internal diameter and length of the shell.

1. INSTITUTE OF AERONAUTICAL ENGINEERING
(AUTONOMOUS)
Dundigal – 500 043, Hyderabad
Regulation: R16 (AUTONOMOUS)
Course code: ACE004
STRENGTH OF MATERIALS – II
B.TECH IV SEMESTER
Prepared By
SURAJ BARAIK
Assistant Professor
1

2. Unit I
Deflectionin Beams
2

3. Deflection in Beams
• Topics Covered
 Review of shear force and bending moment diagram
 Bending stresses in beams
 Shear stresses in beams
 Deflection in beams
3

4. Beam Deflection
Recall: THE ENGINEERING BEAM THEORY

y

M E

I R
y
x
NA
A B
A’ B’
If deformation is small (i.e. slope is “flat”):
Moment-Curvature Equation
v (Deflection)
4

5. A
’
Alternatively: from Newton’s Curvature Equation
1 d2
y
 
R dx2
 
1 d
R dx
x
and  
y
(slope is “flat”)
y
x
R
y  f(x)
1 d2
y
 
R dx2


dx





dy

2
1
if 

R
1



d2
y



dx 


 2







1




dx





3


dy 

2


2
R
B’
y
5

6. From the Engineering Beam Theory:
M E

I R
1 M

R EI
d2
y

dx2
d2
y
 EI  M
dx2
Flexural
Stiffness
Bending
Moment
Curvature
6

7. Relationship
A B
C
B
A C
y
Deflection = y
Slope =
dy
dx
Shearing force = EI
d2
y
Bending moment = EI
dx2
d3
y
dx3
Rate of loading = EI
d4
y
dx4
7

8. Methods to find slope and deflection
 Double integration method
 Moment area method
 Macaulay’s method
8

9. Since,
d2
y
2

1 

dx 

EI



 

M Curvature
 
1

 

dy
dx 

EI


 
  M dx C1
Slope
1

 


EI

 y  
 
 1
  
M dx dx  C  dx  C2 Deflection
Where C1 and C2 are found using the boundary conditions.
Curvature Slope Deflection
R dy
dx
y
Double integration method
9

10. Double integrat io n met hod
Slope Deflection
B
L
L/2
A C
L/2
yc
Slope =
dy
dx
A B
2
WL
     
16EI
 
Deflection = yc
WL3
48EI
Slope Deflection
A C
yc
L
x w/Unit length
B Slope =
dy
dx
A B
2
WL
     
24EI
 
Deflection = yc
5 WL3
384 EI
Simple supported
W
Uniform distributed load
10

11. Macaulay’s method
 The procedure of finding slope and deflection for
simply supported beam with an eccentric load is very
laborious.
 Macaulay’s method helps to simplify the calculations
to find the deflection of beams subjected to point
loads.
11

12. 9- 11
Moment-Area Theorems
D
C xC
xD
M
 d   EI
dx
xC
xD
M
D  C   EI
dx
• Consider a beam subjected to arbitrary
loading,
d d2
y M
 
dx dx2
EI
• First Moment-Area Theorem:
area under BM diagram between
C and D.
dx
R d
CD  Rd  dx
12

13. 9- 12
Mo ment -Are a T heo rems
• Tangents to the elastic curve at P and P’
intercept a segment of length dt on the vertical
through C.
dt  xd  x
M
EI
dx
xC xC
xD xD
M 1 1
tC D   x
EI
dx 
EI
 xMdx 
EI
Ax

 A= total area of BM diagram between C & D
x = Distance of CG of BM diagram from C
• Second Moment-Area Theorem:
The tangential deviation of C with respect to
D is equal to the first moment with respectto
a vertical axis through C of the area under
the BM diagram between C and D.
13

14. Moment Area Method
14

15. An Exercise- Moment of Inertia – Comparison
Load
2x 8 beam
Maximum distance of 1 inch to
the centroid
I1
I2 > I1 , orientation 2 deflectsless
1
Maximum distance of
4inch to the centroid I2
Load 2
2x 8 beam
15

16. UNIT II
DEFLECTION BY ENERGY METHODS
16

17. Elastic Deflection
Castigliano’sMethod
Complementary
Energy U’
Incremental:
Deflection:
When a body is elastically deflected by any combination of loads, the
deflection at any point and in any direction is equal to the
partial derivative of strain energy (computed with all loads acting)
with respect to a load located at that point and acting
in that direction
Castiglino’s Theorem: ∆  U Q
17

18. Elastic Deflect io n
Castigliano’s M ethod
Energy and DeflectionEquations
Example: Axial Tension
Stored Elastic Energy:
Case 1 from Table 5.1:
gives: For varying E
and A:
18

19. Elastic Deflection
Castigliano’s Method
(1) Obtain expression for all components of energy
Table 5.3
(2) Take partial derivative to obtain deflection
∆  U Q
Castiglino’s Theorem:
Energy and DeflectionEquations
19

20. Elastic Deflection: Castigliano’s Method
Table 5.3
1. Energy: here it has two components:
first compute Energy, then Partial Derivative to get deflection
Here 2 types of loading: Bending and Shear magnitude @ x:
2. Partial Derivatives for deflection:
(23=8)*3*4 = 96
20

21. Table 5.3
Elastic Deflection: Castigliano’s Method
TWO METHODS
Differentiate after Integral Differentiate under Integral
21

22. Elastic Deflection: Castigliano’s Method
m
m
Transverse shear contributes only <5% to deflection
22

23. Elastic Deflection: Castigliano’s Method
Use of “Dummy Load” Q=0
•90° bend cantilever beam
•shear neglected
•Shear neglected => only 4 energy components:
1) BENDING portion a_b: Mab=Py
2) BENDING portion b_c: Mbc=Qx +Ph
3) TENSION portion a_b: Q
4) COMPRESSION portion b_c: P
(Tension and Compression mostly
negligible if torsion and bending
are present)
:
23

24. Elastic Deflection: Castigliano’s Method
•Eccentrically Load Column
•No Buckling
Redundant Support
500kg x 9.8m/s2
=4900 N
Guy wire
•Now Deflection known (=0) •Find necessary Tension Force F
•Hence partial derivative of total elastic energy with respect to F
must be zero
•Omit zero derivatives
- all energy terms above a
- compression term below a
•Only bending term is left: M= (4900 N)(1.2m)-Fy = 5880 Nm - Fy
finite value
(Nm)2 m Nm3 m3
(Nm)2 Nm
Nm3 m3
24

25. U  P/2
e
Energy Method
External Work
When a force F undergoes a
displacement dx in the same direction
as the force, the work done is
dUe  F dx
Ifthe total displacement is x the work
become
x
Ue   F dx
0
25

26. The work of a moment is defined by the product of the magnitude
of the moment M and the angle d then if the total
angle of

e
U  M/2

Ue   M d
0
rotation is the work become:
dUe M d

26

27. 27

28. 28

29. 29

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. 36

37. 37

38. 38

39. 39

40. 40

41. 41

42. 42

43. Maxwell–Betti Reciprocal theorem
Consider a simply supported beam of span L as
shown. Let this beam be loaded by two systems of
forces P1and P2 separately as shown in the figure. Let
u21 be the deflection below the load point P2 when only
load P1is acting.
Similarly let u12 be the deflection below load P1 , when
only load P2 is acting on the beam.
43

44. 44

45. The reciprocal theorem states that the work done by forces
acting through displacement of the second system is the same as
the work done by the second system of forces acting through the
displacements of the first system. Hence, according to
reciprocal theorem,
P1  u12  P2  u21
Now, u12 and u21 can be calculated using Castiglinao’s first
theorem. Substituting the values of u12 and u21 in equation we
get,
48EI 48EI
5P L3
5PL3
P 
2
 P 
1
45

46. Hence it is proved. This is also valid even when the first system of forces is
P1,P2,...., Pn and the second system of forces is given by Q1,Q2 ,....,Qn . Let
u1 , u2 ,...., un be the displacements caused by the forces P1, P2,...., Pnonly and
1, 2 ,...., n be the displacements due to system of forces Q1, Q2 ,...., Qn only
acting on the beam as shown in Fig
46

47. UNIT III
STRESSES IN CYLINDERS AND SPHERICAL SHELLS
47

48. THIN CYLINDER
48

49. Introduction
Cylindrical and spherical vessels are used in the
engineering field to store and transport fluids. Such vessels
are tanks ,boilers , compressed air receivers , pipe lines etc.
these vessels, when empty, are subjected to
atmospheric pressure internally as well as externally and the
resultant pressure on the walls of the shell is nil.
but whenever a vessel is subjected to an intenal
pressure
(due to air , water , steam etc.) its walls are subjected to
tensile stresses.
49

50. Thin cylindrical shell.
When t/d <= d/10 to d/15, it is called thin
cylindrical shell. t = thickness of the
shell
d =internal diameter of shell.
in thin cylindrical shells hoops stress and longitudinal stresses
are constant over the
Thickness and radial stresses are negligible.
When t/d > d/10 to d/15, it is called THICK cylindrical shell.
50

51. Stresses in thin cylindrical shells :
whenever, a thin cylindrical shell is subjected to
an internal pressure (p). Its Walls are subjected
to two types of tensile stresses.
(a) Hoop stress (circumferential stress)
(b) Longitudinal stress.
51

52. Consider a thin cylindrical shell subjected to
an internal Pressure as shown in fig.
𝜎𝑐 = circumferential stress in the shell
material. p =internal pressure
d =internal
diameter of shell
t =thickness of the
shell.
Total pressure,
p = Pressure * Area
=p.d.l
Resisting area = A = 2.t.l
𝜎𝑐 = P/A = p.d.l/2.t.l
𝝈𝒄 = p.d/2t.
Hoop stress (circumferential stress)
: 𝝈𝒄
52

53. (b) Longitudinal stress (𝜎𝑙 ):
Total pressure
p = Pressure *
Area
4
p = p𝜋
𝑑2
Resisting
area,
A = 𝜋𝑑𝑡
𝜎𝑙 = P/A =
p4
𝜋
𝑑
2
𝜋𝑑
𝑡
𝝈𝒍 =
pd/4t 53

54. Change in dimensions of a thin cylindrical shell due to internal
pressure:
1
𝜀
=
𝛿𝑑
𝜎
𝑐 𝜎
𝑙
= −
=
𝑝𝑑
−
𝑝
𝑑
𝑑 𝐸 𝑚𝐸 2𝑡𝐸
4𝑡𝑚𝐸
𝟏
𝜺𝟏 = 𝒑𝒅/𝟐𝒕𝑬(𝟏 −
𝟐𝒎
)
Longitudinal strain,
2
𝜀
=
=
𝛿𝑙
𝜎
𝑙
𝑙
𝐸
− 𝑐
𝑚𝐸 4
𝑡𝐸
𝜎
= 𝑝𝑑
−
𝑝
𝑑
2𝑡𝑚
𝐸
𝒑𝒅 𝟏
𝟏
𝜺𝟐 =
𝟐𝒕𝑬 𝟐
−
𝒎
Let, 𝛿𝑑=change in dia. Of
shell
𝜎𝑙=change in length
of shell
Circumferential strain,
54

55. Change in volume of a thin cylindrical shell due to internal pressure:
Volume of
shell,
V = 𝜋
∗ 𝑑2
∗𝑙
4
Final
volume,
4
V+𝛿𝑣 = 𝜋
𝑑 +
𝛿𝑑
2
∗
𝑙 +
𝛿𝑙
Change in
volume,
𝛿𝑣
=
𝑉 + 𝛿𝑣
− 𝑉
= [
𝜋
𝜋
4
4
2
2
𝑑 + 𝛿𝑑 ∗ (𝑙 + 𝛿𝑙)] − ∗
𝑑 ∗ 𝑙
2
2
𝜋
4
4
2
= [ 𝜋
(𝑑 + 2𝛿𝑑 ∗ 𝑑 + 𝛿𝑑 ) ∗ (𝑙 + 𝛿𝑙)]
− ∗ 𝑑
∗ 𝑙
=
𝜋 4
𝑑2𝑙 + 2𝛿𝑑 ∗ 𝑑 ∗ 𝑙 + 𝛿𝑑2 ∗ 𝑙 + 𝑑2 ∗ 𝛿𝑙 + 2𝛿𝑑 ∗ 𝑑 ∗ 𝛿𝑙
+ 𝛿𝑑2 ∗𝛿𝑙
𝜋
4
2
− 𝑑
∗ 𝑙
=
𝜋 4
𝑑2𝛿𝑙 + 2𝛿𝑑 ∗ 𝑑
∗ 𝑙
𝛿𝑣
=
𝜋
𝑉
4
4
𝑑2𝛿𝑙 + 2𝛿𝑑 ∗ 𝑑 ∗ 𝑙 /𝜋
∗
𝑑2 ∗ 𝑙
=𝛿𝑙
+ 2
𝛿𝑑
1
2
𝑑
𝑙
(𝜀 = 𝛿𝑑
, 𝜀 = 𝛿
𝑙
)
𝑙 𝑑
=𝜀2 + 2𝜀1
𝜹𝒗 =V(𝝐𝟐 + 𝟐
𝜺𝟏)
55

56. Thin spherical shells
Consider a thin spherical shell subjected to internal pressure p
as shown in fig.
p =internal pressure
d =internal
diameter of
shell t
=thickness of
the shell
𝜎 = stress in the shell material
Total force
P =
𝜋
∗ 𝑑2
∗𝑝
4
Resisting
section
=𝜋𝑑𝑡
Stress in the shell
𝜎 = 𝑇𝑜𝑡𝑎𝑙 force/resisting
section
4
=
𝜋
𝑑2𝑝/𝜋
𝑑𝑡 𝑝
𝑑
𝜎 =
56

57. Chenge in diameter and volume of a thin spherical shell due to internal pressure
Consider a thin spherical shell subjected to
internal pressure.
p =internal pressure
d =internal diameter of shell
t =thickness of the shell
𝜎 = stress in the shellmaterial
We know that for thin spherical shell
𝜎 =𝑝𝑑
4𝑡
Strain in any
direction
𝐸
𝑚𝐸
𝜖=
𝜎
−
=
𝜎 𝑝𝑑
−
𝑝
𝑑
4𝑡𝐸 4𝑡
𝑚𝐸 𝟏
𝒎
𝜺 = 𝒑𝒅/𝟒𝒕𝑬(𝟏
−
)
We know that,
strain,
∈
=
𝛿
𝑑
𝑑
𝑑
𝛿𝑑
=
𝟏
𝒎
𝒑𝒅/𝟒𝒕𝑬(𝟏
−
)
……(
1)
57

58. CLASSIFICATIONS OF SHELLS
58

59. • Shell is a type of building enclosures.
• Shells belong to the family of arches . They can be defined as curved or
angled structures capable of transmitting loads in more than two
directions to supports.
• A shell with one curved surface is known as a vault (single curvature ).
• A shell with doubly curved surface is known as a dome (double
curvature).
SHELLS
59

60. Classification of shells
• There are many different ways to classify shell structures but
two ways are common:
1. The material which the shell is made of: like reinforced
concrete, plywood or steel, because each one has different
properties that can determine the shape of the building
and therefore, these characteristics have to be considered
in the design.
2. The shell thickness: shells can be thick or thin.
60

61. Thin Concrete Shells
The thin concrete shell structures are a lightweight construction composed of a
relatively thin shell made of reinforced concrete, usually without the use of
internal supports giving an open unobstructed interior. The shells are most
commonly domes and flat plates, but may also take the form of ellipsoids or
cylindrical sections, or some combination thereof. Most concrete shell
structures are commercial and sports buildings or storage facilities.
There are two important factors in the development of the thin concrete
shell structures:
• The first factor is the shape which was was developed along the history of
these constructions. Some shapes were resistant and can be erected easily.
However, the designer’s incessant desire for more ambitious structures did
not stop and new shapes were designed.
• The second factor to be considered in the thin concrete shell structures is the
thickness, which is usually less than 10 centimeters. For example, the
thickness of the Hayden planetarium was 7.6 centimeters.
61

62. Types of Thin Concrete Shells
1. Barrels shells
The cylindrical thin shells, also called
barrels, should not be confused with the
vaults even with the huge similarity in
the shape of both structures, because
each of these structures has a different
structural behavior as well as different
requirements in the minimum thickness
and the shape.
62

63. • On one hand, the structural behavior of the vault is
based on connected parallel arches, which transmit
the same effort to the supports . Therefore, the
materials used in these structures have to be able to
resists compressions (e.g. stone) and the thickness is
usually higher. Furthermore, the shape of the vaults
must be as similar as possible to the arch in order to
achieve the optimum structural behavior.
• On the other hand, the structural behavior of the
barrels shell is that it carries load longitudinally as a
beam and transversally as an arch. and therefore, the
materials have to resist both compression and tension
stresses. This factor takes advantage of the bars of the
reinforced concrete, because these elements can be
placed where tension forces are needed and
therefore, the span to thickness Ratios can be
increased. Furthermore, the shape has fewer
requirements than the vaults and therefore, new
curves like the ellipse or the parabola can be used
improving the aesthetic quality of the structure.
63

64. 64

65. Types of Thin Concrete Shells
2. Folded plate
A thin-walled building structure of
the shell type.
Advantages of Folded Plate Roofs over Shell Roofs are:
(a) Movable form work can be employed.
(b) Form work required is relatively simpler.
(c) Design involves simpler calculations.
Disadvantages of Folded Plate Roofs over Shell Roofs are:
(a) Folded plate consumes more material than shells.
(b) Form work may be removed after 7 days whereas in
case of shells it can be little earlier.
65

66. Folded plate types
66

67. Folded Plates system
67

68. 68

69. 69

70. Folded-Plate Hut in Osaka
70

71. Folded Plates Library
71

72. 72

73. 73

74. 74

75. Types of Thin Concrete Shells
3. Hyperbolic Paraboloid (Hypar)
A Hypar is a surface curved in two
directions that can be designed as a shell
or warped lattice.
A hypar is triangular, rectangular or
rhomboidal in plan, with corners raised to
the elevation desired for use and/or
appearance. The edges of Hypars are
typically restrained by stiff hollow beams
that collect & transfer roof loads to the
foundations. Rhomboi
d
75

76. 76

77. 77

78. Types of shells
4. Various Double Curvature
78

79. 79

80. Types of Thin Concrete Shells
5. Dome
A rounded roof, with a circular base,
shaped like an arch in all directions..
First used in much of the Middle
East and North Africa whence it
spread to other parts of the Islamic
world, because of its distinctive
form the dome has, like the
minaret, become a symbol of
Islamic architecture.
Dome has double curvature and the
resulting structure is much stiffer
and stronger than a single curved
surface, such as a barrel shell.
80

81. 81

82. 82

83. 83

84. 84

85. Types of Thin Concrete Shells
6. Translation Shells
A translation shell is a dome set on
four arches. The shape is different
from a spherical dome and is
generated by a vertical circle moving
on another circle. All vertical slices
have the same radius. It is easier to
form than a spherical dome.
85

86. • Advantages of Concrete Shells:
The curved shapes often used for concrete shells are
naturally strong structures.
Shell allowing wide areas to be spanned without the use
of internal supports, giving an open, unobstructed
interior.
The use of concrete as a building material reduces both
materials cost and the construction cost.
As concrete is relatively inexpensive and easily cast into
compound curves.
• Disadvantages of Concrete Shells
Since concrete is porous material, concrete domes often
have issues with sealing. If not treated, rainwater can
seep through the roof and leak into the interior of the
building. On the other hand, the seamless construction
of concrete domes prevents air from escaping, and can
lead to buildup of condensation on the inside of the
shell. Shingling or sealants are common solutions to the
problem of exterior moisture, and ventilation can
address condensation.
86

87. UNITIV
INDETERMINATE BEAMS:
PROPPED CANTILEVER AND FIXED
BEAMS
87

88. Contents:
• Concept of Analysis -Propped cantilever and
fixed beams-fixed end moments and
reactions
• Theorem of three moments – analysis of
continuous beams – shear force and
bending moment diagrams.
88

89. 89
Indeterminate beams
• Staticallydeterminatebeams:
– Cantilever beams
– Simple supported beams
– Overhanging beams
• Statically indeterminate beams:
– Propped cantilever beams
– Fixed beams
– Continuous beams

90. • Propped cantilever
Beams:
Indeterminate beams
Degree of static indeterminacy=
N0. of unknown reactions – static
equations=3-2 = 1
90

91. • Fixed beam:
A fixed beam is a beam whose end supports are such
that the end slopes remain zero (or unaltered) and is
also called a built-in or encaster beam.
Indeterminate beams
Degree of static indeterminacy=
N0. of unknown reactions – static
equations=4-2 =2
91

92. Degreeof staticindeterminacy=
N0.of unknownreactions– staticequations=5-2=3
Continuousbeam:Continuousbeamsare very commonin the structural
design.For the analysis,theoremof threemomentsis useful.
Abeamwith morethan 2 supportsprovidedis knownas continuous
beam.
Degreeof staticindeterminacy=
N0.of unknownreactions– staticequations=3-2=1
92

93. •B.M. diagram for a fixed
beam : Figure shows a fixed
beam AB carrying an external
load system. Let VA and VB be
the vertical reactions at the
supports A and B.
LetMAand MB be the fixed end
Moments.
𝑀
𝐵
𝑀
𝐴
𝑉𝐴
𝑉𝐵
𝑊
1
𝑊
2
𝑊
1
𝑊
2
93

94. vb
Thebeammay be analyzedin the followingstages.
(i) Letus firstconsiderthe beamas Simplysupported.
Letva andvb be the verticalreactionsat the supportsAand B.
Figure(ib) showsthe bendingmomentdiagramfor this condition.
At anysectionthe bendingmomentMx is a saggingmoment.
𝑊1 𝑊2
va
Fixed Beams
(ib)FreeB.M.D.
94
(ia)Freelysupportedcondition
𝑀𝑥

95. • (ii)NowletusconsidertheeffectofendcouplesMAandMB alone.
Letv be the reactionat each
enddue to this condition.
Suppose𝑀𝐵 > 𝑀𝐴.
Then𝑉 =𝑀𝐵−𝑀𝐴
.
𝐿
If 𝑀𝐵 >𝑀𝐴 thereactionV is
upwardsat B and downwardsatA.
Fig Showsthe bendingmoment
diagramfor this condition.
At anysectionthe bendingmomentMx’ is hoggingmoment.
𝑀
𝐴
𝑀
𝐵
v
v
(iia)Effectofendcouples
(iib)FixedB.M.D.
𝑀
𝑥
′
95

96. • Nowthe finalbendingmoment
diagramcanbe drawnby
combiningthe above two B.M.
diagramsas shownin Fig.(iiib)
Nowthe finalreactionVA=va- v
andVB = vb + v
Theactualbendingmomentat any
𝑑2𝑦
sectionX, distance𝑥 fromthe endAis given by,
𝐸𝐼
𝑑𝑥2= 𝑀𝑥 − 𝑀𝑥′
𝑀
𝐴
𝑉𝐴
𝑀𝐵
𝑉
𝐵
𝑊1 𝑊2
(iiib)ResultantB.M.D.
+
96
-
-

97. Fixed B eams
𝑀
𝐵
𝑀
𝐴
𝑉𝐴
𝑉
𝐵
𝑊
1
𝑊
2
𝑉𝑎 𝑉𝑏
(ia)Freelysupportedcondition
𝑀
𝐴
𝑀
𝐵
𝑉 𝑉
(iiia)Fixedbeam
(iia)Effectofendcouples
𝑊1 𝑊2
𝑀
𝑥
𝑀
𝑥′
+
-
-
(iib)FixedB.M.D.
(iiib)ResultantB.M.D.
(ib)FreeB.M.D.
97

98. • Integrating,weget,
• 𝐸𝐼
𝑑𝑦
𝑑𝑥
𝑙
0
= 𝑥
𝑀 𝑑𝑥− 𝑥
′
𝑀 𝑑
𝑥
𝑙
0
𝑙
0
• Butatx=0,𝑑𝑦
=0
𝑑𝑥
𝑑𝑦
andat𝑥=𝑙,𝑑𝑥
= 0
𝑙
Further0 𝑀𝑥𝑑𝑥 =areaoftheFreeBMD=𝑎
𝑥
𝑙
𝑀 ′ 𝑑𝑥 =areaofthefixed B.M.D=𝑎′
0
Substitutingintheaboveequation,weget,
0=𝑎 − 𝑎′
∴𝑎 = 𝑎′
𝑑2𝑦
𝐸𝐼
𝑑𝑥2 =𝑀𝑥 −𝑀𝑥′
98

99. • Integratingweget,
•
2
𝑑𝑥2
𝐸𝐼
𝑥 = 𝑥
𝑀 𝑥𝑑𝑥 − 𝑥
′
𝑀 𝑥𝑑
𝑥
𝑙
0
𝑙
0
𝑙 𝑑 𝑦
0
𝑑𝑥 0
• ∴ 𝐸𝐼 𝑥𝑑𝑦
−𝑦 𝑙
=a𝑥-a’𝑥′
• Where𝑥=distanceofthecentroidofthefreeB.M.D.fromA. and𝑥′=
distanceofthecentroidofthefixedB.M.D.fromA.
Fixed Beams
𝑑2𝑦
𝑎 = 𝑎′
∴AreaofthefreeB.M.D.=AreaofthefixedB.M.D.
Againconsidertherelation,
𝐸𝐼
𝑑𝑥2 =𝑀𝑥 −𝑀𝑥′
𝑑2𝑦
𝑑𝑥2 𝑥 𝑥
99
′
𝐸𝐼𝑥 =𝑀 𝑥−𝑀 𝑥
𝑀𝑢𝑙𝑡𝑦𝑖𝑛𝑔𝑏𝑦 𝑥𝑤𝑒𝑔𝑒𝑡,

100. 𝑑𝑥
• Furtherat x=0, y=0 and 𝑑𝑦
= 0
or
100
• andat x=l, y=0 and 𝑑𝑦
= 0.
𝑑𝑥
• Substitutingin the above relation,we have
0 = 𝑎𝑥-𝑎′𝑥′
𝑎𝑥=𝑎′𝑥′
𝑥 =𝑥
∴The distanceof the centroidof the freeB.M.D . FromA=The
distanceof the centroidof the fixed B.M.D. fromA.
∴ 𝑎 = 𝑎′
𝑥 = 𝑥
Fixed Beams

101. Fixed Beams
𝑀𝐵
𝑀𝐴
𝑉𝐴 𝑉
𝐵
𝑊
1
𝑊
2
𝑉𝑎 𝑉𝑏
(ia)Freelysupportedcondition
𝑀𝐴 𝑀𝐵
𝑉 𝑉
(iiia)Fixed beam
(iia)Effectof end couples
𝑊1 𝑊2
𝑀𝑥
𝑀𝑥′
+
-
-
(iib)Fixed B.M.D.
(iiib)ResultantB.M.D.
(ib)FreeB.M.D.
101

102. Fixed beam problems
• Findthe fixed endmomentsof a fixed beamsubjectedto a
pointloadat the center.
W
l/2
A
102
B
l/2

103. • 𝐴′ =𝐴
𝑊 𝑙
𝑀 =
8
=𝑀𝐴 = 𝑀𝐵
𝑙
/2
Fixed beam problems
W
A B
𝑊 𝑙
4
FreeBMD
𝑙
/2
M
M
+
-
𝑀 ×𝑙
=
1
×𝑙
×
𝑊𝑙
2 4
+
- -
FixedBMD
𝑊 𝑙
4
ResultantBMD
103

104. • Findthefixedendmomentsofafixedbeamsubjectedto a
eccentricpointloadW.
W
a
A B
b
𝑙
104
Fixed b eam p ro b lems

105. Fixed beam problems
• 𝐴′ =𝐴
19
• 𝑥′ =𝑥
𝑀𝐴 +2𝑀
𝐵
𝑀𝐴 +𝑀
𝐵
×
3
=
𝑙 𝑙
+𝑎
3
𝐵
𝑀 =𝑀 ×
𝑎
𝑙
−𝑎
𝐴
𝑎
𝑀𝐵 =
𝑏
−−−(2)
𝑎
W
B
𝑙
𝑏
+
𝑀𝐴 +𝑀
𝐵
1
×𝑙
=
2
×𝑙
×
A
𝑊𝑎𝑏
2 𝑙
𝑙
𝑊𝑎𝑏
FixedBMD
𝑀
𝐴 𝑀
𝐵
Free-BMD
-
𝐴
𝐵
𝑙
𝑀 +𝑀 =
𝑊𝑎𝑏
−−−−(1)
105

106. 𝑎
𝑎
W
A B
𝑏
𝐴
𝐵
𝑙
𝑀 +𝑀 =
𝑊𝑎𝑏
−−−−(1)
+
𝑊 𝑎𝑏
2
𝑙
2 𝑊 𝑏
𝑎
2
𝑙
2
𝑙
𝑊 𝑎
𝑏
𝑙
ResultantBMD
- -
𝑀𝐵 =𝑀𝐴 ×
𝑏
−−−(2)
Bysubstituting(2)in(1),
𝑀𝐴 =
𝑊 𝑎 𝑏
2
𝑙2
From(2),
𝑀𝐵 =
𝑊 𝑏𝑎
2
𝑙2
106
Fixed beam problems

107. Clapeyron’s theorem of three moments
• AsshowninaboveFigure,ABandBCareanytwosuccessive spansof
acontinuousbeamsubjectedtoanexternal loading.
• If theextremeendsAandCfixedsupports,thesupport moments𝑀𝐴,
𝑀𝐵and 𝑀𝐶 atthesupportsA,BandCaregiven bytherelation,
𝑀 𝐴 𝑙
1 +2𝑀 𝐵 𝑙
1 +𝑙
2 +𝑀 𝐶 𝑙
2 =
6𝑎1𝑥1
+
6𝑎2𝑥2
𝑙
1 𝑙
2
A C
𝑙
1 𝑙
2
𝑀
𝐴
𝑀
𝐶
B𝑀
𝐵
107

108. Clapeyro n’s theore m of three mome nt s (contd…)
𝑀 𝐴 𝑙
1 +2𝑀 𝐵 𝑙
1 +𝑙
2 +𝑀 𝐶 𝑙
2 =
6𝑎1𝑥1
+
6𝑎2𝑥2
𝑙
1 𝑙
2
• Where,
• 𝑎1 =areaofthefreeB.M.diagramforthespanAB.
• 𝑎2 =areaofthefreeB.M.diagramforthespanBC.
• 𝑥1
=CentroidaldistanceoffreeB.M.DonABfromA.
• 𝑥2=CentroidaldistanceoffreeB.M.DonBCfromC.
108

109. 𝑑𝑥 𝑀
𝑥
+
𝑥1
𝑥
+
𝑥2
A B C
(a)
(b)
+
ve +
ve
𝑀
𝐴
𝑀𝐶 (d)
𝑑𝑥
𝑥
𝑀
𝑥’
𝑥2
′
𝑥1
′
𝑀
𝐴
𝑀
𝐶
(c)
+
+
FreeB.M.D
𝑀𝐵
FixedB.M.D
𝑀𝐵
-ve
Clapeyro n’s theore m of three mome nt s (contd…)
𝑙
1
109
𝑙
2

110. C l a p e y r o n ’ s t h e o r e m o f t h r e e m o m e n t s ( c o n t d … )
𝑑𝑥 𝑀
𝑥
+
𝑥1
𝑥
+
𝑥2
A B C
𝑑𝑥
𝑥
𝑀
𝑥’
𝑥2
′
𝑥1
′
𝑀
𝐴
110
𝑀
𝐶
-
-
FreeB.M.D
𝑀𝐵
FixedB.M.D
(a)Thegivenbeam
(b)FreeB.M.D.
(c)FixedB.M.D.

111. C l a p e y r o n ’ s t h e o r e m o f t h r e e m o m e n t s ( c o n t d … )
• Considerthe spanAB:
• Letat anysectioninAB distant𝑥 fromAthe free and fixed
bendingmomentsbe 𝑀𝑥 and𝑀𝑥
′ respectively.
• Hencethe net bendingmomentat the sectionis given by
𝑑2𝑦
𝐸𝐼
𝑑𝑥2= 𝑀𝑥 −𝑀𝑥
′
• Multiplyingby 𝑥, we get
𝐸𝐼𝑥
𝑑2𝑦
𝑑𝑥2 𝑥 𝑥
111
′
= 𝑀 𝑥 −𝑀 𝑥

112. • 𝐸𝐼
𝑥
2
𝑑 𝑦
𝑑𝑥2 𝑥 𝑥
′
= 𝑀 𝑥−𝑀 𝑥
𝑑2𝑦
𝑙
1 𝑙
1
• Integratingfrom𝑥=0𝑡𝑜𝑥=𝑙1,we get,
𝐸𝐼 𝑥
𝑑𝑥2 = 𝑀𝑥𝑥 𝑑𝑥 −𝑀𝑥
′𝑥 𝑑𝑥
𝑙
1
0 0
0
𝑑𝑦
𝐸𝐼 𝑥.
𝑑𝑥
−𝑦
112
0
𝑙
1
𝑙1 𝑙1
= 𝑀𝑥𝑥 𝑑𝑥 −𝑀𝑥
′𝑥 𝑑𝑥
0 0
−−−(1)
Clapeyro n’s theore m of three mome nt s (contd…)

113. • Butit maybesuchthat
At𝑥 =0, deflection𝑦 =0
𝑑𝑥
• At𝑥=𝑙1,𝑦 =0;𝑎𝑛𝑑 𝑠𝑙𝑜𝑝𝑒𝑎𝑡𝐵 𝑓𝑜𝑟𝐴𝐵, 𝑑𝑦
=𝜃𝐵𝐴
• 𝑥
𝑙1
0
𝑀 𝑥𝑑𝑥 =𝑎 𝑥
1 1 =MomentofthefreeB.M.D.onABaboutA.
•
𝑙1
0 𝑥 1
′
1
′
′
𝑀 𝑥𝑑𝑥 =𝑎 𝑥 =MomentofthefixedB.M.D.onABaboutA.
Clapeyro n’s theore m of three mome nt s (contd…)
A B C
𝑙
1 𝑙
2
𝑥
113

114. 𝑑𝑦
𝐸𝐼 𝑥.
𝑑𝑥
−𝑦
0
𝑙
1
𝑙1 𝑙1
= 𝑀𝑥𝑥 𝑑𝑥 −𝑀𝑥
′𝑥 𝑑𝑥
0 0
−−(1)
• Thereforetheequation(1)issimplifiedas,
1
𝐸𝐼 𝑙1𝜃𝐵𝐴 −0 =𝑎1𝑥1 −𝑎′𝑥1
′.
1
But𝑎′ =areaofthefixedB.M.D.onAB=
𝑀 𝐴 +
𝑀 𝐵
2
𝑙
1
𝑥1
′ =CentroidofthefixedB.M.D.fromA=
𝑀 𝐴 +2𝑀 𝐵 𝑙
1
𝑀 𝐴 +𝑀 𝐵 3
Clapeyro n’s theore m of three mome nt s (contd…)
114

115. • Therefore,
Clapeyro n’s theore m of three mome nt s (contd…)
𝟏
𝒂′ 𝒙𝟏
′ =
(𝑴𝑨 +𝑴𝑩 ) 𝑴 𝑨 +𝟐𝑴
𝑩 𝒍𝟏×
𝒍
𝟏
𝟐 𝑴 𝑨 +𝑴 𝑩
𝟑
=(𝑴𝑨 +𝟐𝑴𝑩 )
𝟏
𝒍
𝟐
𝟔
𝑬𝑰𝒍𝟏𝜽𝑩𝑨 = 𝒂𝟏
𝒙𝟏 −(𝑴𝑨 +𝟐𝑴𝑩 ) 𝟏
𝒍
𝟐
𝟔
𝒍
𝟏
𝟔𝑬𝑰𝜽𝑩𝑨 = 𝟔𝒂𝟏𝒙𝟏
−(𝑴𝑨 +𝟐𝑴𝑩)𝒍𝟏 −−−−(𝟐)
SimilarlybyconsideringthespanBCandtakingCasoriginit can be
shownthat,
𝟔𝑬𝑰𝜽𝑩𝑪 = 𝟔𝒂𝟐 𝒙
𝟐
−(𝑴𝑪 +𝟐𝑴𝑩)𝒍𝟐 −−−−(𝟑)
𝒍𝟐
𝜃𝐵𝐶 =slopefor spanCBatB
115

116. Clapeyro n’s theore m of three mome nt s (contd…)
• But𝜃𝐵𝐴 = −𝜃𝐵𝐶 asthedirectionof𝑥fromAforthespanAB,
andfromCforthespanCBareinoppositedirection.
• Andhence,𝜃𝐵𝐴+𝜃𝐵𝐶 =0
𝟔𝑬𝑰𝜽𝑩𝑨 = 𝟔𝒂𝟏𝒙𝟏
−(𝑴𝑨 +𝟐𝑴𝑩)𝒍𝟏 −−−−(𝟐)
𝒍𝟏
𝒍
𝟐
𝟔𝑬𝑰𝜽𝑩𝑪 = 𝟔𝒂𝟐𝒙 𝟐
−(𝑴𝑪 +𝟐𝑴𝑩)𝒍𝟐 −−−−(𝟑)
• Addingequations(2)and(3),weget
𝑬𝑰𝜽𝑩𝑨 +𝟔𝑬𝑰𝜽𝑩𝑪 =
𝟔𝒂𝟏𝒙𝟏
+
𝟔𝒂𝟐𝒙𝟐
−(𝑴𝑨 +𝟐𝑴𝑩)𝒍𝟏 −(𝑴𝑪 +𝟐𝑴𝑩)𝒍𝟐
𝒍𝟏 𝒍𝟐
𝟔𝑬𝑰(𝜽𝑩𝑨 +𝜽𝑩𝑪) =
𝒍
𝟏
𝟏 𝟏 𝟐 𝟐
𝟔𝒂 𝒙 𝟔𝒂 𝒙
𝒍
𝟐
𝑨 𝟏 𝑩 𝟏 𝟐 𝑪
𝟐
116
+ − 𝑴 𝒍 +𝟐 𝑴 (𝒍 +𝒍) +𝑴 𝒍

117. Clap eyro n ’s theo re m o f three mo me nt s (co ntd …)
𝟎 =
𝟔𝒂𝟏𝒙
𝟏
𝒍𝟏
+
𝟔𝒂𝟐𝒙
𝟐
𝒍𝟐
−𝑴𝑨𝒍𝟏 +𝟐𝑴𝑩(𝒍𝟏 +𝒍𝟐) +𝑴𝑪𝒍𝟐
𝑴𝑨𝒍𝟏 +𝟐𝑴𝑩(𝒍𝟏 +𝒍𝟐) +𝑴𝑪𝒍𝟐 =
𝟔𝒂 𝒙
𝟏 𝟏
𝒍𝟏
+
𝟔𝒂 𝒙
𝟐 𝟐
𝒍𝟐
117

118. 118
P roblems
• Acontinuous beam of three equal span is simply supported over
two supports. It is loaded with a uniformly distributed load of
w/unit length, over the two adjacent spans only. Using the
theorem of three moments, find the support moments and
sketchthe bendingmomentdiagram.AssumeEI constant.

119. P roblems
• Solution:
• Thetheoremof three
momentsequationfortwospansis,
𝑀 𝐴 (𝑙
1) +2𝑀 𝐵 𝑙
1 +𝑙
2 +𝑀 𝐶 𝑙2 =
6𝑎1𝑥1
+
6𝑎2𝑥2
𝑙1 𝑙2
ApplythetheoremofthreemomentequationforspansABandBCis,
𝑀 𝐴 𝑙 +2𝑀 𝐵 𝑙
+𝑙 +𝑀 𝐶 𝑙
=
6𝑎1𝑥1
+
6𝑎2𝑥2
𝑙
1 𝑙
2
𝑙
A
w/ unitlength
B C D
𝑙
𝑤 𝑙
2
8
𝑙
𝑤 𝑙
2
8
FreeB.M.D.
119

120. P roblems
1
• Solution:
• 𝑎 =2
×𝑙
×𝑤𝑙2
3 8
1
12
= 𝑤 𝑙
3
• 𝑥1= 𝑙
2
2
• 𝑎2 =3
×𝑙
×
𝑤 𝑙
2
8
• 𝑥2= 𝑙
2
𝑙
6×
1
𝑤𝑙3×
𝑙
6×
1
𝑤𝑙3×
𝑙
= 12 2
+ 12
2 𝑙
𝐵 𝐶 2
• 4𝑀 +𝑀 =𝑤𝑙2
−−−− −(1)
𝑙
A
w/ unitlength
B C D
𝑙
𝑤 𝑙
2
8
𝑙
𝑤 𝑙
2
8
FreeB.M.D.
0
• 𝑀 𝐴 𝑙 +2𝑀 𝐵 𝑙
+𝑙 +𝑀 𝐶 𝑙
120

121. • Solution:
• Thetheoremof three
momentsequationfortwospansis,
𝑀 𝐴 (𝑙
1) +2𝑀 𝐵 𝑙
1 +𝑙
2 +𝑀 𝐶 𝑙2 =
6𝑎1𝑥1
+
6𝑎2𝑥2
𝑙1 𝑙2
ApplythetheoremofthreemomentequationforspansBCandCDis,
𝑀 𝐵 𝑙 +2𝑀 𝐶 𝑙
+𝑙 +𝑀 𝐷 𝑙
𝑙
1
=
6𝑎1𝑥1
+0
𝑙
A
w/ unitlength
B C D
𝑙
𝑤 𝑙
2
8
𝑙
𝑤 𝑙
2
8
FreeB.M.D.
121

122. P roblems
1
• Solution:
• 𝑎 =2
×𝑙
×𝑤𝑙2
3 8
1
12
= 𝑤 𝑙
3
• 𝑥1= 𝑙
2
6×
1
𝑤𝑙3×
𝑙
𝑙
= 12 2
+0
𝐵 𝐶 4
• 𝑀 +4𝑀 =𝑤𝑙2
−−−−−(2)
𝑙
A
w/ unitlength
B C D
𝑙
𝑤 𝑙
2
8
𝑙
𝑤 𝑙
2
8
FreeB.M.D.
0
• 𝑀 𝐵 𝑙 +2𝑀 𝐶 𝑙
+𝑙 +𝑀 𝐷 𝑙
122

123. P ro b lems
• 4𝑀𝐵 +16𝑀𝐶 =w𝑙2−−−−−(2) ×4
4𝑀𝐵 +𝑀𝐶 =
𝑤 𝑙
2
2
−−−−−(1)
𝑤 𝑙
2
𝑀 𝐶 =
30
15𝑀𝐶 =
𝑤 𝑙
2
2
−−−−− 2 ×4−(1)
𝑤 𝑙
2
Substitute𝑀𝐶 = 30
inequation(2),
𝑀 𝐵 +4×
30
=
𝑤 𝑙
2 𝑤 𝑙
2
4
𝑀𝐵 =
7𝑤 𝑙
2
60
123

124. 124
Fixed beam P roblems
• AfixedbeamABofspan6mcarriesuniformlyvaryingloadof intensity
zeroatAand20kN/matB.Findthefixedend momentsanddrawthe
B.M.andS.F
.diagramsforthe beam.

125. P roblems
ConsideranysectionXXdistant𝑥fromtheendA,theintensityof
loadingatXX= =
𝑤 𝑥 20𝑥
𝐿 6
Hencetheloadactingforanelementaldistance𝑑𝑥 =
20𝑥
6
𝑑𝑥
Duetothiselementalloadthefixedmomentsareasfollows:
𝑑𝑀𝑎 =
Wa𝑏2
𝐿2 (Formula is derivedfromfirstprinciples)
= 6
20𝑥𝑑𝑥 ×𝑥× 6−𝑥 2
62
=
20𝑥2 6−𝑥 2𝑑𝑥
63
A B
20kN/m
20×𝑥
6
𝑥 X
6m
X
𝑑𝑥
125

126. P roblems
and
𝑑𝑀𝑏 =
W𝑏𝑎2
𝐿2 Formulais derivedfrombasicprinciples
= 6
20𝑥
𝑑𝑥× 6−𝑥 ×𝑥2
62 =
20𝑥3 6−𝑥 𝑑𝑥
63
𝑀𝐴 = 𝑑𝑀𝑎
T
akingfixingmomentatA,
𝑙
0
216
6
0
=
20
𝑥2 6−𝑥 2𝑑𝑥
A B
20kN/m
20×𝑥
6
𝑥 X
6m
X
𝑑𝑥
126

127. Problems
𝐴
216
𝑀 =
20
𝑥2 36+𝑥2 −12𝑥 𝑑𝑥
6
0
20 36𝑥3
=
216 3
𝑥5
+
5
−
12𝑥4
4
0
6
20 36×63 65
+
5
−
12×64
4
=
216 3
∴𝑀𝐴 =24kNm
127

128. P roblems
𝐵
𝑀 = 𝑑𝑀 𝐵
𝑙
0
63
=
20
𝑥3 6−𝑥 𝑑𝑥
6
0
20
=
216
𝑥4 𝑥5
4
×6−
5
0
6
20 64×6
=
216 4
65
−
5
∴𝑀𝐵 =36kNm
128

129. P roblems
A
B
20kN/m
20×𝑥
6
𝑥 X
6m
X
𝑑𝑥
FreeBMD:
𝑀𝑚𝑎 𝑥 =
𝑤 𝑙
2
=
20×62
9 3 9 3
=46.18kNm(Cubicparaboliccurve)
Willoccurat6 3mfromleftendA.
46.18kNm
+
6 3
FreeBMD
FixedBMD
129

130. P roblems
A
B
20kN/m
20×𝑥
6
𝑥 X
6m
X
𝑑𝑥
-
+
46.18kNm
-
6 3
Resultant BMD
130
24kNm
36kNm
ResultantBMD:

131. P roblems
Calculationofsupportreactions:
A
B
20kN/m
20×𝑥
6
𝑥 X
6m
X
𝑑𝑥
𝑅
𝐵
𝑅
𝐴
24 36
𝑀𝐴 =0
𝑅
1 2
𝐵 ×6+24=36+
2
×6×20×
3
×6
𝐵
6
𝑅 =
252
=42 kN
1
𝑅𝐴 +42=
2
×6×20
𝑅𝐴 =60−42=18kN
131

132. P roblems
SFD:
A
B
20kN/m
20×𝑥
6
𝑥 X
6m
X
𝑑𝑥
42kN
18kN
24 36
S.F
.@A=+
1
8kN
S.F
.@B=-42kN
SFDbetweenAandBis
aparabola.
S.F
.@XX=0
1 𝑥
18−
2
×𝑥×20×
6
= 0
18=
10𝑥2
6
𝑥=3.29 𝑚
Parabola
3.29m
132
18kN
42kN
SF
D

133. P roblems
ResultantBMD
&SFD:
A
B
20kN/m
20×𝑥
6
𝑥 X6m
X
𝑑𝑥
-
-
+
46.18kNm
Resultant BMD
24kNm
36kNm
3.29m
133
6 3=3.46m
18kN
42kN
SF
D

134. UNIT V
INDETERMINATE BEAMS: CONTINUOUS BEAMS
134

135. Continuo us beam wit h supports at differ e nt levels
• ConsiderthecontinuousbeamshowninaboveFigure.Let the
supportBbe𝛿1belowAandbelow C.
• ConsiderthespanAB:
• LetatanysectioninABdistant𝑥fromAthefreeandfixed bending
momentsbe𝑀𝑥 and𝑀𝑥
′ respectively.
• Hencethenetbendingmomentatthesectionisgiven by
𝑑2𝑦
𝐸𝐼
𝑑𝑥2 = 𝑀𝑥 −𝑀
𝑥
′
• Multiplyingby𝑥, weget
𝐸𝐼
𝑥
𝑑2𝑦
𝑑𝑥2 𝑥 𝑥
′
= 𝑀 𝑥−𝑀 𝑥
A C
𝑙1 𝑙
2
𝑀
𝐴
𝑀
𝐶
B𝑀
𝐵
𝛿
135
1

136. • 𝐸𝐼
𝑥
2
𝑑 𝑦
𝑑𝑥2 𝑥 𝑥
′
= 𝑀 𝑥−𝑀 𝑥
𝑑2𝑦
𝑙
1 𝑙
1
• Integratingfrom𝑥=0𝑡𝑜𝑥=𝑙1,we get,
𝐸𝐼 𝑥
𝑑𝑥2 = 𝑀𝑥𝑥 𝑑𝑥 −𝑀𝑥
′𝑥 𝑑𝑥
𝑙
1
0 0
0
𝑑𝑦
𝐸𝐼 𝑥.
𝑑𝑥
−𝑦
136
0
𝑙
1
𝑙1 𝑙1
= 𝑀𝑥𝑥 𝑑𝑥 −𝑀𝑥
′𝑥 𝑑𝑥
0 0
−−−(1)
C o n t i n u o u s b e a m w i t h s u p p o r t s a t d i f f e r e n t l e v e l s

137. • Butit maybesuchthat
At𝑥 =0, deflection𝑦 =0
𝑑𝑥
• At𝑥=𝑙1,𝑦 =−𝛿1;𝑎𝑛𝑑 𝑠𝑙𝑜𝑝𝑒𝑎𝑡𝐵 𝑓𝑜𝑟𝐴𝐵, 𝑑𝑦
=𝜃𝐵𝐴
• 𝑥
𝑙1
0
𝑀 𝑥𝑑𝑥 =𝑎 𝑥
1 1 =MomentofthefreeB.M.D.onABaboutA.
•
𝑙1
0 𝑥 1
′
1
′
′
𝑀 𝑥𝑑𝑥 =𝑎 𝑥 =MomentofthefixedB.M.D.onABaboutA.
A C
𝑙1 𝑙2
𝑀
𝐴
𝑀
𝐶
B𝑀
𝐵
𝛿1
𝑥
137
Co ntin uo u s b eam wit h sup p o rts at d iffer e nt levels

138. 𝑑𝑦
𝐸𝐼 𝑥.
𝑑𝑥
−𝑦
0
𝑙
1
𝑙1 𝑙1
= 𝑀𝑥𝑥 𝑑𝑥 −𝑀𝑥
′𝑥 𝑑𝑥
0 0
−−(1)
• Thereforetheequation(1)issimplifiedas,
𝐸𝐼 𝑙1𝜃𝐵𝐴 − −𝛿1 =𝑎1𝑥1 −𝑎′𝑥1
′.
1
1
But𝑎′ =areaofthefixedB.M.D.onAB=
𝑀 𝐴 +
𝑀 𝐵
2
𝑙
1
𝑥1
′ =CentroidofthefixedB.M.D.fromA=
𝑀 𝐴 +2𝑀 𝐵 𝑙
1
𝑀 𝐴 +𝑀 𝐵 3
Continuo us beam wit h supports at differ e nt levels
138

139. • Therefore,
𝟏
𝒂′ 𝒙𝟏
′ =
(𝑴𝑨 +𝑴𝑩 ) 𝑴 𝑨 +𝟐𝑴
𝑩 𝒍𝟏×
𝒍
𝟏
𝟐 𝑴 𝑨 +𝑴 𝑩
𝟑
=(𝑴𝑨 +𝟐𝑴𝑩 )
𝟏
𝒍
𝟐
𝟔
SimilarlybyconsideringthespanBCandtakingCasoriginit canbe shown
that,
𝜃𝐵𝐶 =slopefor spanCBatB
C o n t i n u o u s b e a m w i t h s u p p o r t s a t d i f f e r e n t l e v e l s
∴𝐸𝐼(𝑙𝜃1 𝐵𝐴 + 1
𝛿 ) =𝑎 𝑥 − 𝑀 +2𝑀
1 1 𝐴
𝐵
𝑙
1
2
6
𝐵
𝐴
6𝐸𝐼𝜃 =
6𝑎 𝑥
1 1
−
6𝐸𝐼𝛿 1
𝑙
1 𝑙
1
1
− 𝑀𝐴 +2𝑀𝐵 𝑙 −−−(2)
6𝐸𝐼𝜃𝐵𝐶 =
6𝑎 𝑥 6𝐸𝐼
𝛿
2 2 2
𝑙
2 𝑙
2
𝐶 𝐵 2
139
− − 𝑀 +2𝑀 𝑙 −−−(3)

140. • But𝜃𝐵𝐴 = −𝜃𝐵𝐶 asthedirectionof𝑥fromAforthespanAB,
andfromCforthespanCBareinoppositedirection.
• Andhence,𝜃𝐵𝐴+𝜃𝐵𝐶 =0
C o n t i n u o u s b e a m w i t h s u p p o r t s a t d i f f e r e n t l e v e l s
6𝐸𝐼𝜃𝐵𝐴 =
𝑙
1
6𝑎 𝑥 6𝐸𝐼𝛿
1 1 1
𝑙
1
𝐴 𝐵 1
− − 𝑀 +2𝑀 𝑙 −−−(2)
6𝐸𝐼𝜃𝐵𝐶 =
6𝑎 𝑥
2 2 6𝐸𝐼𝛿 2
𝑙
2 𝑙
2
− − 𝑀𝐶 +2𝑀
𝐵
2
𝑙 −−−(3)
Addingequations(2)and(3),weget
6𝐸𝐼(𝜃𝐵𝐴+𝜃𝐵𝐶)
=
6𝑎1𝑥1
+
6𝑎2𝑥2
−
6𝐸𝐼𝛿1
−
6𝐸𝐼𝛿2
𝑙1 𝑙2 𝑙1 𝑙2
− 𝑀𝐴𝑙1 +2𝑀𝐵 𝑙1+𝑙2 +𝑀𝑐𝑙2
140

141. C o n t i n u o u s b e a m w i t h s u p p o r t s a t d i f f e r e n t l e v e l s
6𝐸𝐼(𝜃𝐵𝐴+𝜃𝐵𝐶)
=
6𝑎1𝑥1
+
6𝑎2𝑥2
−
6𝐸𝐼𝛿1
−
6𝐸𝐼𝛿2
𝑙1 𝑙2 𝑙1 𝑙2
− 𝑀𝐴𝑙1 +2𝑀𝐵 𝑙1+𝑙2 +𝑀𝑐𝑙2
0=
6𝑎 𝑥
1 1
𝑙
1
+
𝑙
2
−
6𝑎 𝑥 6𝐸𝐼𝛿
2 2 1
𝑙
1
−
6𝐸𝐼𝛿 2
𝑙
2
− 𝑀𝐴𝑙1 +2𝑀𝐵 𝑙1
+𝑙2 +𝑀 𝑙
𝑐2
𝑀𝐴𝑙1 +2𝑀𝐵 𝑙1
+𝑙2 +𝑀 𝑙
𝑐2 =
6𝑎1𝑥1
+
6𝑎2𝑥2
− 6𝐸𝐼
𝑙1 𝑙2
𝛿1
+
𝛿2
𝑙1 𝑙2
141

142. • ThefollowingFigureshowsa continuousbeamcarryingan
externalloading.If the supportB sinksby 0.25cm belowthe
levelof the othersupportsfind supportmoments.TakeI for
section=15000cm4 and E=2x103t/cm2.
P r o b l e m s
2t/m
4m
142
4m 4m
A 4t/m B C D

143. • ThetheoremofthreemomentsfortwospansABandBCisas follows,
• ConsiderthespansABandBC,
• 𝑀𝐴 =0
• 𝛿1 =+0.25cm
• 𝛿2 =+0.25cm
P roblems
𝑀𝐴𝑙1 +2𝑀𝐵 𝑙1+𝑙2 +𝑀𝑐𝑙2 =
6𝑎1𝑥1
+
6𝑎2𝑥2
−6𝐸𝐼
𝛿1
+
𝛿2
𝑙
1 𝑙
2 𝑙
1 𝑙
2
2t/m
4m 4m
A 4t/m B C D
0.25cm
4m
143

144. 2
• 𝑎1=3
×4×8
2
• 6𝑎1𝑥1
=
6×3×4×8×2
=64
𝑙1 4
6𝑎 𝑥
𝑙
2
6×
2
×4×8×2
4
• 2 2
= 3
=64
P roblems
6𝐸𝐼=
6×2×103×15000
1002
=18000t𝑚2
8tm 8tm
4tm
FreeBMD
2t/m
4m 4m 4m
A 4t/m B C D
0.25cm
144

145. • ∴0+2𝑀𝐵 4+4 +4𝑀𝐶 =64+64−18000
• ∴16𝑀𝐵+4𝑀𝐶 =128−22.5
• 16𝑀𝐵+4𝑀𝐶 =105.5
• 4𝑀𝐵+𝑀𝐶 =26.375−−−−(1)
P roblems
8tm 8tm
𝑀 𝑙 +2𝑀 𝑙 +𝑙 +𝑀 𝑙
𝐴 1 𝐵 1 2 𝑐2
𝑙
1 𝑙
2
=
6𝑎1𝑥1
+
6𝑎2𝑥2
− 6𝐸𝐼
𝛿1
+
𝛿2
0.25
𝑙10.25
𝑙2
400
+400
4tm
2t/m
4m 4m 4m
A 4t/m B C D
0.25cm
145

146. • NowconsiderthespansBCandCD,
• 𝑀𝑑 =0,
• 𝛿1=−0.25cm
• 𝛿2=0
P r o b l e m s
4tm
2t/m
4m
8tm
4m
A 4t/m B C D
0.25cm
4m
8tm
146

147. 𝑀𝐵 ×4+2𝑀𝐶 4+4 +0=64+32−18000
• ∴4𝑀𝐵+16𝑀𝐶 =96+11.25
• 4𝑀𝐵+16𝑀𝐶 =107.25−−−−(2)
P r o b l e m s
8tm 8tm
𝑀𝐴𝑙1 +2𝑀𝐵 𝑙1
+𝑙2 +𝑀 𝑙
𝑐2
𝑙
1 𝑙
2
=
6𝑎1𝑥1
+
6𝑎2𝑥2
− 6𝐸𝐼
𝛿1
+
𝛿2
−0.
𝑙1 𝑙2
25
+
0
400 400
4tm
2t/m
4m 4m 4m
A 4t/m B C D
0.25cm
147

148. • 4𝑀𝐵+𝑀𝐶 =26.375 −−−−(1)
• 4𝑀𝐵+16𝑀𝐶 =107.25−−−−(2)
• Solving(1)and(2),weget,
• 𝑀𝐵 =5.24tm hogging .
• 𝑀𝐶 =5.39tm hogging .
148
P r o b l e m s

149. P r o b l e m s
+
5.24tm
-
5.39tm
-
8tm 8tm
+ 4tm
+
BMD
2t/m
4m 4m 4m
A 4t/m B C D
0.25cm
149

150. B
A
V
Fixed beam wit h ends at differ e nt levels (Effect of
sinking of supports) V
𝑀
𝐴
𝑀
𝐵
𝛿
150
𝑀𝐴 isnegative(hogging)and𝑀𝐵 ispositive(sagging).Numerically
𝑀𝐴 and𝑀𝐵 areequal.
LetVbethereactionateachsupport.

151. B
A
V
F i x e d b e a m w i t h e n d s a t d i f f e r e n t l e v e l s ( E f f e c t
o f s i n k i n g o f s u p p o r t s ) V
𝑀
𝐴
𝑀
𝐵
𝛿
𝑑4𝑦
Consideranysectiondistance𝑥fromtheendA.
Sincetherateofloadingiszero,wehave,withtheusualnotations
𝐸𝐼
𝑑𝑥4 =0
Integrating,weget,
𝑑3𝑦
Shearforce=𝐸𝐼𝑑𝑥3 =𝐶1
Where𝐶1isaconstant
At𝑥 =0, 𝑆.𝐹.=+V
∴𝐶1=V
𝑥
151

152. B
A
V
F i x e d b e a m w i t h e n d s a t d i f f e r e n t l e v e l s ( E f f e c t
o f s i n k i n g o f s u p p o r t s ) V
𝑀
𝐴
𝑀
𝐵
𝛿
𝑑2𝑦
B.M.atanysection=𝐸𝐼𝑑𝑥2 =𝑉𝑥 +𝐶1
At𝑥 =0, 𝐵. 𝑀.=−𝑀𝐴
∴ 𝐶2=−𝑀𝐴
𝑑2𝑦
∴𝐸𝐼
𝑑𝑥2 =𝑉𝑥 −𝑀𝐴
Integratingagain,
𝑑𝑥 2
𝐸𝐼𝑑𝑦
=𝑉
𝑥2 −𝑀𝐴𝑥 +𝐶3(Slopeequation)
𝑑𝑦
Butat𝑥 = 0, 𝑑𝑥
=0 ∴𝐶3=0
𝑥
152

153. B
A
F i x e d b e a m w i t h e n d s a t d i f f e r e n t l e v e l s ( E f f e c t
o f s i n k i n g o f s u p p o r t s ) V
𝑀
𝐴
𝑀
𝐵
𝛿
V
Integratingagain,
3
𝐸𝐼𝑦 = − 𝐴
𝑉𝑥 𝑀 𝑥2
6 2 4
+𝐶 ------ (Deflectionequation)
Butat𝑥=0,𝑦 = 0
∴𝐶4=0
At𝑥=𝑙,𝑦 = −𝛿
𝑉𝑙
3
−𝐸𝐼𝛿 =
6
−
𝑀 𝐴 𝑙
2
2
−−−−−−−−(i)
𝑙
𝑥
153

154. B
A
V
F i x e d b e a m w i t h e n d s a t d i f f e r e n t l e v e l s ( E f f e c t
o f s i n k i n g o f s u p p o r t s ) V
𝑀
𝐴
𝑀
𝐵
𝛿
𝑑𝑦
ButwealsoknowthatatB,𝑥=𝑙
𝑎𝑛𝑑 𝑑𝑥
=0
𝑑𝑥 2
AndsubstituteinslopeEq. 𝐸𝐼𝑑𝑦
=𝑉
𝑥2 −𝑀𝐴𝑥
𝑉𝑙
2
∴ 0 =
2
−𝑀𝐴𝑙
∴𝑉 =
2𝑀𝐴
−−−−−−−− ii
𝑙
SubstitutingindeflectionEq.(i)i.e.,−𝐸𝐼𝛿 =𝑉𝑙3
−𝑀𝐴𝑙2
;wehave,
2𝑀
𝐴
𝑙
3
−𝐸𝐼𝛿 = × −
6 2
𝑀𝐴𝑙2
𝑙
𝑥
2 154

155. B
A
V
F i x e d b e a m w i t h e n d s a t d i f f e r e n t l e v e l s ( E f f e c t
o f s i n k i n g o f s u p p o r t s ) V
𝑀
𝐴
𝑀
𝐵
𝛿
𝐸𝐼𝛿 = 𝐴
𝑀 𝑙2
6
∴
𝑀
𝐴 =
6𝐸𝐼𝛿
𝑙
2
𝑑2𝑦
Hencethelawforthebendingmomentatanysectiondistant x
fromAisgivenby
,
𝑀 =𝐸𝐼
𝑑𝑥2 =V𝑥−𝑀𝐴
𝑙
∴𝑀 =
2𝑀𝐴
𝑥−
6𝐸𝐼𝛿
𝑙
2
𝑙
155
155

156. B
A
V
F i x e d b e a m w i t h e n d s a t d i f f e r e n t l e v e l s ( E f f e c t
o f
s i n k i n g o f s u p p o r t s ) V
𝑀
𝐴
𝑀
𝐵
𝛿
ButforB.M.atB,putx=l,
∴
𝑀
𝐵
𝑙
=
2𝑀𝐴
×𝑙
−
6𝐸𝐼𝛿
=
12𝐸𝐼𝛿
−
6𝐸𝐼𝛿
=
6𝐸𝐼𝛿
𝑙
2 𝑙
2 𝑙
2 𝑙
2
Hencewhentheendsofafixedbeamareatdifferent levels,
Thefixingmomentateachend=
6𝐸𝐼𝛿
𝑙
2 numerically.
Atthehigherendthismomentisahoggingmomentandat the
lowerendthismomentisasaggingmoment.
𝑙
156
156

157. P r o b l e m s
A B
3m
157
2m
• Afixed beamof span5 metrescarriesa concentratedloadof 20 t
at3 metersfromthe left end. If the rightend sinksby 1 cm, find
the fixing momentsat the supports.For the beamsectiontake
I=30,000cm4and E=2x103t/cm2.Find alsothe reactionat the
supports.
20 t
157

158. • Therightendsinksby 1 cm,find the fixing momentsat the
supports.
P roblems
A B
3m 2m
• Afixed beamof span5 metrescarriesa concentratedloadof 20 t
at3 metersfromthe left end.
20 t
1cm
158
158

159. • 𝑀𝐴 =−Wa𝑏2
−6𝐸𝐼𝛿
𝑙
2
• =−
𝑙2
20×3×22
52 +
6×2×103×30,000×1
52×1002
tm
• =− 9.6+0.48 tm=-10.08tm(hogging)
• 𝑀𝐵
=−W𝑏𝑎2
+6𝐸𝐼𝛿
𝑙2 𝑙2
• 52
= −20×2×32
+6×2×103×30,000×1
52×1002
tm
• = −14.4+0.48 tm=-13.92tm(hogging)
P roblems
A B
3m 2m
20t
1cm
𝑀
𝐴
𝑀
𝐵
159
159

160. • Reaction at A:
• 𝑀𝐵=0,
• 𝑉𝐴 × 5 + 13.92 − 10.08 − 20 × 2 = 0
• ∴ 𝑉𝐴 = 7.232 t
• Reaction at B:
• ∴ 𝑉𝐵 = 20 − 7.232 = 12.768 t.
P r o b l e m s
A B
3m 2m
20t
10.08
13.92
𝑉
𝐴
160
𝑉
𝐵
160