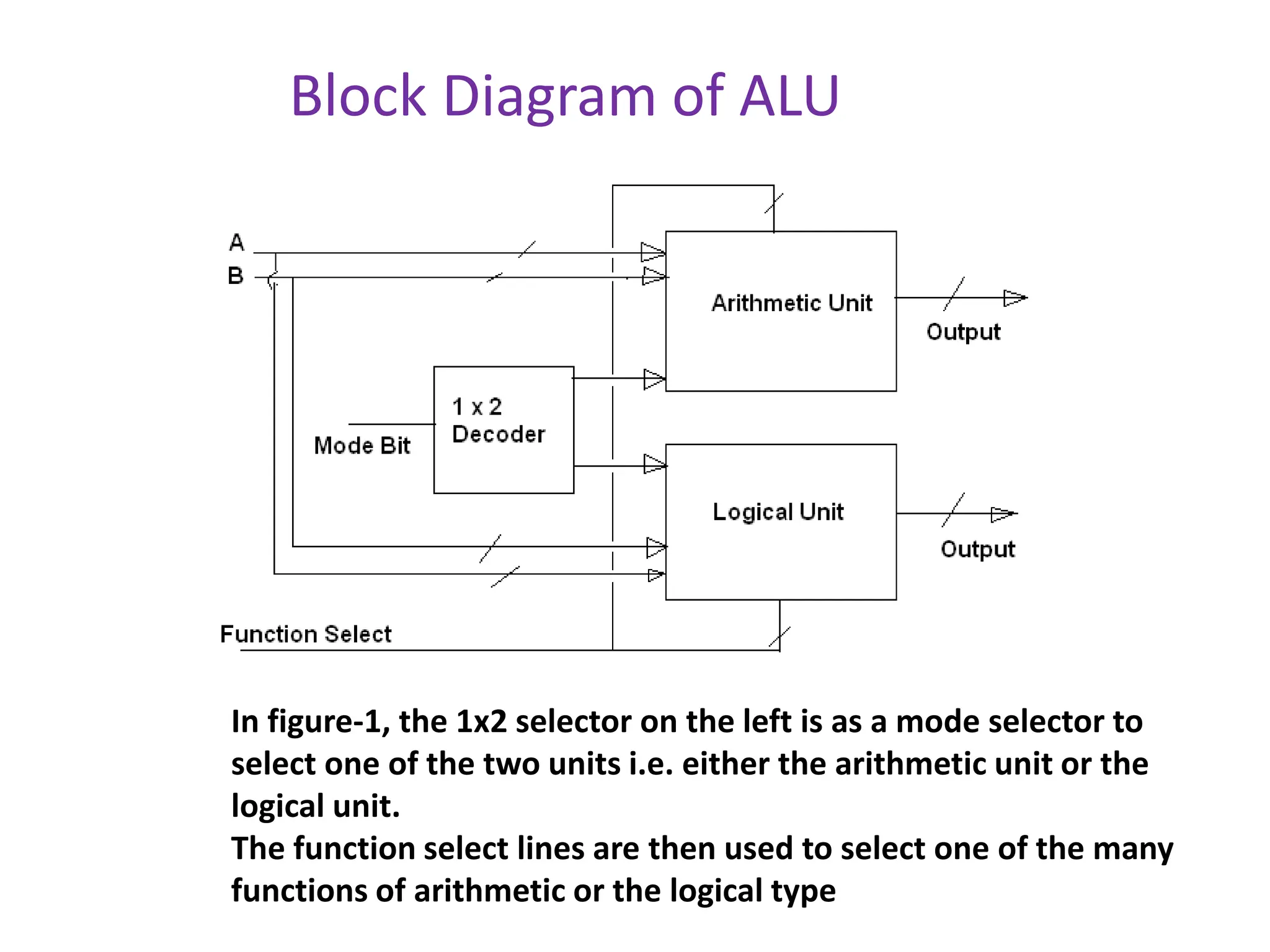
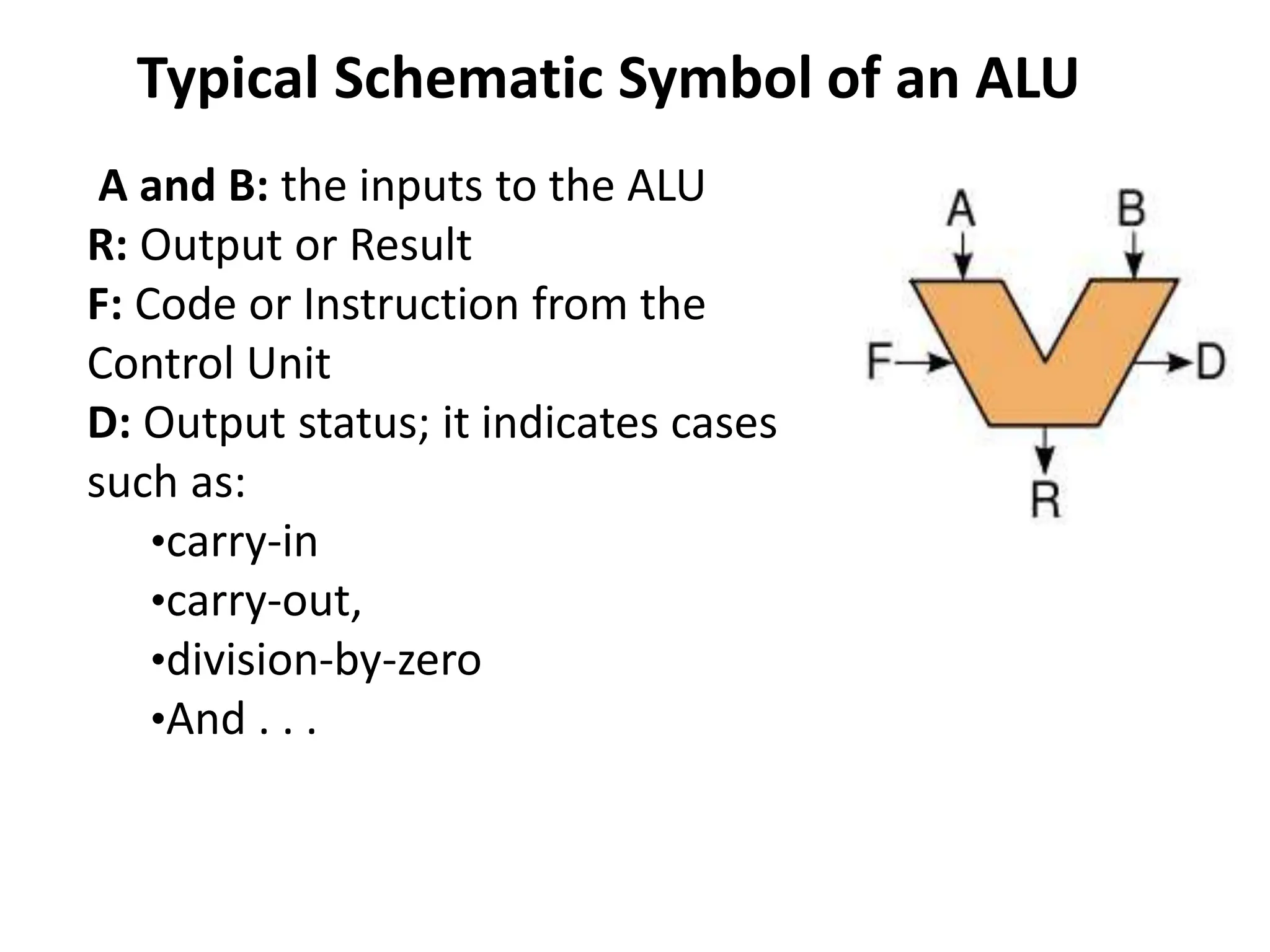
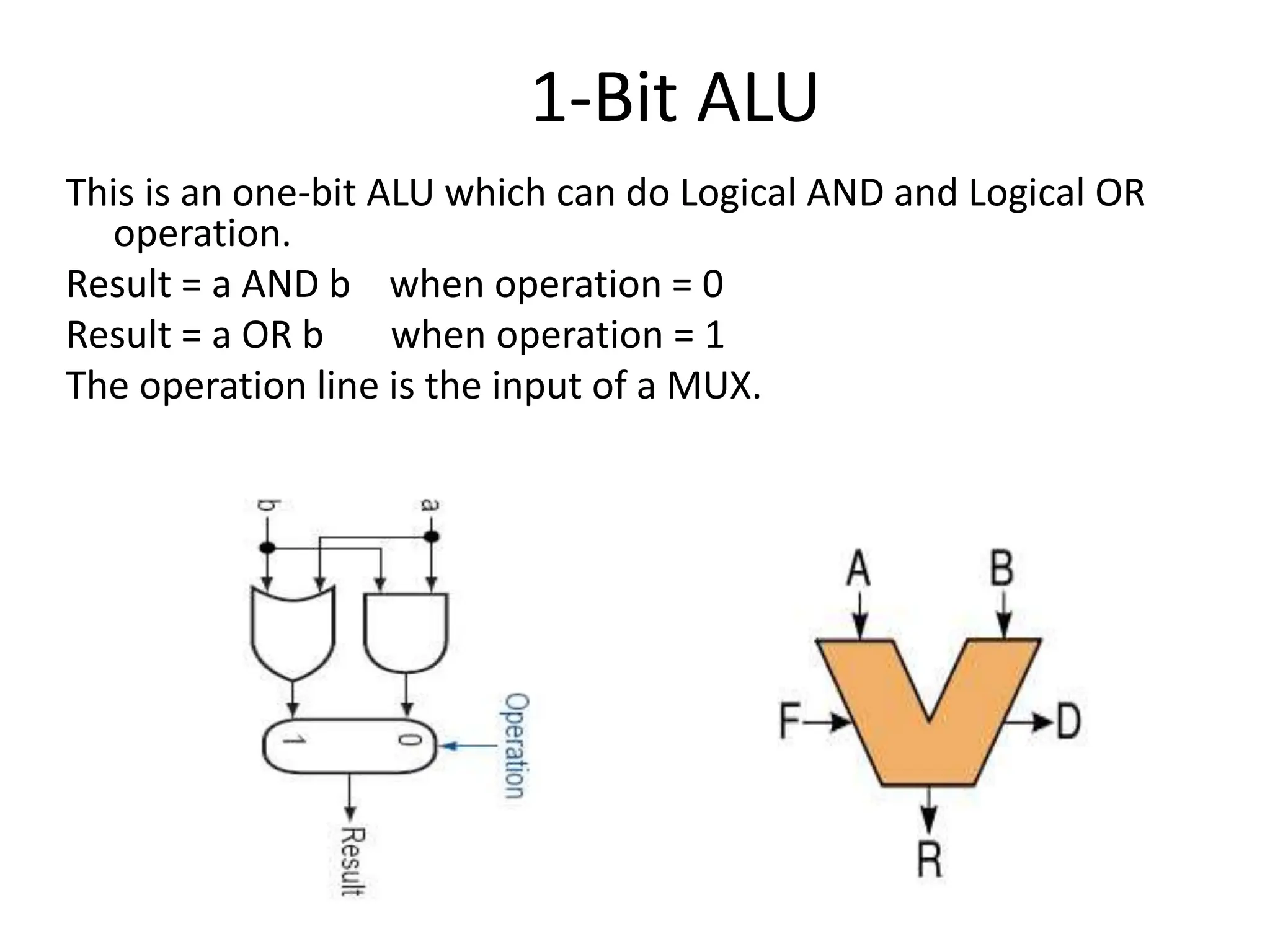
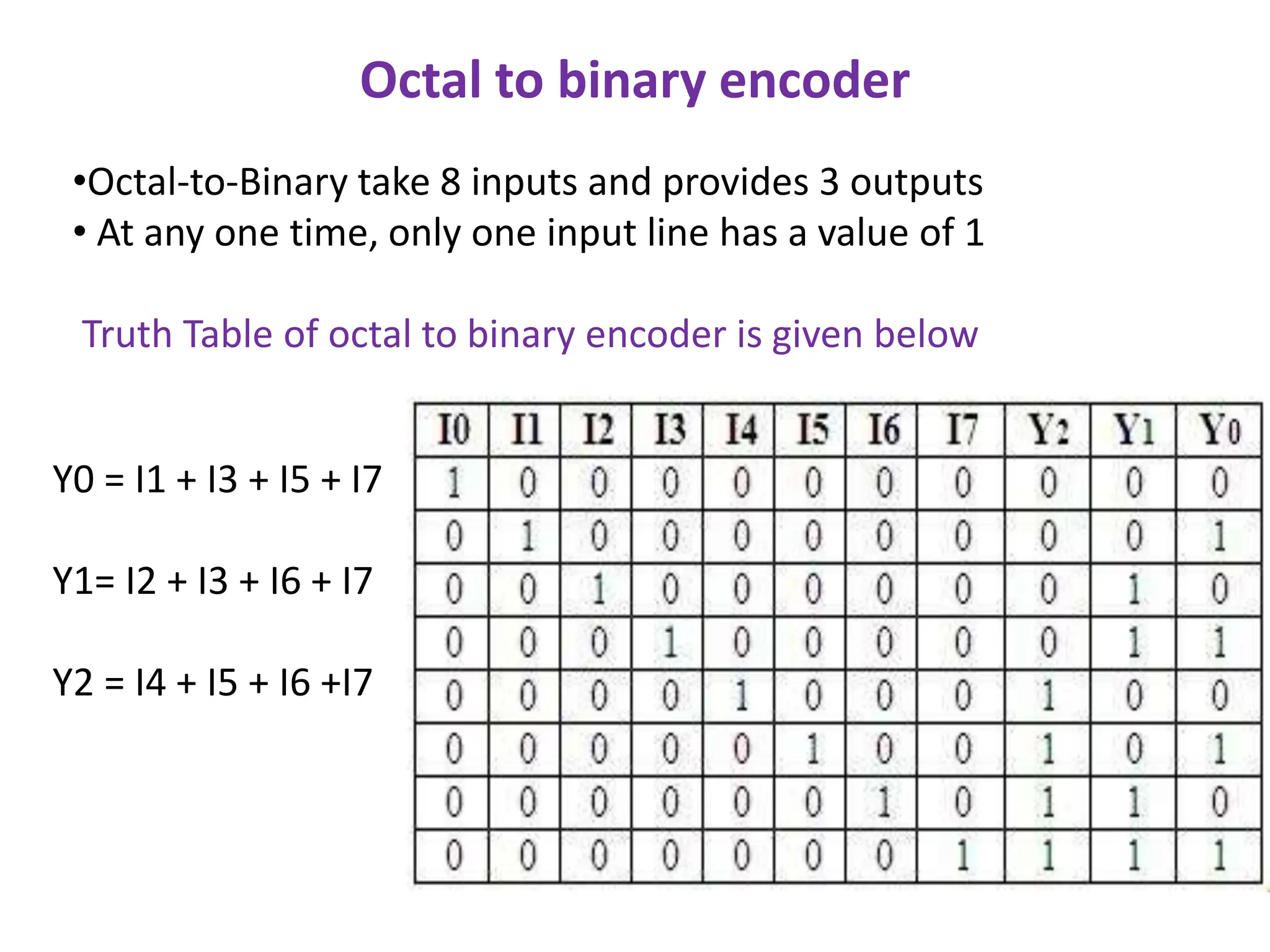
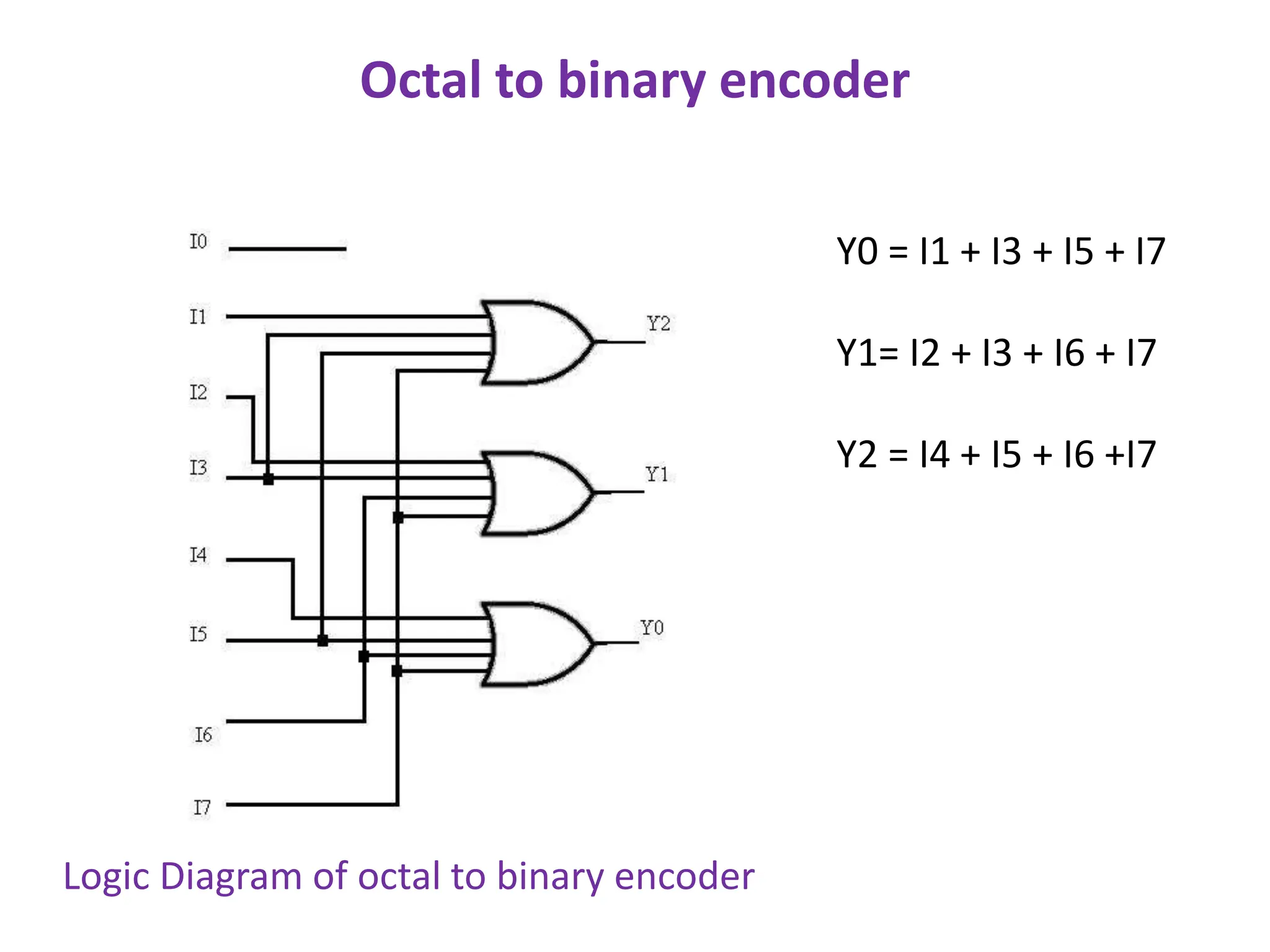
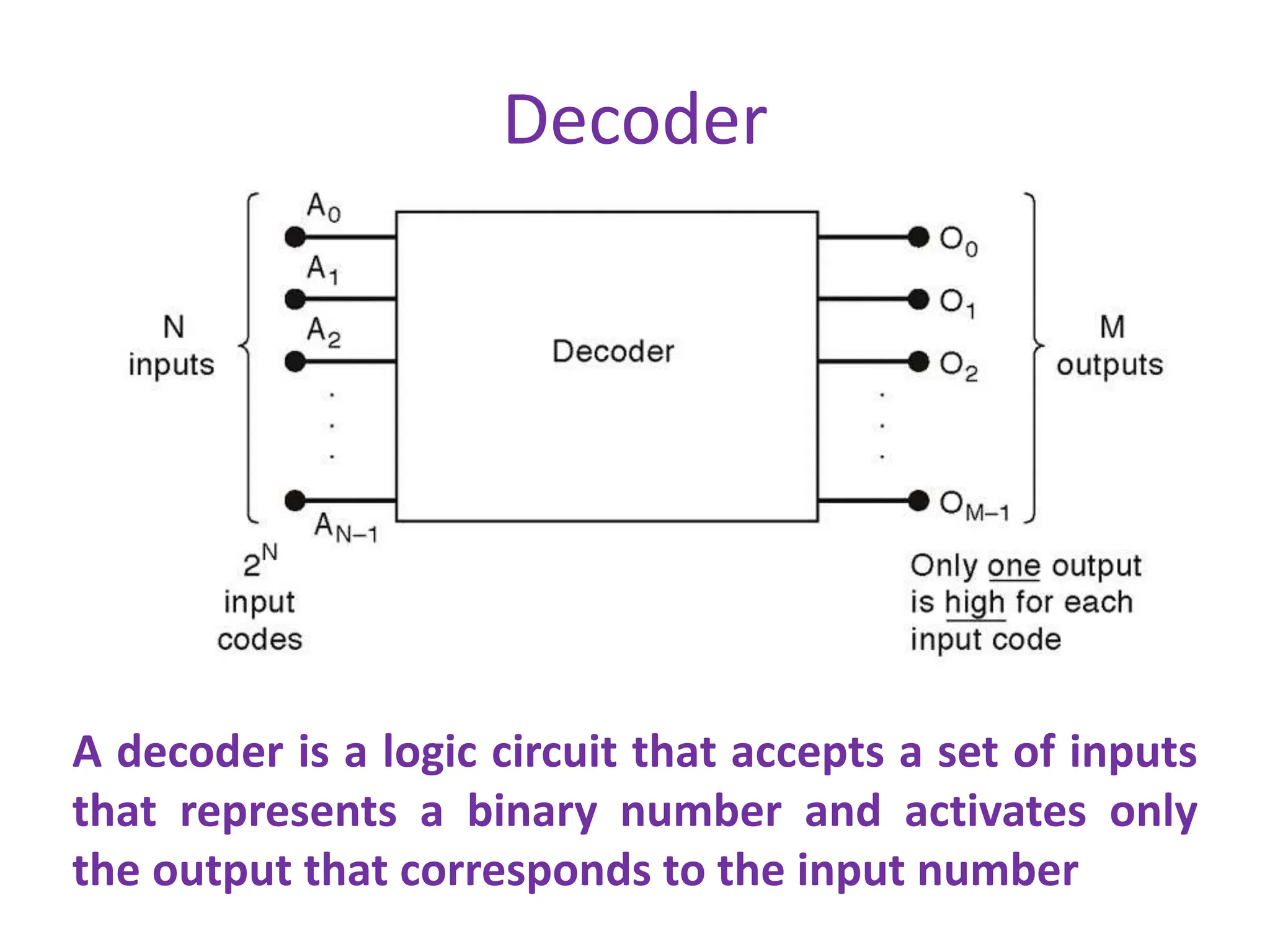
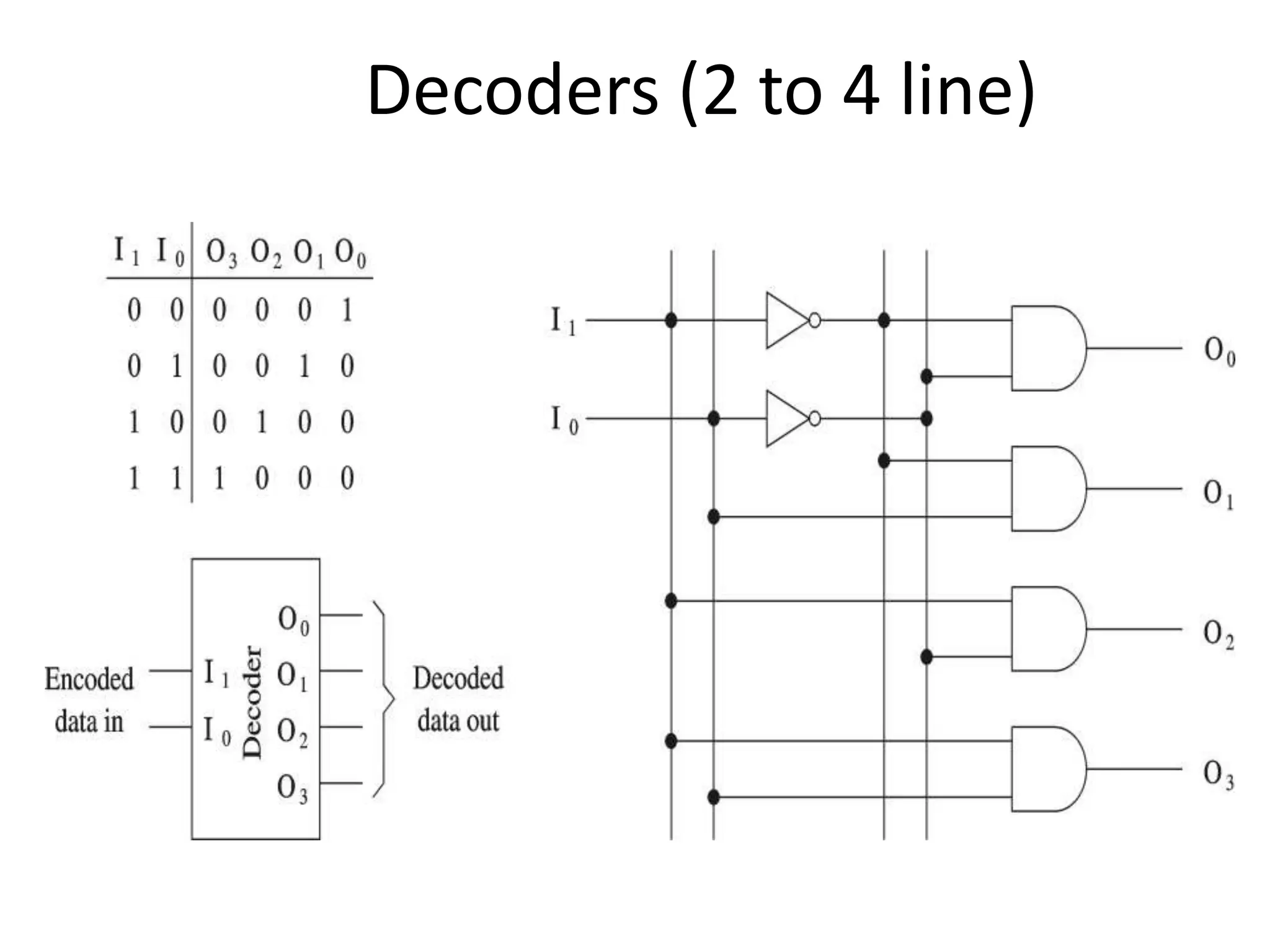
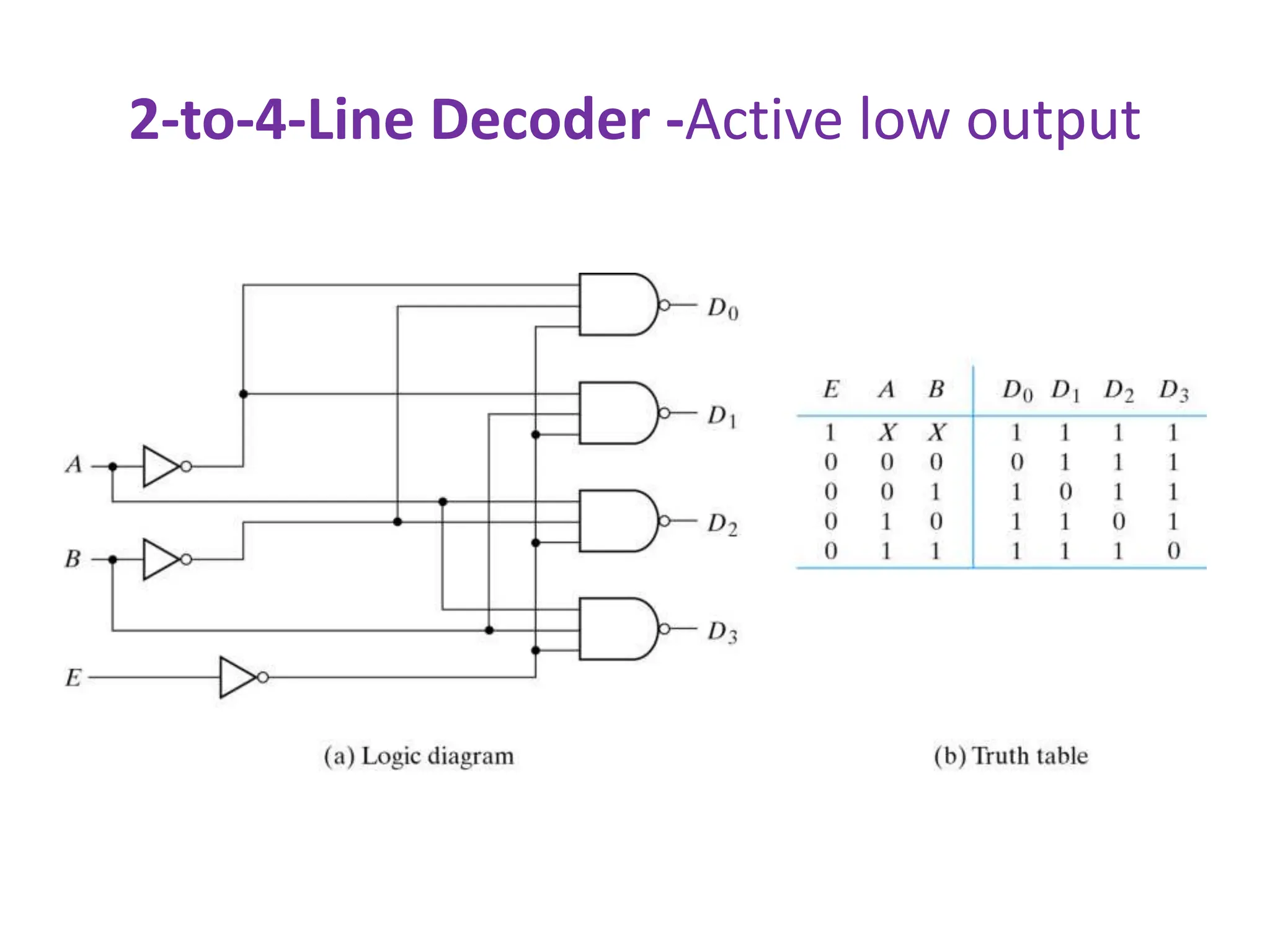
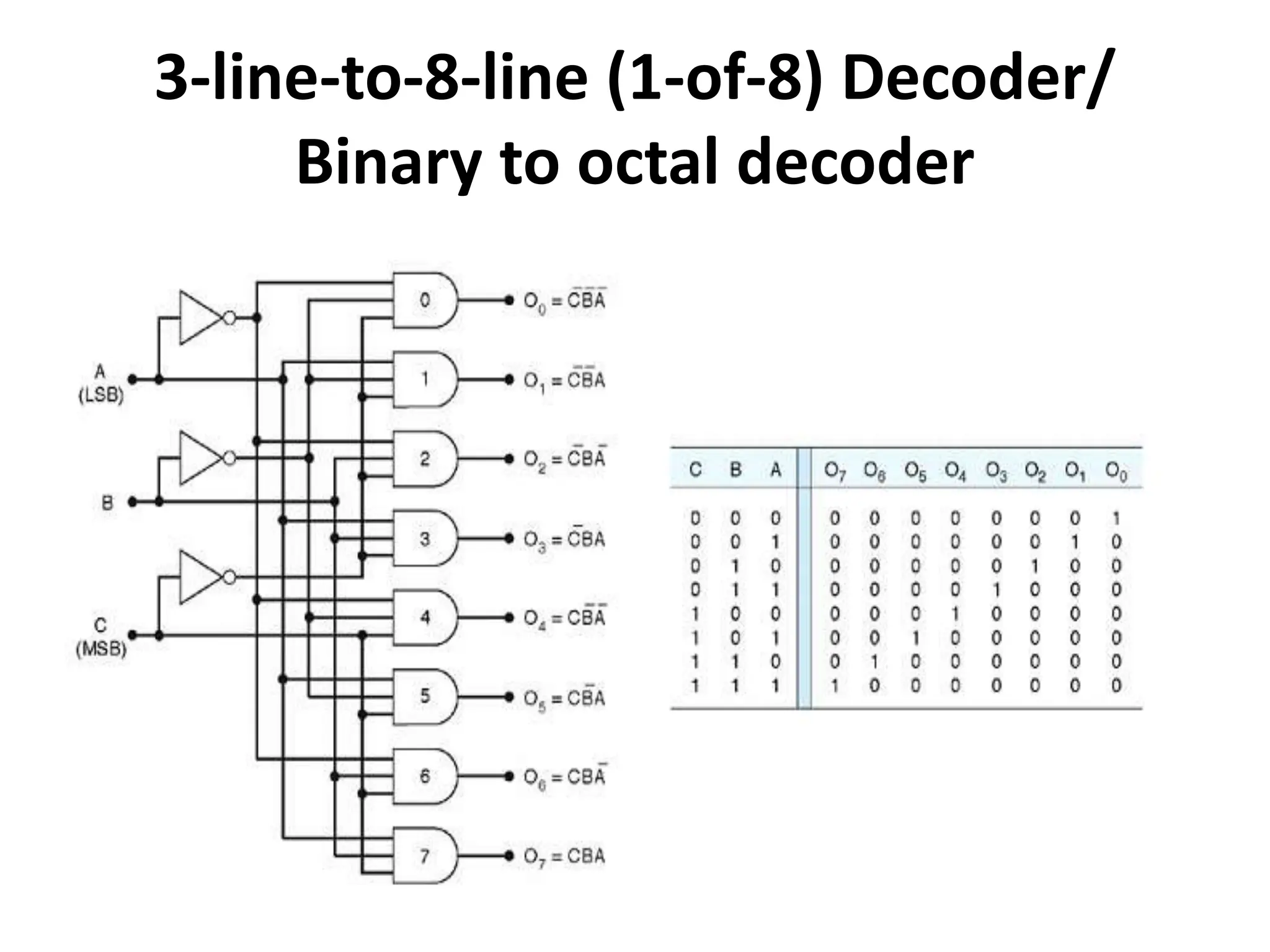
The document discusses the concepts of ripple-carry adders and carry look-ahead adders, explaining their mechanisms and delays in processing binary addition. It introduces the arithmetic logic unit (ALU), detailing its function in performing arithmetic and logical operations, as well as components like encoders and decoders used in digital circuits. Additionally, it describes the complexities associated with implementing CLA adders for larger bit sizes and presents examples of digital circuits including octal-to-binary encoders and BCD-to-decimal decoders.

1. N Bit Adders
A 16-bit ripple-carry adder
Cout of one adder is connected to Cin of the next stage.
These are called ripple-carry adders
Ripple-carry adders are slow due to the cumulative
propagation time of carry in different stages
Delay proportional to the number of bits

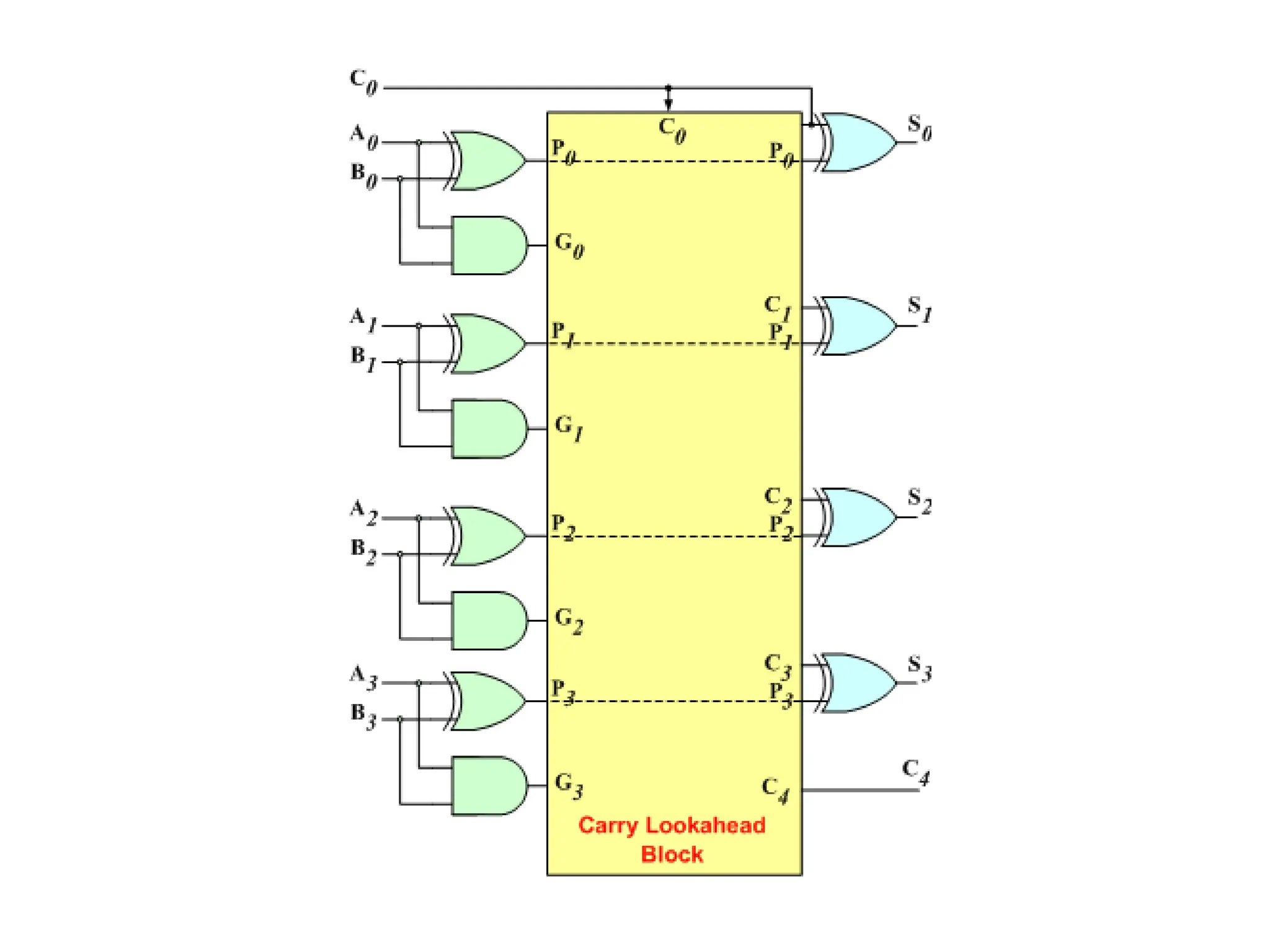
2. Si = Ai ⊕ Bi ⊕Ci-1= Pi ⊕ Ci-1 [Pi = Ai ⊕ Bi ]
Ci = AiBi + (Ai ⊕ Bi )Ci-1 = Gi + PiCi-1 [Gi = AiBi ]
Time delay = 3τ = (2n +1)

3. Carry look ahead adder
– Eliminate the delay of ripple-carry adders
– Carry-in’s are generated independently
carry signal will be generated in two cases:
1. if both bits Ai and Bi are 1
2. if either Ai or Bi is 1 and the carry-in Ci is 1
The Propagate P and generate G in a full-adder, is
given as:
• Pi = Ai ⊕ Bi Carry propagate
• Gi = AiBi Carry generate

4. Carry look ahead adder
• The new expressions for the output sum and the carryout
are given by:
• Si = Ai ⊕ Bi ⊕Ci-1= Pi ⊕ Ci-1 [Pi = Ai ⊕ Bi ]
• Ci = AiBi + (Ai ⊕ Bi )Ci-1 = Gi + PiCi-1 [Gi = AiBi ]
Let's apply these equations for a 4-bit adder
• C0 = G0 + P0C-1
• C1 = G1 + P1C0 = G1 + P1(G0 + P0C-1) = G1 + P1G0 + P1P0C-1
• C2 = G2 + P2C1 = G2 + P2G1 + P2 P1G0 + P2P1P0C-1
• C3 = G3 + P3C2 = G3 + P3G2 +P3P2G1 +P3P2 P1G0 +
P3P2P1P0C-1
These expressions show that C1, C2 and C3 do not depend on
its previous carry-in

5. Carry look ahead adder
• In general, the ith. carry output is expressed in the
form Ci = Fi (Pi’s, Gi’s , C-1)
• In other words, each carry signal is expressed as a
direct SOP function of C-1 ( carry input of first
stage)rather than its preceding carry signal.
• Since the Boolean expression for each output
carry is expressed in SOP form, it can be
implemented in two-level circuits.
• The 4-bit carry look-ahead (CLA) adder consists of
3 levels of logic:

6. Carry look ahead adder
• First level: Generates all the P & G signals. Four sets of P & G logic
(each consists of an XOR gate and an AND gate).
Pi = Ai ⊕ Bi Gi = AiBi
Output signals of this level (P’s & G’s) will be valid after 1τ
• Second level: The Carry Look-Ahead (CLA) logic block generates
the carry signals (C0,C1, C2 and C3) which consists of four 2-level
implementation logic circuits
Ci = AiBi + (Ai ⊕ Bi )Ci-1 = Gi + PiCi-1
Output signals of this level (C0,C1, C2 and C3) will be valid after 3τ
• Third level: Four XOR gates generate the sum signals (Si)
Si = Pi ⊕ Ci
• Output signals of this level (S0, S1, S2 and S3) will be valid after 4τ

7. Carry look ahead adder
• Thus, the 4 Sum signals (S0, S1, S2 & S3) will all be
valid after a total delay of 4τ compared to a delay
of (2n+1)τ for Ripple Carry adders
• For a 4-bit adder (n = 4), the Ripple Carry adder
delay is 9τ
• The disadvantage of the CLA adders is that the
carry expressions (and hence logic) become quite
complex for more than 4 bits
• Thus, CLA adders are usually implemented as 4-
bit modules that are used to build larger size
adders

9. ALU
• ALU stands for: Arithmetic Logic Unit
• An arithmetic logic unit (ALU) is a digital circuit
used to perform arithmetic and logic operations.
• It represents the fundamental building block of the
central processing unit (CPU) of a computer
• Examples of arithmetic operations are addition,
subtraction, multiplication, and division etc.
• Examples of logic operations are comparisons of
values such as NOT, AND, and OR etc.

10. In figure-1, the 1x2 selector on the left is as a mode selector to
select one of the two units i.e. either the arithmetic unit or the
logical unit.
The function select lines are then used to select one of the many
functions of arithmetic or the logical type
Block Diagram of ALU

11. Typical Schematic Symbol of an ALU
A and B: the inputs to the ALU
R: Output or Result
F: Code or Instruction from the
Control Unit
D: Output status; it indicates cases
such as:
•carry-in
•carry-out,
•division-by-zero
•And . . .

12. 1-Bit ALU
This is an one-bit ALU which can do Logical AND and Logical OR
operation.
Result = a AND b when operation = 0
Result = a OR b when operation = 1
The operation line is the input of a MUX.

13. Adding one more operation- one full adder to the
previous ALU
1-Bit ALU

14. Simple block diagram

15. Encoder/Decoder
ENCODER- a digital circuit that produces a binary output code
depending on which of its inputs are activated.
DECODER- a digital circuit that converts an input binary code
into a single numeric output.
A0
A1
A2
A3
A4
A5
A6
A7
ENCODER
O0
O1
O2
A0
A1
A2
O0
O1
O2
O3
O4
O5
O6
O7
DECODER
Only one input activated at a time
Binary coded output
Binary coded input
Only one output activated at a time

16. Encoder
• The process of converting from familiar symbols or
numbers to a coded format is called encoding.
• ENCODER- a digital circuit that produces a binary
output code depending on which of its input is
activated

17. Octal to binary encoder
•Octal-to-Binary take 8 inputs and provides 3 outputs
• At any one time, only one input line has a value of 1
Truth Table of octal to binary encoder is given below
Y0 = I1 + I3 + I5 + I7
Y1= I2 + I3 + I6 + I7
Y2 = I4 + I5 + I6 +I7

18. Y0 = I1 + I3 + I5 + I7
Y1= I2 + I3 + I6 + I7
Y2 = I4 + I5 + I6 +I7
Logic Diagram of octal to binary encoder
Octal to binary encoder

19. Decoder
A decoder is a logic circuit that accepts a set of inputs
that represents a binary number and activates only
the output that corresponds to the input number

20. Decoders (2 to 4 line)

21. 2-to-4-Line Decoder -Active low output

22. 3-line-to-8-line (1-of-8) Decoder/
Binary to octal decoder

23. 23
BCD -to- Decimal decoders
•The BCD- to-decimal decoder converts each BCD code into
one of Ten decimal digit indications.
• It is frequently referred as a 4-line -to- 10 line decoder
•The method of implementation is that only ten decoding
gates are required because the BCD code represents only the
ten decimal digits 0 through 9.
•Each of these decoding functions is implemented with NAND
gates to provide active -LOW outputs. If an active HIGH
output is required, AND gates are used for decoding