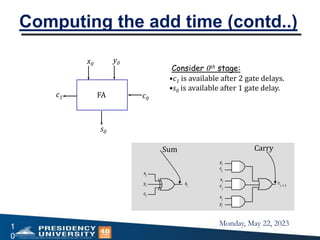
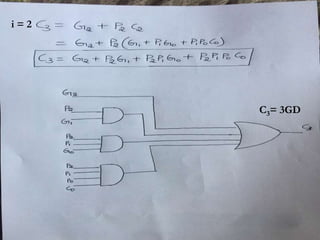
This document discusses arithmetic units and operations in digital computers. It covers carry lookahead adders, signed-operand multiplication using sign extension, Booth's multiplication algorithm, and restoring division. For addition, it explains how carry lookahead adders can perform addition faster than ripple carry adders by computing propagate and generate signals in one gate delay. It also discusses how signed numbers are multiplied by extending the sign bit and provides an example of Booth's algorithm. For division, it outlines the restoring division algorithm which performs long division with a shift-and-subtract approach over multiple cycles.