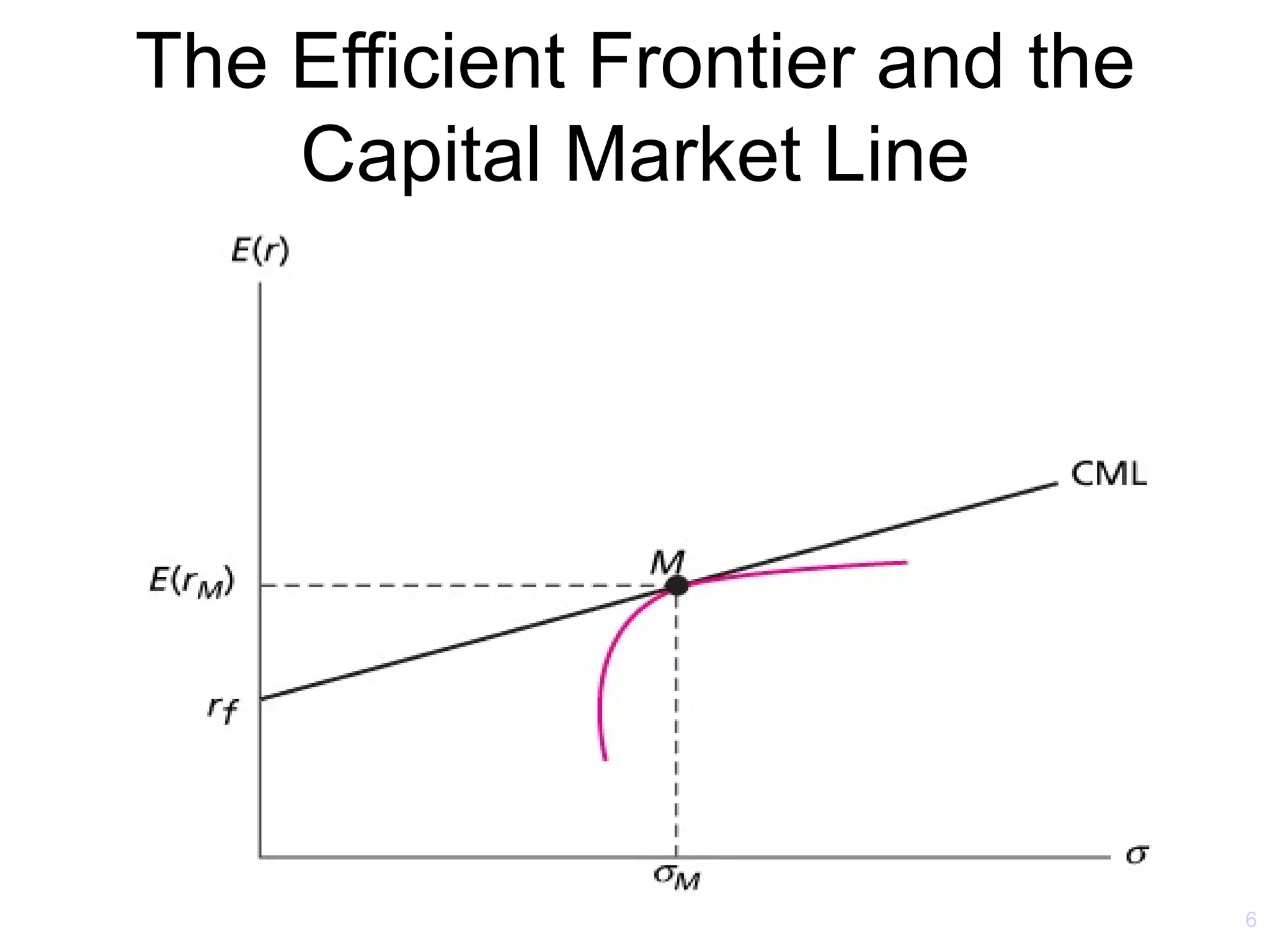
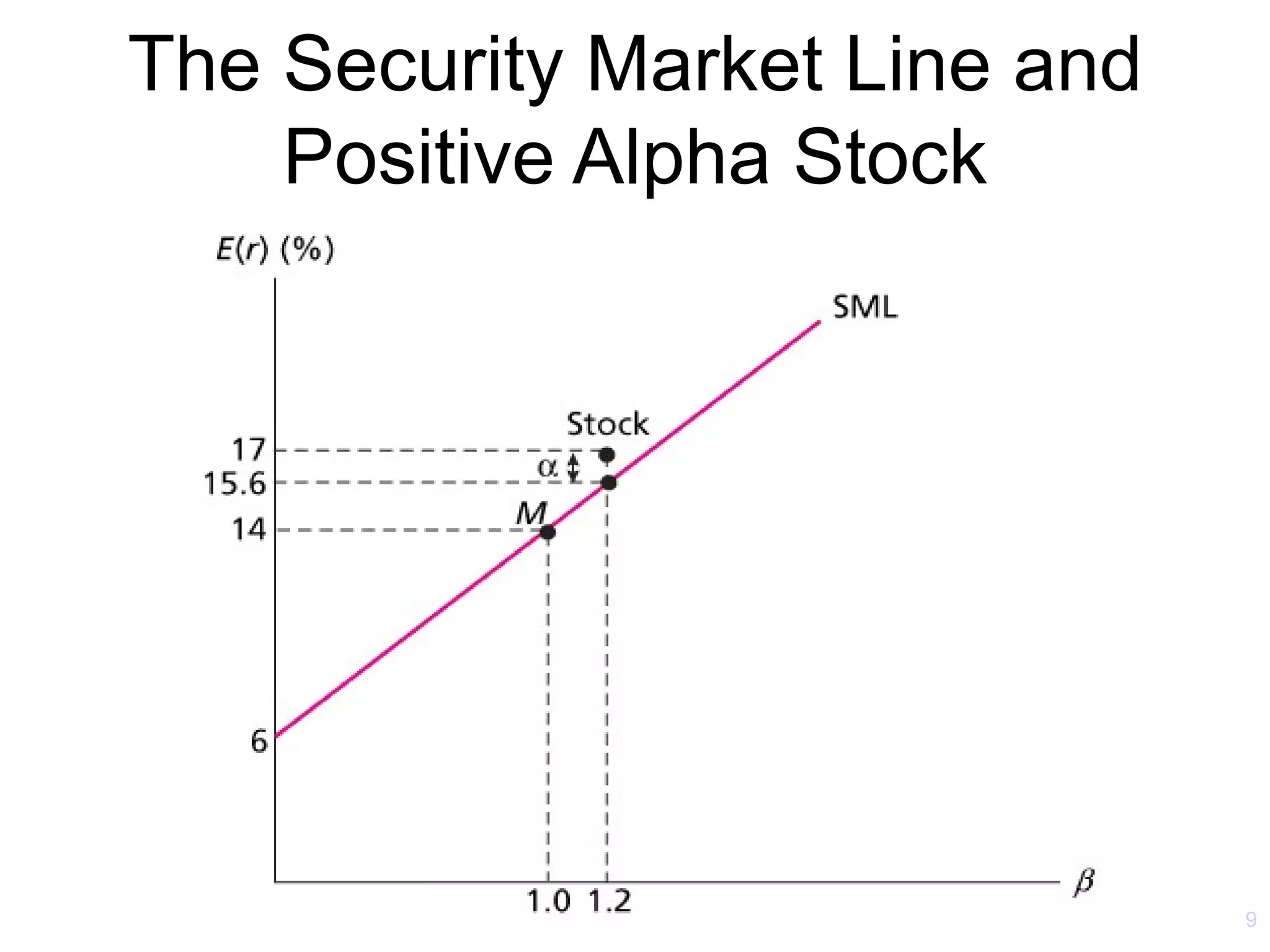
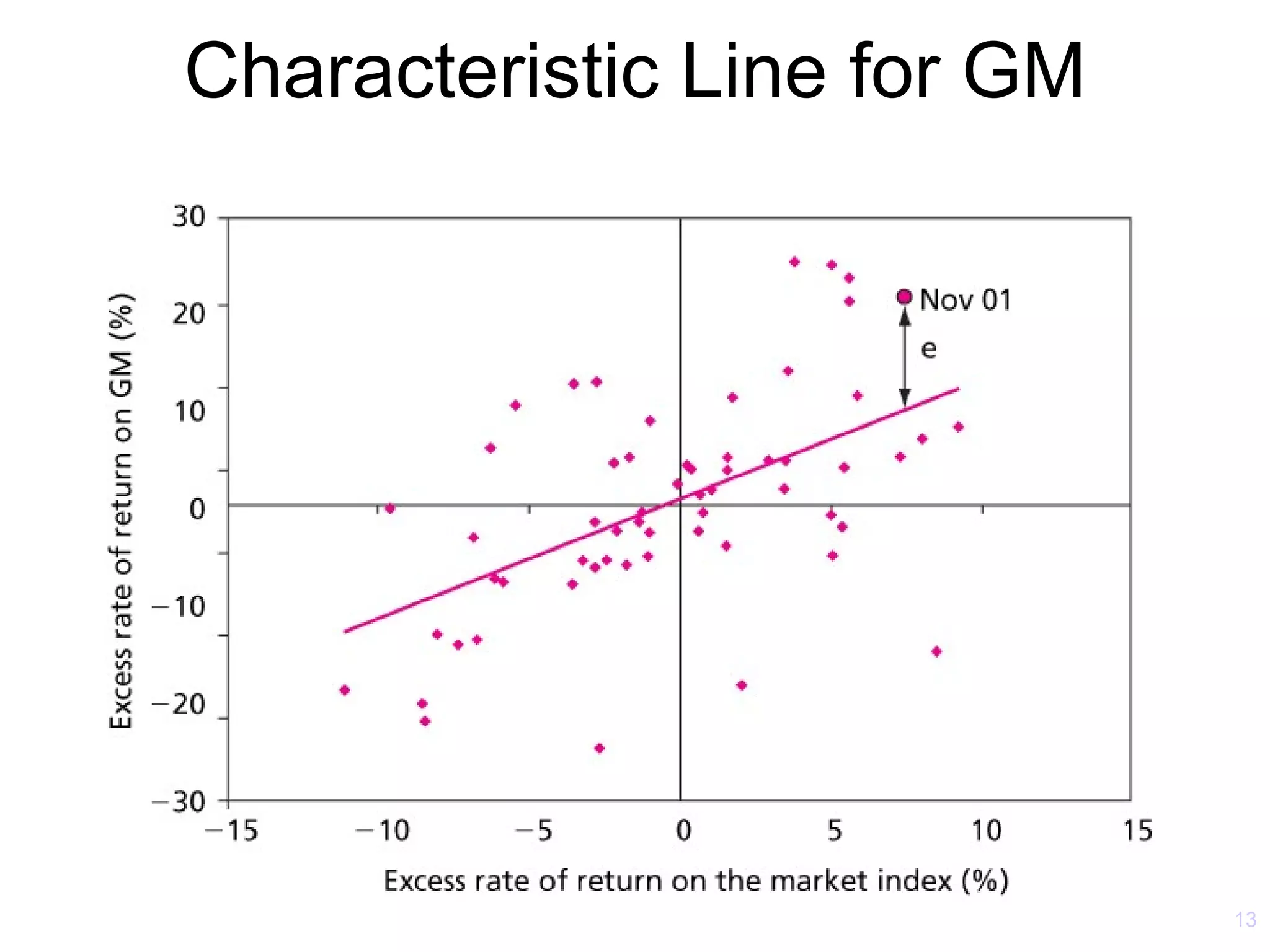
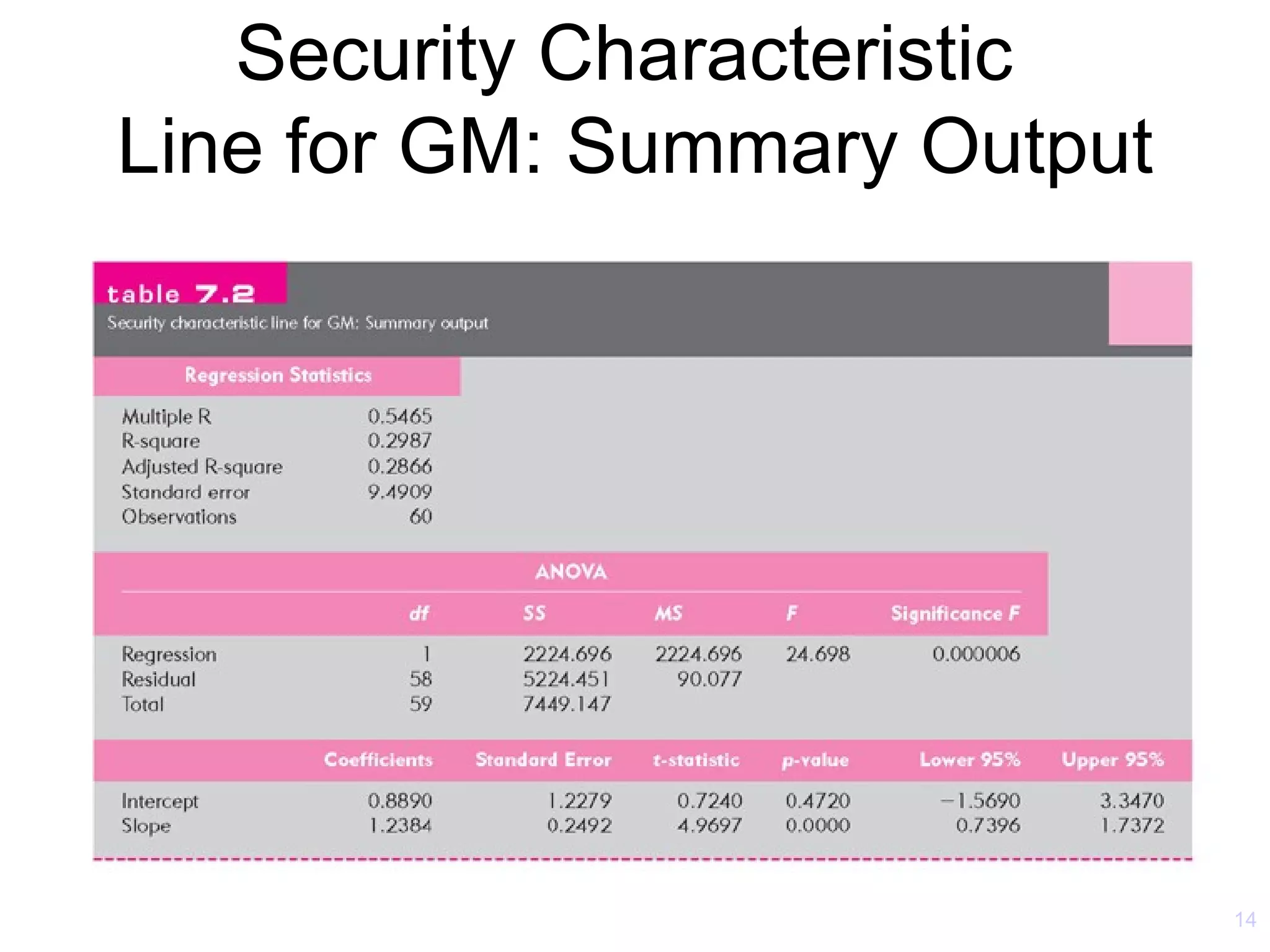
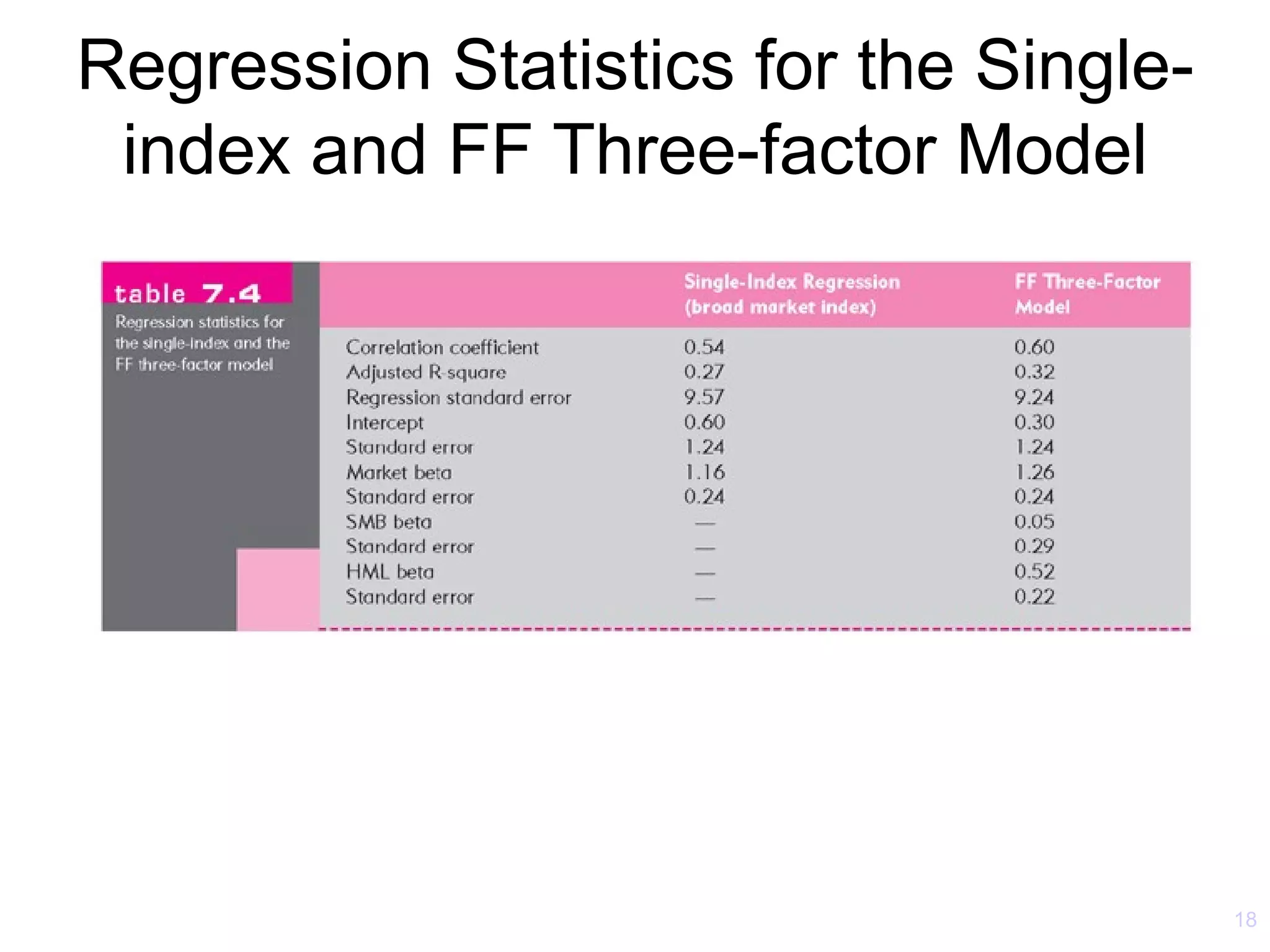
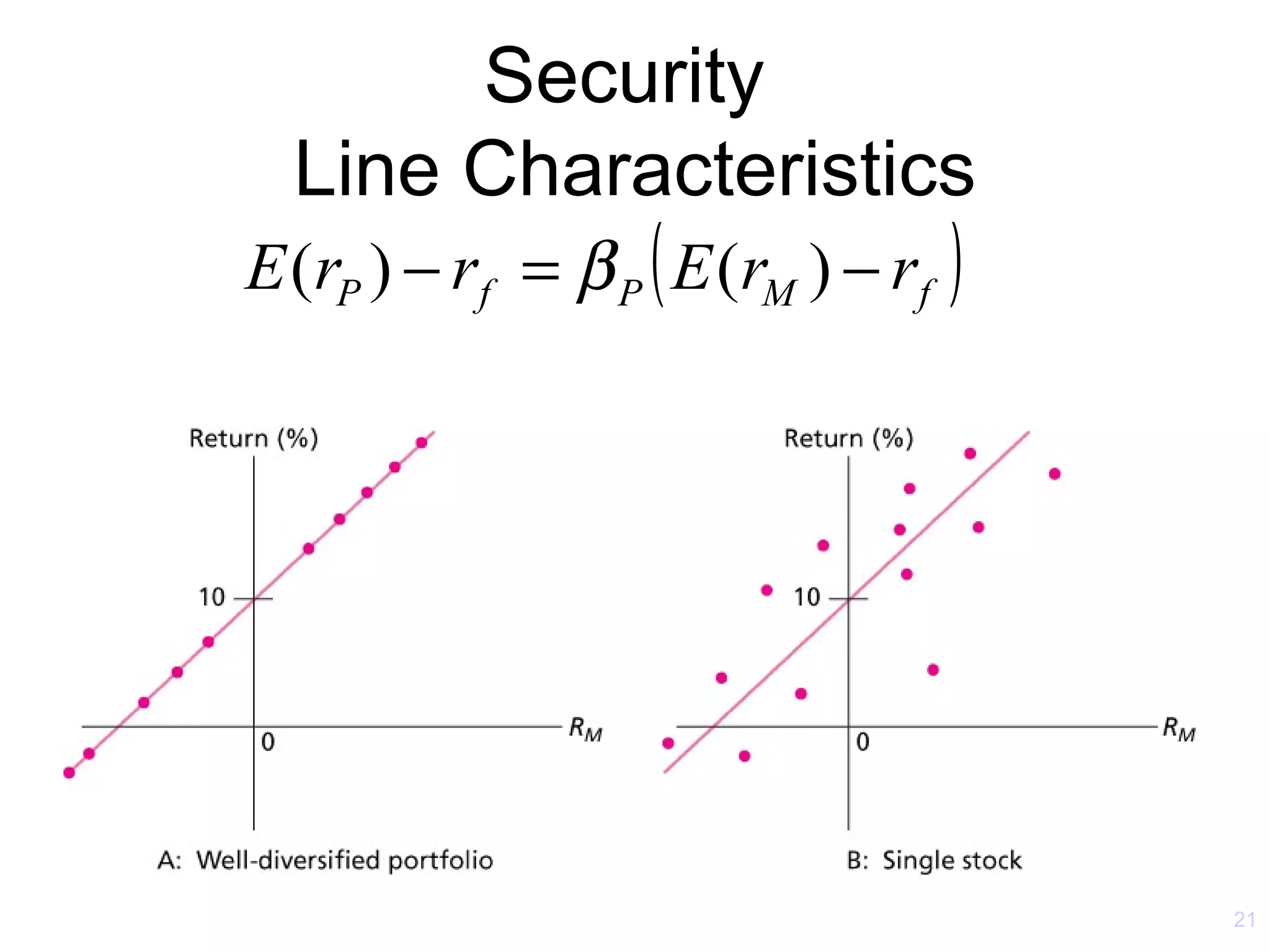
The document discusses the Capital Asset Pricing Model (CAPM) and Arbitrage Pricing Theory (APT). It outlines the key assumptions and results of CAPM, including that all investors hold the market portfolio and the security market line relates individual security risk premiums to market risk premiums through beta. It also discusses limitations of CAPM and how multifactor models like Fama-French can better describe returns. Finally, it explains how APT allows for arbitrage opportunities if mispriced portfolios exist and its relationship to CAPM.

1. Capital Asset Pricing and
Arbitrage Pricing Theory
Prof. Karim Mimouni
1

2. Capital Asset Pricing Model
(CAPM)
2

3. Assumptions
• Individual investors are price takers
• Single-period investment horizon
• Investments are limited to traded financial
assets
• No taxes, and transaction costs
3

4. Assumptions (cont.)
• Information is costless and available to all
investors
• Homogeneous expectations
4

5. Resulting Equilibrium
Conditions
• All investors will hold the same portfolio
for risky assets – market portfolio
• Market portfolio contains all securities
and the proportion of each security is its
market value as a percentage of total
market value
5

6. The Efficient Frontier and the
Capital Market Line
6

7. Slope and Market Risk Premium
M = Market portfolio
rf = Risk free rate
E(rM) - rf = Market risk premium
E(rM) - rf = Market price of risk
σM
= Slope of the CML
7

8. Expected Return and Risk
on Individual Securities
E (ri ) − rf = β i ( E (rM ) − rf )
M = Market portfolio
rf = Risk free rate
E(ri) - rf = Risk premium on security i
E(rM) - rf = Market risk premium
8

9. The Security Market Line and
Positive Alpha Stock
9

10. • Determine the equation of the SML and plot it
when:
( E (r
M ) − rf ) = 0.08
and
rf = 0.03
10

11. Application
• You are in an economy where Rf=9%,
E(Rm)=20%.
• Determine the equation of the SML line in
this economy.
• A stock has a beta=1.5. Determine the
required rate of return. Give your
recommendation when you think its
expected return will be 22%.
• Do the same analysis when beta=-0.5 and
investor expect the return to be 7% 11

12. Estimating the Index Model
• Using historical data on T-bills, S&P 500
and individual securities
• Regress risk premiums for individual
stocks against the risk premiums for the
S&P 500
• Slope is the beta for the individual stock
12

13. Characteristic Line for GM
13

14. Security Characteristic
Line for GM: Summary Output
14

15. Multifactor Models
15

16. • Limitations for CAPM
• Market Portfolio is not directly observable
• Research shows that other factors affect
returns
16

17. Fama French Research
• Returns are related to factors other than market
returns
• Size
• Book value relative to market value
• Three factor model better describes returns
• Example : GM
E (rGM ) − r f = β GM , M ( E (rM ) − rf ) + β GM ,SMB ( E (rSMB ) − rf ) + β GM , HML ( E (rHML ) − rf )
17

18. Regression Statistics for the Single-
index and FF Three-factor Model
18

19. Arbitrage Pricing Theory
19

20. • Arbitrage - arises if an investor can
construct a zero beta investment portfolio
with a return greater than the risk-free rate
• If two portfolios are mispriced, the investor
could buy the low-priced portfolio and sell
the high-priced portfolio
• In efficient markets, profitable arbitrage
opportunities will quickly disappear
20

21. Security
Line Characteristics
E (rP ) − rf = β P ( E (rM ) − rf )
21

22. APT and CAPM Compared
• APT applies to well diversified portfolios and not
necessarily to individual stocks
• With APT it is possible for some individual stocks
to be mispriced - not lie on the SML
• APT is more general in that it gets to an
expected return and beta relationship without the
assumption of the market portfolio
• APT can be extended to multifactor models
22