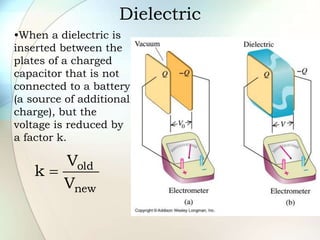
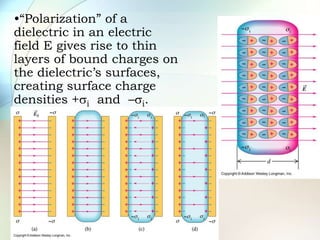
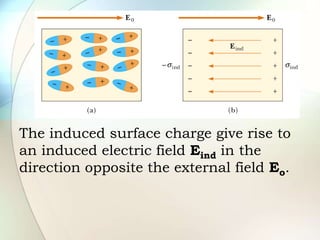
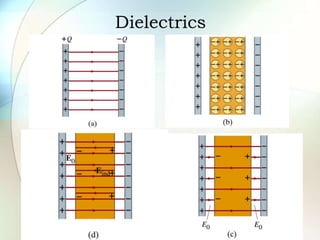
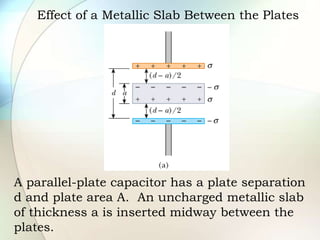
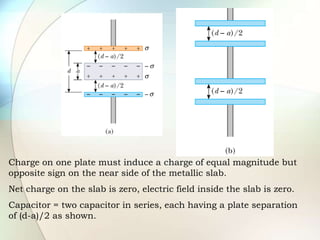
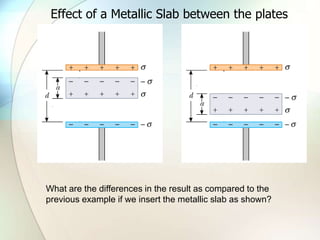
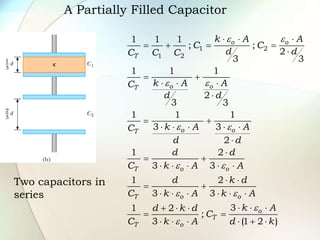
A dielectric is a nonconducting material inserted between the plates of a capacitor that increases the capacitor's ability to store an electric charge. When a dielectric is used, it increases the capacitance by a factor called the dielectric constant. The dielectric reduces the electric field strength inside itself and increases the breakdown voltage of the capacitor. Different dielectric materials have different dielectric constants depending on how easily their molecules can be polarized in an external electric field.

1. Capacitors with
Dielectrics
AP Physics C
Montwood High School
R. Casao

2. Dielectric
• A dielectric is a nonconducting material
inserted between the plates of a
capacitor.
• A dielectric increases the ability of a
capacitor to store energy.
• If the dielectric completely fills the space
between the plates, the capacitance
increases by a factor k, called the
dielectric constant.
d
A
ε
k
C o 



3. Dielectric
•When a dielectric is
inserted between the
plates of a charged
capacitor that is not
connected to a battery
(a source of additional
charge), but the
voltage is reduced by
a factor k.
new
old
V
V
k 

4. Dielectric
• Since the charge Q on the capacitor does not
change, then the capacitance must change
with the changing voltage so that the charge
remains constant.
• The capacitance increases by a factor k when
the dielectric completely fills the space between
the plates.
• The dielectric constant is a measure of the
degree of dipole alignment in the material.
old
new
C
C
k 

5. •From the equation for capacitance
the capacitance can be increased by decreasing
the distance d between the plates.
•The value of d is limited by the electrical
discharge that could occur through the
dielectric medium separating the plates.
•For any separation d, the maximum voltage
that can be applied across the capacitor plates
without causing a discharge depends on the
dielectric strength of the dielectric.
d
A
ε
k
C o 



6. •In other words, the
maximum electric field the
dielectric material can
withstand without allowing
a transfer of charge
between the plates is the
dielectric strength.
•If the electric field
strength in the dielectric
exceeds the dielectric
strength, the insulating
properties will break down
and the dielectric material
begins to conduct. This is
called dielectric
breakdown.
d
V
)
E
(
ds dielectric 


7. •“Polarization” of a
dielectric in an electric
field E gives rise to thin
layers of bound charges on
the dielectric’s surfaces,
creating surface charge
densities +si and –si.

8. An Atomic Description of Dielectrics
(a)Polar molecules are randomly oriented in
the absence of an external electric field.
(b)When an external field is applied (to the
right as shown), the molecules partially
align with the field; the dielectric is now
polarized.

9. (a) When a dielectric is polarized, the dipole moments of
the molecules in the dielectric are partially aligned with
the external field Eo. (b) This polarization causes an
induced charge on the opposite side. This separation of
charge results in a reduction in the net electric field
within the dielectric.
The net effect on the dielectric is the formation of an
induced positive surface charge density sind on the right
face and an equal negative surface charge density –sind
on the left face.

10. The induced surface charge give rise to
an induced electric field Eind in the
direction opposite the external field Eo.

11. What is the Magnitude of the Induced Charge Density?
Note that the induced
charge density on the
dielectric is less than the
charge density on the
plates.
For parallel plate capacitor,
External field Eo = s/eo
Induced Field Eind = sind/eo
and E = Eo/k = s/k·eo
Substitute into E = Eo - Eind gives
;
1
ind ind
o o o o o o
o o
ind
o o
ind
k k
k k
k k
k k k
s s
s s s s
e e e e e e
e s e s s
s s
e e
s s
s s
   
 
 
   

 
 
    
 

12. Dielectrics

13. • The net electric field in the dielectric is
given by: E = Eo - Einduced
• The dielectric provides these advantages:
• Increases the capacitance of the capacitor.
• Increases the maximum operating voltage of
a capacitor.
• May provide mechanical support between the
conducting plates.
new
old
E
E
k 



14. Effect of the Dielectric Constant
o
dielectric
E
E
k
 o
dielectric
E
E d d
k
  
o
dielectric
V
V
k

Potential difference with a dielectric
is less than the potential difference
across free space
o
o
Q Q
C k k C
V V
     Results in a higher capacitance.
Allows more charge to be stored before breakdown
voltage.

15. Effect of the Dielectric Constant
Parallel Plate Capacitor
o o
o o
A k A
C C k C
d d
e  e 
    
o
k
e  e
A
C
d
e

Material permittivity measures
degree to which the material
permits induced dipoles
to align with an external field.
2 2 2
o 0 0
1 1 1
u E u k E E
2 2 2
 e     e   e
Example modifications
using permittivity

16. •The energy of the capacitor is
lowered when a dielectric is
inserted between the plates.
Work is done on the dielectric.
•A force must act on the
dielectric which pulls it into the
capacitor.
•The nonuniform electric field
near the edges of a parallel plate
capacitor exerts this force.
•The horizontal component of
the electric field acts on the
induced charges on the surface
of the dielectric, producing a
horizontal force directed into the
capacitor.

17. • Place a dielectric material
between capacitor plates:
• A charge of -13 is on the right
negative plate of the capacitor.
• A charge of +7 is on the right
positive portion of the dielectric.
• The battery sees -13 + 7 = -6
(less total charge on the negative
capacitor plate).
• To compensate for the absence of
charge, the battery sends more
charge to the negative capacitor
plate to restore the -13 charge.
• This is how a dielectric allows for
more charge to be stored on the
capacitor plates.

18. Effect of a Metallic Slab Between the Plates
A parallel-plate capacitor has a plate separation
d and plate area A. An uncharged metallic slab
of thickness a is inserted midway between the
plates.

19. Charge on one plate must induce a charge of equal magnitude but
opposite sign on the near side of the metallic slab.
Net charge on the slab is zero, electric field inside the slab is zero.
Capacitor = two capacitor in series, each having a plate separation
of (d-a)/2 as shown.

20.    
 
1 2
1 1 1 1 1 1
;
2 2
1 2 1 2 1 1
; ;
2
2
1
;
o o
T T
o o o
T T T
o
T
T o
A A
C C C C
d a d a
A A A
C C C
d a d a d a
A
d a
C
C A d a
e e
e e e
e
e
   
 
 
  
   
  


 
 

21. Effect of a Metallic Slab between the plates
What are the differences in the result as compared to the
previous example if we insert the metallic slab as shown?

22. A Partially Filled Capacitor
A parallel-plate capacitor with a plate separation d has
a capacitance Co in the absence of a dielectric. What is
the capacitance when a slab of dielectric material of
dielectric constant k and thickness d/3 is inserted
between the plates as shown.

23. A Partially Filled Capacitor
Two capacitors in
series
1 2
1 2
1 1 1
; ;
2
3 3
1 1 1
2
3 3
1 1 1
3 3
2
1 2
3 3
1 2
3 3
3
1 2
;
3 (1 2 )
o o
T
o o
T
o o
T
T o o
T o o
o
T
T o
k A A
C C
d d
C C C
k A A
C
d d
k A A
C
d d
d d
C k A A
d k d
C k A k A
k A
d k d
C
C k A d k
e e
e e
e e
e e
e e
e
e
  
   

 
  

 
    


 
    
 
 
     
  
  
 
     

24. Two Dielectric Slabs
• Consider a parallel-plate
capacitor that has the space
between the plates filled with
two dielectric slabs, one with
constant k1 and one with
constant k2.
• The thickness of each slab is
the same as the plate
separation d and each slab
fills half the volume between
the plates.
• The two different dielectric
slabs represent two capacitors
in parallel with a plate area
A/2.

25. Two Dielectric Slabs
1 2
2
1
1 2
1 2
2 2
2
( )
2
T
o
o
T
o o
T
o
T
C C C
k A
k A
C
d d
k A k A
C
d
A k k
C
d
e
e
e e
e
 
 
 
 
 
    


  



26. Charge Storage Warning
• Capacitors can store a charge for a long time
after the power to them has been turned off.
This charge can be dangerous.
• A large electrolytic capacitor charged to only
5 V or 10 V can melt the tip of a screwdriver
placed across its terminal.
• High voltage capacitors like those in TV’s and
photoflash units can store a lethal charge.
• Technicians ground themselves to avoid electric
shock.