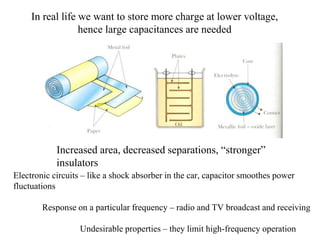
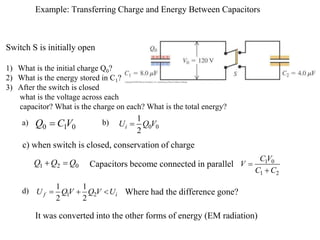
1) Dielectrics increase the capacitance of a capacitor by introducing polarizable molecules between the plates that can be oriented by an applied electric field. This leads to an increased charge storage capacity and a lower operating voltage. 2) The dielectric constant is a property of the material that quantifies its ability to increase capacitance. It is defined as the ratio of the capacitance with a dielectric to the capacitance without. 3) Dielectrics break down at a certain maximum electric field strength, above which the material can no longer maintain its insulating properties and will conduct electricity between the plates.

1. 22ECR224 VARUN.S
DIELECTRIC
CONSTANT

2. Energy Storage in Capacitors
Electric Field Energy
Electric potential energy stored = amount of work done to charge the capacitor
i.e. to separate charges and place them onto the opposite plates
Q
V
C

2
0 0
2 2
Total work ( )
2
1
Stored energy
2 2 2
Q Q
q Q
W V q dq dq
C C
Q CV
U QV
C
  
  
 
Charged capacitor – analog to stretched/compressed spring
Capacitor has the ability to hold both charge and energy
To transfer charge dq between
conductors, work dW=Vdq
Density of energy (energy/volume)
Energy is conserved in the E-field

3. In real life we want to store more charge at lower voltage,
hence large capacitances are needed
Increased area, decreased separations, “stronger”
insulators
Electronic circuits – like a shock absorber in the car, capacitor smoothes power
fluctuations
Response on a particular frequency – radio and TV broadcast and receiving
Undesirable properties – they limit high-frequency operation

4. Example: Transferring Charge and Energy Between Capacitors
Switch S is initially open
1) What is the initial charge Q0?
2) What is the energy stored in C1?
3) After the switch is closed
what is the voltage across each
capacitor? What is the charge on each? What is the total energy?
a) 0 1 0
Q C V
 0 0
1
2
i
U Q V

b)
c) when switch is closed, conservation of charge
1 2 0
Q Q Q
  Capacitors become connected in parallel 1 0
1 2
C V
V
C C


d) 1 2
1 1
2 2
f i
U QV Q V U
   Where had the difference gone?
It was converted into the other forms of energy (EM radiation)

5. Definitions
• Dielectric—an insulating material placed between plates of a
capacitor to increase capacitance.
• Dielectric constant—a dimensionless factor  that determines
how much the capacitance is increased by a dielectric. It is a
property of the dielectric and varies from one material to another.
• Breakdown potential—maximum potential difference before
sparking
• Dielectric strength—maximum E field before dielectric breaks
down and acts as a conductor between the plates (sparks)

6. Most capacitors have a non-conductive material (dielectric) between the conducting
plates. That is used to increase the capacitance and potential across the plates.
Dielectrics have no free charges and they do not conduct electricity
Faraday first established this
behavior

7. Capacitors with Dielectrics
• Advantages of a dielectric include:
1. Increase capacitance
2. Increase in the maximum operating voltage. Since dielectric
strength for a dielectric is greater than the dielectric strength
for air
3. Possible mechanical support between the plates which
decreases d and increases C.
• To get the expression for anything in the presence of a
dielectric you replace o with o
air
di
air
di V
V
E
E 


 



 max
max
max
max

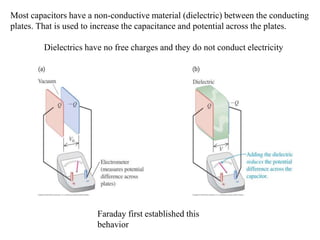
8. Field inside the capacitor became smaller – why?
There are polarization (induced)
charges
– Dielectrics get polarized
We know what happens to the conductor in the electric field
Field inside the conductor E=0
outside field did not change
Potential difference (which is the
integral of field) is, however, smaller.
( )
o
V d b


  0
[1 / ]
A
C
d b d




9. Properties of Dielectrics
0
E
E
K

Redistribution of charge – called polarization
We assume that the induced charge is directly
proportional to the E-field in the material
0
C
K
C
 dielectric constant of a material
0
V
V
K

when Q is kept constant
In dielectrics, induced charges do not exactly
compensate charges on the capacitance plates

10. 0
0 0
; i
E E
 

 

 
1
1
i
K
 
 
 
 
 
Induced charge density
0
K
 
 Permittivity of the dielectric material
E


 E-field, expressed through charge density  on the conductor plates
(not the density of induced charges) and permittivity of the dielectric
 (effect of induced charges is included here)
2
1
2
u E

 Electric field density in the dielectric
Example: A capacitor with and without dielectric
Area A=2000 cm2
d=1 cm; V0 = 3kV;
After dielectric is inserted, voltage V=1kV
Find; a) original C0 ; b) Q0 ; c) C d) K e) E-field

11. Dielectric Breakdown
Dielectric strength is the maximum electric field
the insulator can sustain before breaking down
Plexiglas breakdown

12. Molecular Model of Induced Charge
Electronic polarization of nonpolar molecules
tom)
molecule/a
a
of
lity
polarizabi
the
is
(
:
field
in the
moment
dipole
finite
acquire
but they
field
electric
applied
the
of
absence
in the
0
molecules
nonpolar
For
ng
nonvanishi
be
may
moment
dipole
But
0
charge
Total
0

 E
d
E
d
r
d







i
i
i
i
i
q
q
Q

13. In the electric field more molecular dipoles are oriented
along the field
Electronic polarization of polar molecules

14. Polarizability of an Atom

- separation of proton and electron cloud in the applied
electric field
P- dipole moment per unit volume, N – concentration of atoms
0
When per unit volume, this dipole moment is called
polarization vector Nq 
 
P δ E
ind
0
fre
Property of the material: Dielectric susceptibility
Polarization charges induced on the surface:
For small displacements: P~E; P=
The field inside the dielectric is :
n
N
P
E
E
 




  

P n
reduced
e ind 0 free
0 0
ind free
1
1 ; ( )
E
K K
K
K
K
 
 
  

 

  

15. Gauss’s Law in Dielectrics
0
( )
i A
EA
 



1
1
i
K
 
 
 
 
 
0
A
KEA



0
free
Q
K E d A

 

 Gauss’s Law inDielectrics

16. Forces Acting on Dielectrics
More charge here
We can either compute force directly
(which is quite cumbersome), or use
relationship between force and energy
F U
 
Considering parallel-plate capacitor
2
2
CV
U 
Force acting on the capacitor, is pointed inside,
hence, E-field work done is positive and U - decreases
2
2
x
U V C
F
x x
 
  
 
x – insertion length
Two capacitors in parallel
0 0
1 2 w( ) w
K
C C C L x x
d d
 
     w – width of the plates
2
0w
( 1)
2
x
V
F K
d

  constant force

17. Thank you