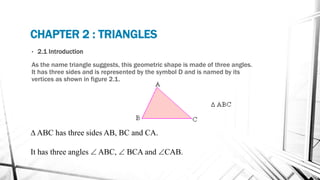
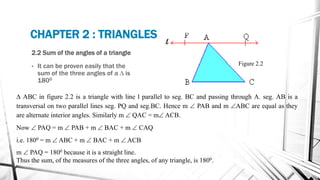
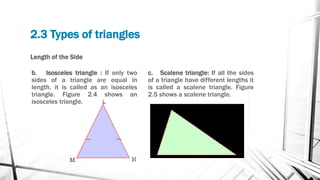
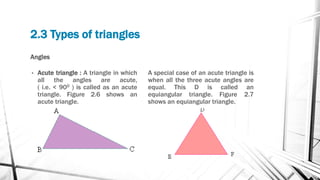
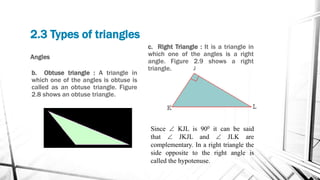
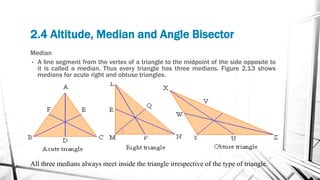
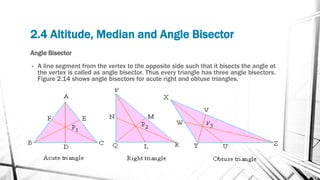
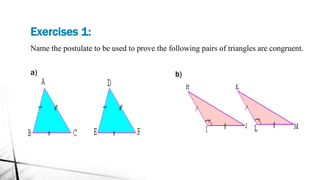
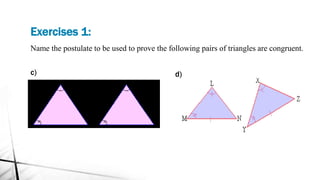
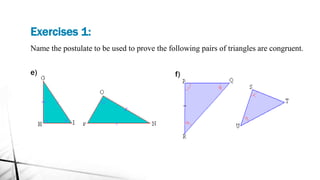
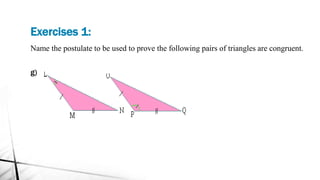
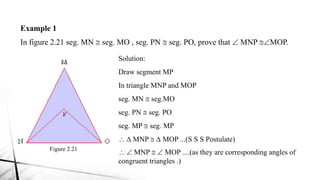
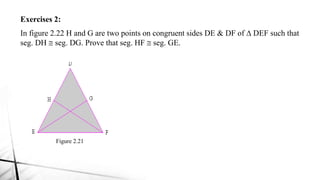
Chapter 2 discusses triangles, covering their properties, classifications, and congruence criteria. It explains the sum of angles in a triangle, types of triangles categorized by side lengths and angles, as well as key concepts such as altitude, median, and angle bisector. The chapter concludes with the conditions under which triangles are considered congruent.

1. Chapter 2
Triangles

2. CHAPTER 2 : TRIANGLES
2.1 Introduction
2.2 Sum of the angles of a triangle
2.3 Types of triangles
2.4 Altitude, Median and Angle Bisector
2.5 Congruence of triangles
2.6 Sides opposite congruent angles

3. CHAPTER 2 : TRIANGLES
• 2.1 Introduction
As the name triangle suggests, this geometric shape is made of three angles.
It has three sides and is represented by the symbol D and is named by its
vertices as shown in figure 2.1.
D ABC has three sides AB, BC and CA.
It has three angles  ABC,  BCA and CAB.

4. 2.2 Sum of the angles of a triangle
• It can be proven easily that the
sum of the three angles of a D is
1800
CHAPTER 2 : TRIANGLES
Figure 2.2
D ABC in figure 2.2 is a triangle with line l parallel to seg. BC and passing through A. seg. AB is a
transversal on two parallel lines seg. PQ and seg.BC. Hence m  PAB and m ABC are equal as they
are alternate interior angles. Similarly m  QAC = m ACB.
Now  PAQ = m  PAB + m  BAC + m  CAQ
i.e. 1800 = m  ABC + m  BAC + m  ACB
m  PAQ = 1800 because it is a straight line.
Thus the sum, of the measures of the three angles, of any triangle, is 1800.

5. 2.3 Types of triangles
• Triangles are classified into
various types, using two different
parameters - the lengths of their
sides and the measure of their
angles.
• Length of the Side
a. Equilateral triangle : If the lengths
of all three sides of the triangle are
equal, then it is called an equilateral
triangle. Figure 2.3 shows an
equilateral triangle.
Figure 2.3

6. Length of the Side
b. Isosceles triangle : If only two
sides of a triangle are equal in
length, it is called as an isosceles
triangle. Figure 2.4 shows an
isosceles triangle.
c. Scalene triangle: If all the sides
of a triangle have different lengths it
is called a scalene triangle. Figure
2.5 shows a scalene triangle.
2.3 Types of triangles

7. Angles
• Acute triangle : A triangle in which
all the angles are acute,
( i.e. < 900 ) is called as an acute
triangle. Figure 2.6 shows an
acute triangle.
A special case of an acute triangle is
when all the three acute angles are
equal. This D is called an
equiangular triangle. Figure 2.7
shows an equiangular triangle.
2.3 Types of triangles

8. 2.3 Types of triangles
Angles
b. Obtuse triangle : A triangle in
which one of the angles is obtuse is
called as an obtuse triangle. Figure
2.8 shows an obtuse triangle.
c. Right Triangle : It is a triangle in
which one of the angles is a right
angle. Figure 2.9 shows a right
triangle.
Since  KJL is 900 it can be said
that  JKJL and  JLK are
complementary. In a right triangle the
side opposite to the right angle is
called the hypotenuse.

9. 2.4 Altitude, Median and Angle Bisector
Altitude
• An altitude is a perpendicular
dropped from one vertex to the
side ( or its extension ) opposite to
the vertex. It measures the
distance between the vertex and
the line which is the opposite side.
Since every triangle has three
vertices it has three altitudes.
a. Altitudes of an acute triangle :
For an acute triangle figure 2.10 all the
altitudes are present in the triangle.

10. 2.4 Altitude, Median and Angle Bisector
b. Altitudes for a right triangle : • For a right triangle two of the
altitudes lie on the sides of the
triangle, seg. AB is an altitude
from A on to seg. BC and seg. CB
is an altitude from C on to seg.AB.
Both of them are on the sides of
the triangle. The third altitude is
seg. BD i.e.from B on to AC. The
intersection point of seg. AB, seg.
BC and seg. BD is B. Thus for a
right triangle the three altitudes
intersect at the vertex of the right
angle.
Figure 2.11

11. 2.4 Altitude, Median and Angle Bisector
c. Altitudes for an obtuse triangle :
• D ABC is an obtuse triangle.
Altitude from A meets line
containing seg.BC at D. Therefore
seg. AD is the altitude. Similarly
seg.CE is altitude on to AB and BF
is the altitude on to seg. AC. Of the
three altitudes, only one is present
inside the triangle. The other two
are on the extensions of line
containing the opposite side.
These three altitudes meet at
point P which is outside the
triangle.
Figure 2.12

12. 2.4 Altitude, Median and Angle Bisector
Median
• A line segment from the vertex of a triangle to the midpoint of the side opposite to
it is called a median. Thus every triangle has three medians. Figure 2.13 shows
medians for acute right and obtuse triangles.
All three medians always meet inside the triangle irrespective of the type of triangle.

13. 2.4 Altitude, Median and Angle Bisector
Angle Bisector
• A line segment from the vertex to the opposite side such that it bisects the angle at
the vertex is called as angle bisector. Thus every triangle has three angle bisectors.
Figure 2.14 shows angle bisectors for acute right and obtuse triangles.

14. 2.5 Congruence of triangles
Two triangles are said to be congruent, if all the corresponding parts are
equal. The symbol used for denoting congruence is @ and D PQR @ D STU
implies that
and also
i.e. corresponding angles and corresponding sides are equal.

15. 2.5 Congruence of triangles
S S S Postulate
If all the sides of one triangle are congruent to the corresponding sides of another
triangle then the triangles are congruent (figure 2.15 ).
seg. AB = seg. PQ , seg. BC = seg. QR
and
seg. CA = seg. RP
D ABC @ D PQR by S S S.

16. 2.5 Congruence of triangles
S A S Postulate
If the two sides and the angle included in one triangle are congruent to the
corresponding two sides and the angle included in another triangle then the
two triangles are congruent (figure 2.16).
seg. AB = seg. PQ , seg. BC = seg. QR
and
m  ABC = m  PQR
D ABC @ D PQR by S A S postulate.

17. 2.5 Congruence of triangles
A S A Postulate
If two angles of one triangle and the side they include are congruent to the
corresponding angles and side of another triangle the two triangles are congruent
(figure 2.17 ).
m  B + m  R m  L = m  P and
seg. BC = seg. RP
D ABC @ D QRP by A S A postulate.

18. 2.5 Congruence of triangles
AA S Postulate
If two angles of a triangle and a side not included by them are congruent to the
corresponding angles and side of another triangle the two triangles are
congruent (figure 2.18)
m  A = m  P m  B = m  Q and
AC = PR
D ABC @ D PQR by AA S.

19. 2.5 Congruence of triangles
H S Postulate
This postulate is applicable only to right triangles. If the hypotenuse and any one
side of a right triangle are congruent to the hypotenuse and the corresponding side
of another right triangle then the two triangles are congruent (figure 2.19).
Then hypotenuse AC = hypotenuse PR
Side AB = Side PQ
D ABC @ D PQR by HS postulate.

20. Exercises 1:
Name the postulate to be used to prove the following pairs of triangles are congruent.
a) b)

21. Exercises 1:
Name the postulate to be used to prove the following pairs of triangles are congruent.
c) d)

22. Exercises 1:
Name the postulate to be used to prove the following pairs of triangles are congruent.
e) f)

23. Exercises 1:
Name the postulate to be used to prove the following pairs of triangles are congruent.
g)

24. Example 1
In figure 2.21 seg. MN @ seg. MO , seg. PN @ seg. PO, prove that  MNP @MOP.
Figure 2.21
Solution:
Draw segment MP
In triangle MNP and MOP
seg. MN @ seg.MO
seg. PN @ seg. PO
seg. MP @ seg. MP
D MNP @ D MOP ...(S S S Postulate)
 MNP @  MOP ....(as they are corresponding angles of
congruent triangles .)

25. Figure 2.21
Exercises 2:
In figure 2.22 H and G are two points on congruent sides DE & DF of D DEF such that
seg. DH @ seg. DG. Prove that seg. HF @ seg. GE.

26. 2.6 Sides opposite congruent angles
Theorem : If two sides of a triangle are equal, then the angles opposite
them are also equal. This can be proven as follows :
Consider a D ABC where AB = AC ( figure 2.23 ).
Figure 2.23
Proof : To prove m  B = m  C drop a median from A to BC at point P.
Since AP is the median, BP = CP.
In D ABP and D ACP
seg. AB @ seg. AC( given )
seg. BP @ seg. CP( P is midpoint )
seg. AP @ seg. AP( same line )
Therefore the two triangles are congruent by SSS postulate.
D ABP @ D ACP
m  B = m  C as they are corresponding angles of congruent triangles.

27. 2.6 Sides opposite congruent angles
Figure 2.24
The converse of this theorem is also true and can be proven quite easily.
Consider D ABC where m  B = m  C ( figure 2.24 )
To prove AB = AC drop an angle bisector AP on to BC.
Since AP is a bisector m  BAP = m  CAP
m  ABP = m  ACP ( given )
seg. AP @ seg. AP (same side )
D ABP @ D ACP by AAS postulate.
Therefore the corresponding sides are equal.
seg. AB = seg. AC
Conclusion :If the two angles of a triangle are equal, then the sides opposite to them
are also equal.

28.  end 