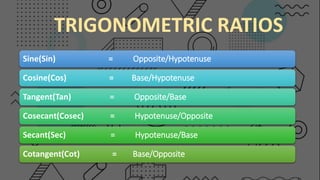
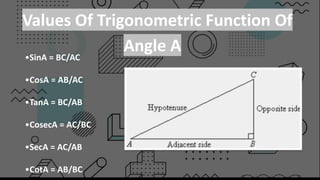
Trigonometry is a branch of mathematics that deals with triangles and uses ratios of sides to determine unknown angles or lengths. It defines trigonometric functions like sine, cosine, and tangent that relate the angles and sides of a right triangle. For example, the sine of an angle is equal to the ratio of the opposite side to the hypotenuse. Trigonometry has applications in fields like surveying, navigation, and physics that require calculating distances and heights.
This is a school standard presentation for class 10 students .
It will be very helpful to you all.
Hope you all like this .
And pass your exams with flying colors
It is a ppt on Trigonometry for th students of class 10 .
The basic concepts of trigonometry are provided here with examples Hope that that you like it .!! Thankyou ..!! :)
The data is present below the pictures so as to edit it as per your needs. I wanted to use good fonts and this was the only way i could do it as the fonts would not be available on your computer.
This is a school standard presentation for class 10 students .
It will be very helpful to you all.
Hope you all like this .
And pass your exams with flying colors
It is a ppt on Trigonometry for th students of class 10 .
The basic concepts of trigonometry are provided here with examples Hope that that you like it .!! Thankyou ..!! :)
The data is present below the pictures so as to edit it as per your needs. I wanted to use good fonts and this was the only way i could do it as the fonts would not be available on your computer.
this is a slide share on introduction of trigonometry this slide share includes every single information about the lesson trigonometry and this is best for class 10
Power point presentation based on trigonometry, easy to understand, for class XI, good for learning faster and easier, also could be understood by below class XI.
This lesson is the second of the series I am working on. It really should have come first, though. This lesson introduces trigonometry, detailing what it is, what is uses and a few important topics and formulas you'll find yourself using quite frequently.
Has everything needed for a CBSE Student to make up a project on Trigonometry. I hope this helps you all...
Topics:-
Intro, Information, Formulas, Summary and overview
this is a slide share on introduction of trigonometry this slide share includes every single information about the lesson trigonometry and this is best for class 10
Power point presentation based on trigonometry, easy to understand, for class XI, good for learning faster and easier, also could be understood by below class XI.
This lesson is the second of the series I am working on. It really should have come first, though. This lesson introduces trigonometry, detailing what it is, what is uses and a few important topics and formulas you'll find yourself using quite frequently.
Has everything needed for a CBSE Student to make up a project on Trigonometry. I hope this helps you all...
Topics:-
Intro, Information, Formulas, Summary and overview
Trigonometry Presentation For Class 10 StudentsAbhishek Yadav
Presentation on Trigonometry. A topic for class 10 Students. Has every topic covered for students wanting to make a presentation on Trigonometry. Hope this will help you...........
Operation “Blue Star” is the only event in the history of Independent India where the state went into war with its own people. Even after about 40 years it is not clear if it was culmination of states anger over people of the region, a political game of power or start of dictatorial chapter in the democratic setup.
The people of Punjab felt alienated from main stream due to denial of their just demands during a long democratic struggle since independence. As it happen all over the word, it led to militant struggle with great loss of lives of military, police and civilian personnel. Killing of Indira Gandhi and massacre of innocent Sikhs in Delhi and other India cities was also associated with this movement.
Welcome to TechSoup New Member Orientation and Q&A (May 2024).pdfTechSoup
In this webinar you will learn how your organization can access TechSoup's wide variety of product discount and donation programs. From hardware to software, we'll give you a tour of the tools available to help your nonprofit with productivity, collaboration, financial management, donor tracking, security, and more.
Embracing GenAI - A Strategic ImperativePeter Windle
Artificial Intelligence (AI) technologies such as Generative AI, Image Generators and Large Language Models have had a dramatic impact on teaching, learning and assessment over the past 18 months. The most immediate threat AI posed was to Academic Integrity with Higher Education Institutes (HEIs) focusing their efforts on combating the use of GenAI in assessment. Guidelines were developed for staff and students, policies put in place too. Innovative educators have forged paths in the use of Generative AI for teaching, learning and assessments leading to pockets of transformation springing up across HEIs, often with little or no top-down guidance, support or direction.
This Gasta posits a strategic approach to integrating AI into HEIs to prepare staff, students and the curriculum for an evolving world and workplace. We will highlight the advantages of working with these technologies beyond the realm of teaching, learning and assessment by considering prompt engineering skills, industry impact, curriculum changes, and the need for staff upskilling. In contrast, not engaging strategically with Generative AI poses risks, including falling behind peers, missed opportunities and failing to ensure our graduates remain employable. The rapid evolution of AI technologies necessitates a proactive and strategic approach if we are to remain relevant.
Palestine last event orientationfvgnh .pptxRaedMohamed3
An EFL lesson about the current events in Palestine. It is intended to be for intermediate students who wish to increase their listening skills through a short lesson in power point.
Instructions for Submissions thorugh G- Classroom.pptxJheel Barad
This presentation provides a briefing on how to upload submissions and documents in Google Classroom. It was prepared as part of an orientation for new Sainik School in-service teacher trainees. As a training officer, my goal is to ensure that you are comfortable and proficient with this essential tool for managing assignments and fostering student engagement.
Introduction to AI for Nonprofits with Tapp NetworkTechSoup
Dive into the world of AI! Experts Jon Hill and Tareq Monaur will guide you through AI's role in enhancing nonprofit websites and basic marketing strategies, making it easy to understand and apply.
Synthetic Fiber Construction in lab .pptxPavel ( NSTU)
Synthetic fiber production is a fascinating and complex field that blends chemistry, engineering, and environmental science. By understanding these aspects, students can gain a comprehensive view of synthetic fiber production, its impact on society and the environment, and the potential for future innovations. Synthetic fibers play a crucial role in modern society, impacting various aspects of daily life, industry, and the environment. ynthetic fibers are integral to modern life, offering a range of benefits from cost-effectiveness and versatility to innovative applications and performance characteristics. While they pose environmental challenges, ongoing research and development aim to create more sustainable and eco-friendly alternatives. Understanding the importance of synthetic fibers helps in appreciating their role in the economy, industry, and daily life, while also emphasizing the need for sustainable practices and innovation.
Biological screening of herbal drugs: Introduction and Need for
Phyto-Pharmacological Screening, New Strategies for evaluating
Natural Products, In vitro evaluation techniques for Antioxidants, Antimicrobial and Anticancer drugs. In vivo evaluation techniques
for Anti-inflammatory, Antiulcer, Anticancer, Wound healing, Antidiabetic, Hepatoprotective, Cardio protective, Diuretics and
Antifertility, Toxicity studies as per OECD guidelines
Unit 8 - Information and Communication Technology (Paper I).pdfThiyagu K
This slides describes the basic concepts of ICT, basics of Email, Emerging Technology and Digital Initiatives in Education. This presentations aligns with the UGC Paper I syllabus.
Macroeconomics- Movie Location
This will be used as part of your Personal Professional Portfolio once graded.
Objective:
Prepare a presentation or a paper using research, basic comparative analysis, data organization and application of economic information. You will make an informed assessment of an economic climate outside of the United States to accomplish an entertainment industry objective.
3. •The distances or heights can be found by using some mathematical techniques
, which come under a branch of mathematics called ‘trigonometry’.
•The word ‘trigonometry’ is derived from Greek words ‘tri’
(meaning three),’gon’(meaning sides) and metron(meaning measure)
•Trigonometry is the branch of mathematics which deals with
triangles, particularly triangles in a plane where one angle of the triangle is 90
degrees
Introduction
4. •A triangle in which one angle is equal to 90 is called right triangle.
•The side opposite to the right angle is known as hypotenuse. It is also
the longest side in a Right Angled Triangled.
•The other two sides are known as legs.
•AC is the hypotenuse
•AB and BC are the legs
Right Triangle
5. • In any right triangle, the area of the square whose side is the hypotenuse
is equal to the sum of areas of the squares whose sides are the two legs.
• In the figure AB2 = BC2 + AC2
• For Example:-
Pythagoras Theorem
