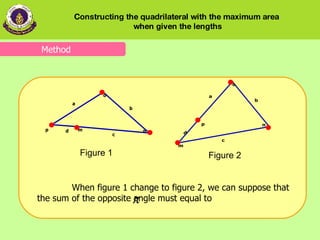
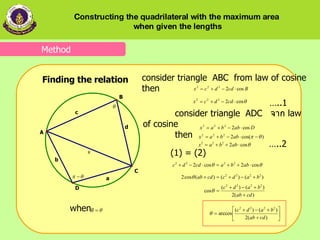
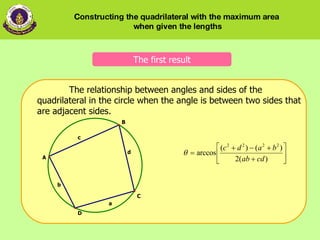
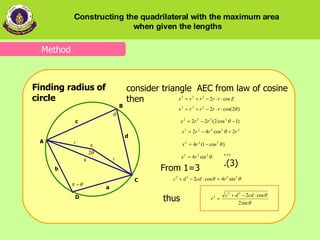
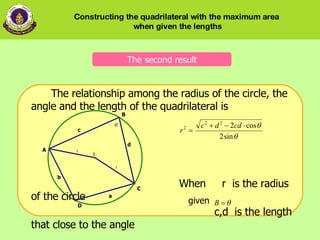
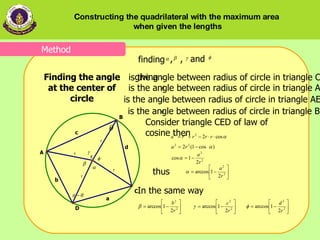
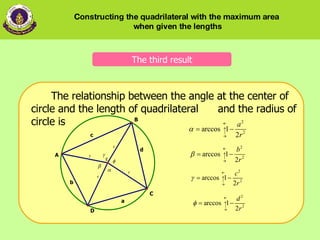
The document discusses constructing the quadrilateral with the maximum area given the lengths of its four sides. It presents five key results: 1) The relationship between angles and sides of the quadrilateral when constructed in a circle with the angle between two adjacent sides. 2) The relationship among the radius of the circle, the angle, and the lengths of sides close to the angle. 3) The relationship between the angle at the center of the circle and the length of sides and radius. 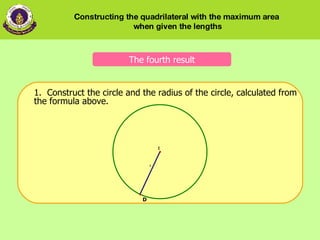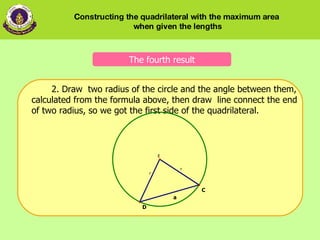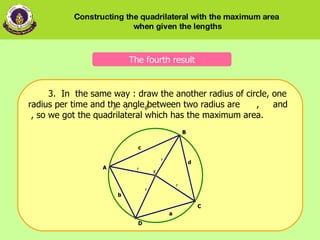4) How to construct the maximum area quadrilateral by drawing the sides in a circle based on calculated radii and angles. 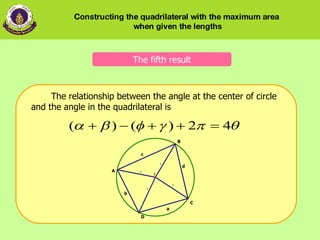5) The relationship between the angle at the center of the circle and the angles in the quadrilateral.

1. Krittika Poksawat N0.2 Class M.6/4 Tatcha Tratornpisuttikul N0.12 Class M.6/4 Worawoot Sumontra N0.23 Class M.6/4 Mahidol Wittayanusorn Constructing the quadrilateral with the maximum area when given the lengths

2. Adviser Miss Nongluck Arpasut Mr. Sunya Phumkumarn Constructing the quadrilateral with the maximum area when given the lengths

3. Introduction Currently, to find the area of any geometric figure is usually from any ready made figure. In another way, if the sides of figure are given then many geometric figures can be made. Our group will study how to construct maximal area figures especially in quadrilateral. The study is to examine that how the given four sides can be arranged and how to adjust the angles to construct a maximal area quadrilateral. Constructing the quadrilateral with the maximum area when given the lengths

4. Objective To study the arrangement of sides of the quadrilateral with the maximum area. To study the relation of angles and sides of the quadrilateral with the maximum area. 3. To use the Mathematics knowledge to solve the problem. Constructing the quadrilateral with the maximum area when given the lengths

5. that cos ( A+B) equal to 0 . So that Consider , the area of the quadrilateral Area = When given The area will be the maximum when Method is the smallest That is we must construct the quadrilateral in the circle. Constructing the quadrilateral with the maximum area when given the lengths

6. So that, we can find the maximum area. Area = When given Method Constructing the quadrilateral with the maximum area when given the lengths

7. Consider, the quadrilateral with the sum of the opposite angle equal to 180. Given the quadrilateral mnop with the sides, a,b,c,d . Method Constructing the quadrilateral with the maximum area when given the lengths

8. Figure 1 Figure 2 When figure 1 change to figure 2, we can suppose that the sum of the opposite angle must equal to Method Constructing the quadrilateral with the maximum area when given the lengths

9. Method 1.) Consider the order of four sides. We found that it can be 3! or 6 figures and the sum of length of three sides of quadrilateral must more than another one. Thus every quadrilaterals can construct 6 figures. 2.) Consider the order of four sides. We found that the 6 figures must have the same maximum area . The maximum area can calculate from the formula that is when Constructing the quadrilateral with the maximum area when given the lengths

10. consider triangle ADC จาก law of cosine then consider triangle ABC from law of cosine then … ..1 … ..2 (1) = (2) when Finding the relation Method Constructing the quadrilateral with the maximum area when given the lengths

11. consider triangle AEC from law of cosine then … .(3) thus From 1=3 Finding radius of circle Method Constructing the quadrilateral with the maximum area when given the lengths

12. finding , , and giving is the angle between radius of circle in triangle CED is the angle between radius of circle in triangle AED is the angle between radius of circle in triangle AEB is the angle between radius of circle in triangle BEC Consider triangle CED of law of cosine then thus In the same way Finding the angle at the center of circle Method Constructing the quadrilateral with the maximum area when given the lengths

13. consider then … .(1) (1)+(2) thus … .(2) Finding the relation of angles Method Constructing the quadrilateral with the maximum area when given the lengths

14. The relationship between angles and sides of the quadrilateral in the circle when the angle is between two sides that are adjacent sides. The first result Constructing the quadrilateral with the maximum area when given the lengths

15. The relationship among the radius of the circle, the angle and the length of the quadrilateral is When r is the radius of the circle c,d is the length that close to the angle given The second result Constructing the quadrilateral with the maximum area when given the lengths

16. The relationship between the angle at the center of circle and the length of quadrilateral and the radius of circle is The third result Constructing the quadrilateral with the maximum area when given the lengths

17. When we know the four lengths of quadrilateral, we can construct the quadrilateral which has the maximum areas by construct it in the circle and how to construct is here. The forth result Constructing the quadrilateral with the maximum area when given the lengths

18. 1. Construct the circle and the radius of the circle, calculated from the formula above. The fourth result Constructing the quadrilateral with the maximum area when given the lengths

19. 2 . Draw two radius of the circle and the angle between them, calculated from the formula above, then draw line connect the end of two radius, so we got the first side of the quadrilateral. The fourth result Constructing the quadrilateral with the maximum area when given the lengths

20. 3. In the same way : draw the another radius of circle, one radius per time and the angle between two radius are , and , so we got the quadrilateral which has the maximum area. The fourth result Constructing the quadrilateral with the maximum area when given the lengths

21. The relationship between the angle at the center of circle and the angle in the quadrilateral is The fifth result Constructing the quadrilateral with the maximum area when given the lengths