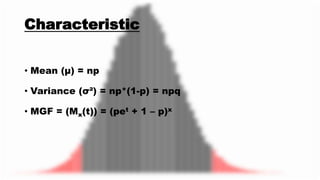
The document discusses the binomial distribution and its applications. It begins by explaining the origin of the binomial distribution, which was discovered by Jacob Bernoulli in the early 1700s. It then defines the binomial distribution as giving two possible results of an experiment with a fixed number of independent Bernoulli trials - success or failure. The key properties are outlined as having two outcomes, a fixed number of trials, constant probability of success/failure per trial, and independent trials. Applications mentioned include using it to model consumer behavior data from market research surveys, success/failure of medical drug trials, and quality control processes.

1. Binomial-
Distribution & It’s
Application
Group – 6
NAME Roll No.
Mayur Kasat MBA202224-090
Neelmani Singh MBA202224-098
Nishant Jha MBA202224-100
Palak Jain MBA202224-101
Rounak Rathi MBA202224-132

2. Origin
Binomial Distribution was discovered
by the Swiss mathematician Jacob
Bernoulli (1654-1705) in a proof,
published posthumously in 1713

3. What?
• The binomial distribution is the discrete probability
distribution that gives only two possible results in
an experiment, either Success or Failure.
• Consider a fixed number of mutually independent
Bernoulli trials where ‘p’ denotes the probability of
success. So a random variable called Bernoulli
random variable represents the total no. of success
in the ‘n’ independent Bernoulli trial. f(X) = P(X=x)
• P(X=x) = nCx px (1-p)n-x Or P(X=x) = nCx px (q)n-x
• X ~ Binomial(n,p) where; 0<p<1

4. Properties Of Binomial Distribution
• There are two possible outcomes: true or false,
success or failure, yes or no.
• There is ‘n’ number of independent trials or a fixed
number of n times repeated trials.
• The probability of success or failure remains the same
for each trial.
• Only the number of successes is calculated out of n
independent trials.
• Every trial is an independent trial, meaning the
outcome of one trial does not affect the outcome of
another.

5. Characteristic
• Mean (µ) = np
• Variance (σ²) = np*(1-p) = npq
• MGF = (Mx(t)) = (pet + 1 – p)x

6. Applications Of Binomial
Distribution

7. Market Research
• Businesses often conduct surveys to
gather data on consumer behavior or
preference.
• To estimate the proportion of consumers
who prefers certain products or
services.
• To model the probability of a consumer
responding to a campaign, given the
target audience size and success rate of
the movement.
• Probability of a certain no. of sales in a
fixed period based on historical data and
market trends

8. Medical Field
• Medical trials to determine the probability
of successes or failures in a given no. of
patients.
• For example, a drug company may test a
new drug on a group of 100 patients to
calculate a certain number of patients
responding to a drug.
• In Genetics, the distribution can be used to
model the distribution of genotypes in a
population. The probability of a particular
genotype is the probability of success.

9. Quality Control

10. Quality Control

11. Quality Control

12. THANK - YOU