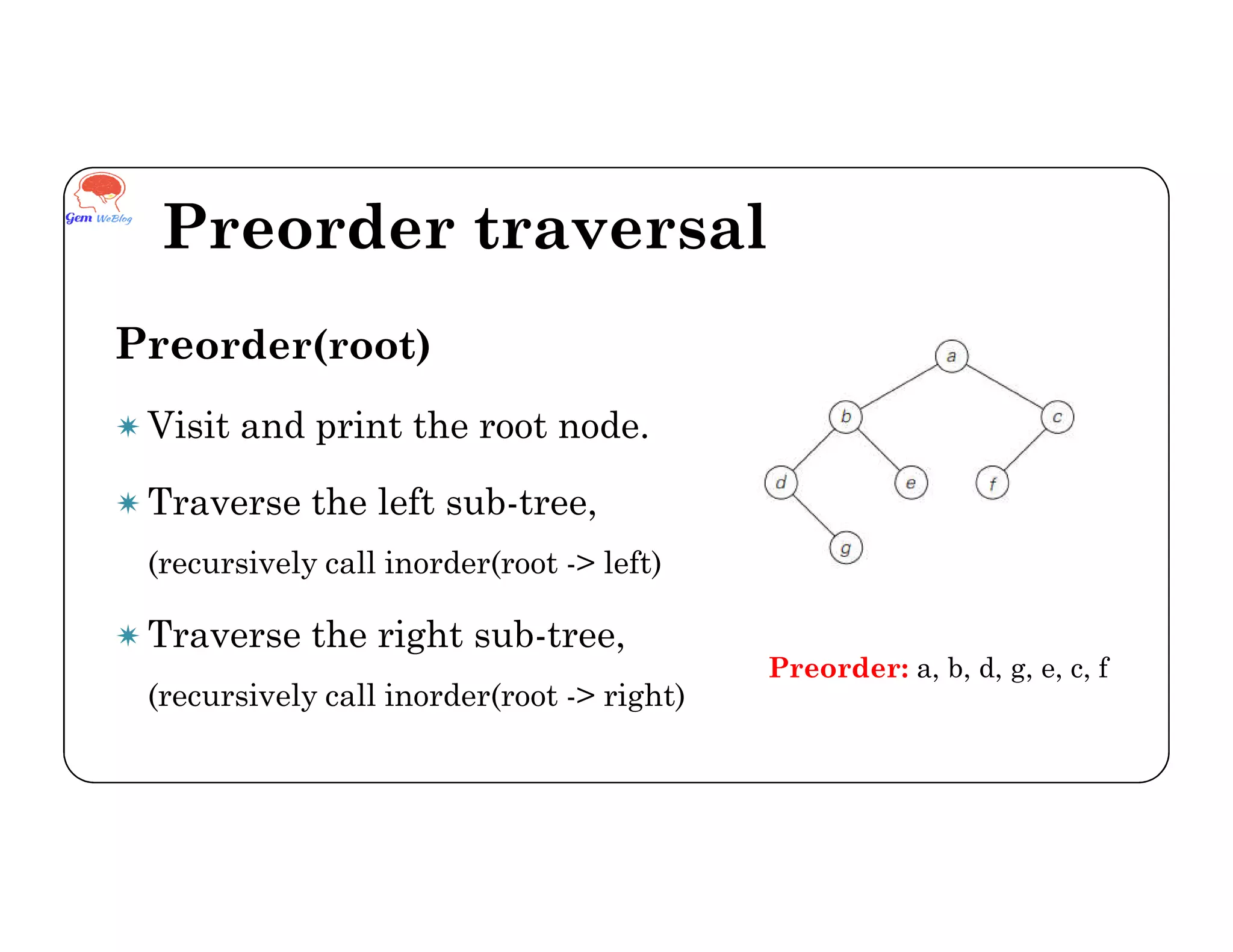
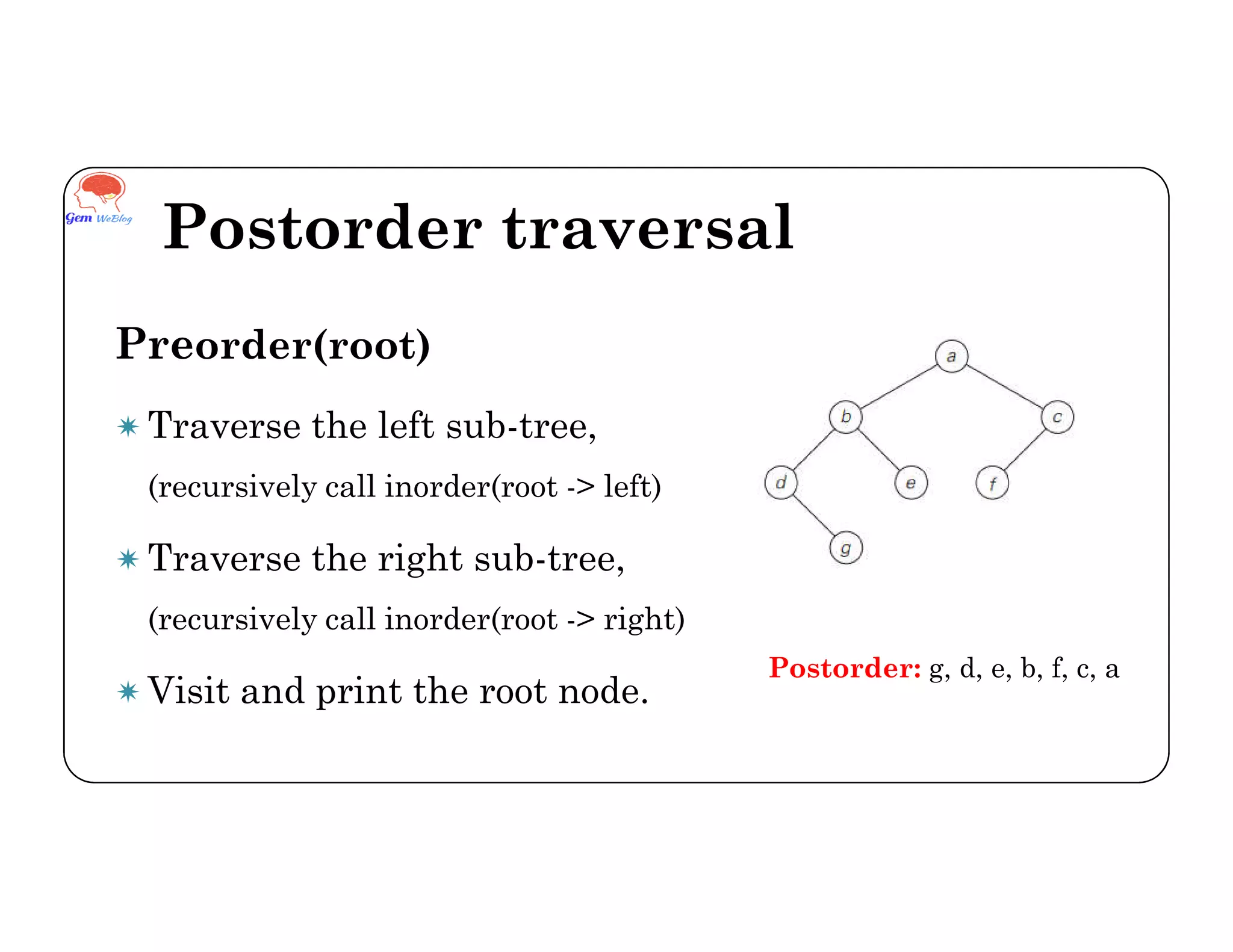
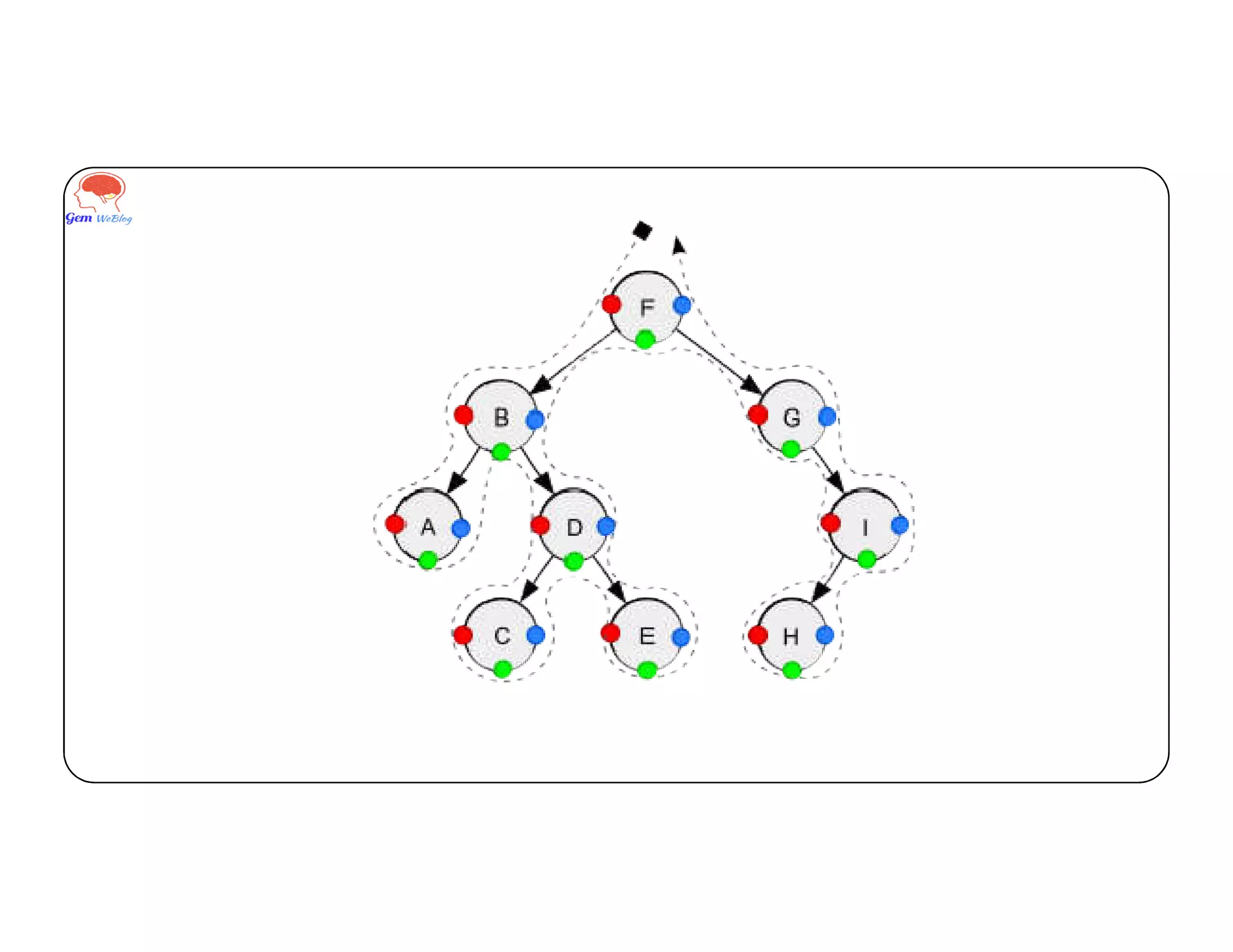
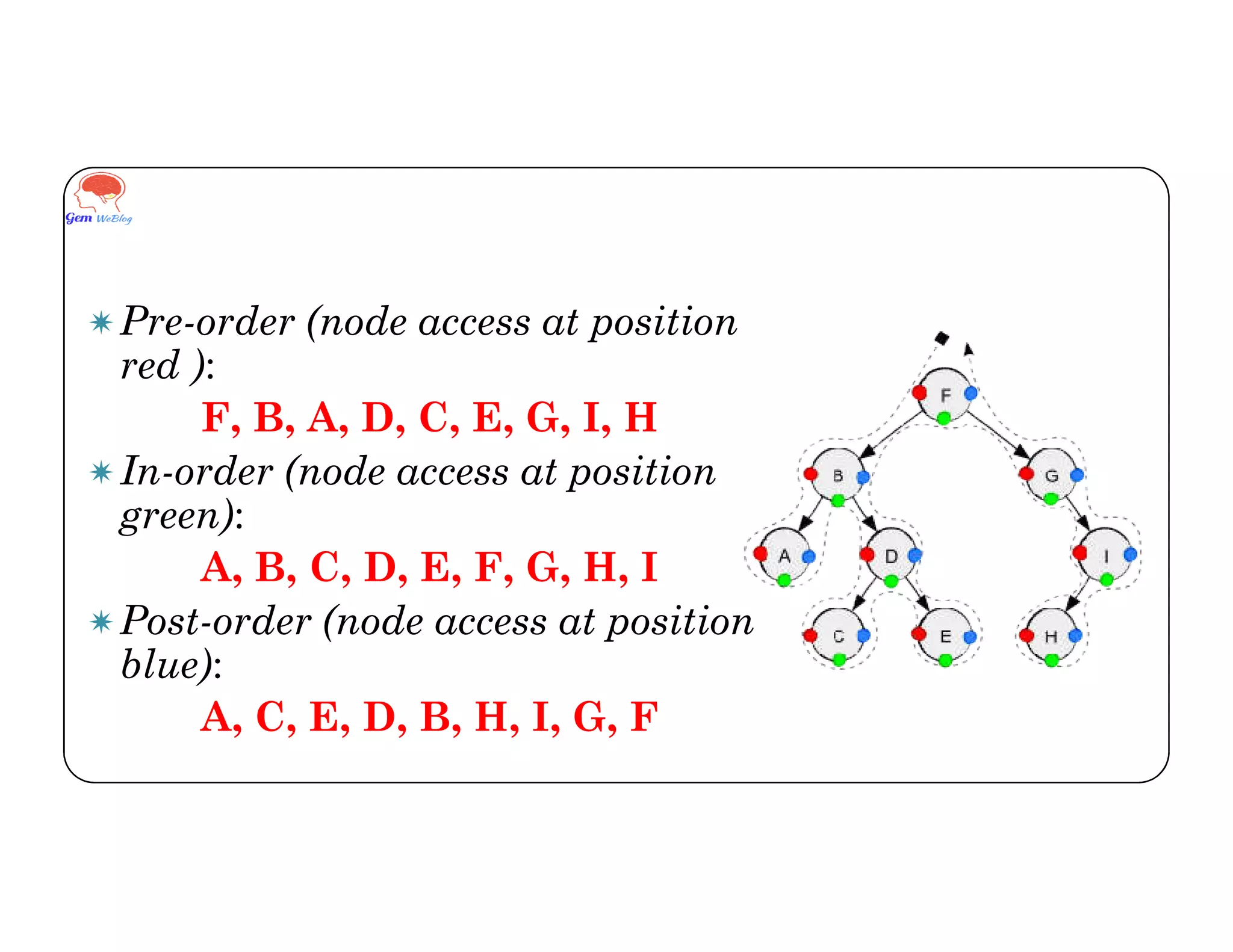
Binary tree traversals involve visiting each node exactly once in a defined order. There are three common traversal techniques: inorder, preorder, and postorder. Inorder traversal visits the left subtree, then the root, then the right subtree. Preorder visits the root, left subtree, then right subtree. Postorder visits the left subtree, right subtree, then the root. The order nodes are accessed depends on the traversal method used.

1. Binary Tree Traversals
Divide-and-Conquer Technique

2. Tree Traversal
 Also known as tree search and walking the tree
 Refers to the process of visiting each node in a tree data
structure exactly once
structure exactly once

3. Tree Traversal Technique
 Based on the order in which the nodes are visited,
 Inorder traversal L-Ro-R
 Preorder traversal Ro-L-R
 Postorder traversal L-R-Ro

4. Inorder traversal
Inorder(root)
 Traverse the left sub-tree,
(recursively call inorder(root -> left)
(recursively call inorder(root -> left)
 Visit and print the root node.
 Traverse the right sub-tree,
(recursively call inorder(root -> right)
Inorder: d, g, b, e, a, f, c

5. Preorder traversal
Preorder(root)
 Visit and print the root node.
 Traverse the left sub-tree,
(recursively call inorder(root -> left)
 Traverse the right sub-tree,
(recursively call inorder(root -> right)
Preorder: a, b, d, g, e, c, f

6. Postorder traversal
Preorder(root)
 Traverse the left sub-tree,
(recursively call inorder(root -> left)
(recursively call inorder(root -> left)
 Traverse the right sub-tree,
(recursively call inorder(root -> right)
 Visit and print the root node.
Postorder: g, d, e, b, f, c, a

8. Pre-order (node access at position
red ):
F, B, A, D, C, E, G, I, H
In-order (node access at position
In-order (node access at position
green):
A, B, C, D, E, F, G, H, I
Post-order (node access at position
blue):
A, C, E, D, B, H, I, G, F

9. External and Internal Node
 Number of external
nodes x is
always 1 more than
the number of
the number of
internal nodes n:
x = n + 1