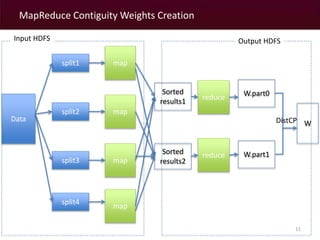
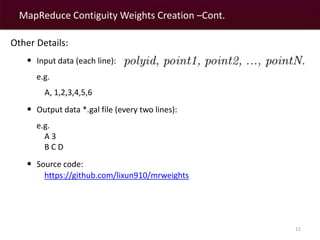
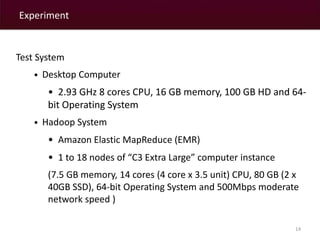
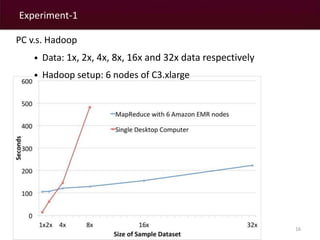
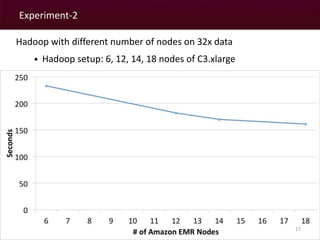
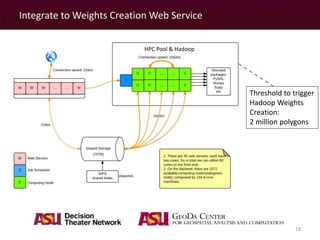
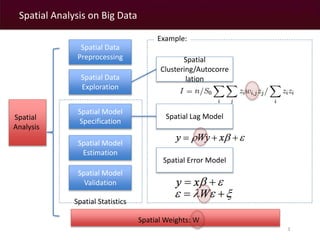
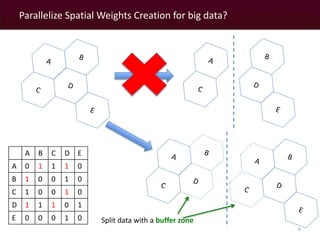
The document discusses a MapReduce algorithm developed to create contiguity weights for spatial analysis of large datasets. It outlines various methods for generating spatial weights, including counting algorithms for both rook and queen contiguity, and compares performances on different computing systems. The findings highlight potential issues of the algorithm, particularly concerning spatial neighbors without shared points or edges, and propose ongoing work to incorporate an r-tree structure to address these challenges.

1. The Problem
A MapReduce Algorithm to Create Contiguity
Weights for Spatial Analysis of Big Data
Xun Li, Wenwen Li, Luc Anselin, Sergio Rey, Julia
Nov 4, 2014
BIGSPATIAL 2014
Koschinsky
1

2. Big Spatial Data Challenge
Cyber-Framework: CyberGIS, Spatial Hadoop
2
Big Spatial Data Domain
Spatial
Data
Management
Computing
Grids
Super
Computers
HPC
Spatial
Analysis
Cloud Computing
Platform
Visualization
Spatial
Process
Modeling
Spatial
Pattern
Detection

3. Spatial Analysis on Big Data
3
Spatial
Analysis
Spatial Data
Preprocessing
Spatial Data
Exploration
Spatial Model
Specification
Spatial Model
Estimation
Spatial Model
Validation
Spatial
Clustering/Autocorre
lation
Spatial Lag Model
Spatial Error Model
Spatial Weights: W
Spatial Statistics
Example:

4. Spatial Weights
Spatial Weights
• Spatial weights is an essential component in spatial analysis where a
representation of spatial structure is needed.
• Tobler: “Everything is related to everything else, but near things are
more related to each other”.
Create Spatial Weights (W)
• Extract spatial structure:
• Spatial neighboring information (contiguity based weights)
• Spatial distance information (distance based weights)
4
A B C D E
A 0 1 0 0 0
B 1 0 1 1 0
C 0 1 0 1 1
D 0 1 1 0 0
E 0 0 1 0 0
A B C D E
2.5
2.5
3.5
A 0
1.2
B 1.2 0
2.3
0.7
C 2.3
0
1.1
D 0.7 1.1
0
E 0.3
0
4.5
0.3
2.5
2.5
3.5
4.5
0.1
0.1
Contiguity based Weights Distance based Weights

5. Contiguity Spatial Weights: how to find neighbors
5
Classic Algorithms:
• Brutal force search :
• Test A against B,C,D,E | B against C,D,E | C against D,E | D against E
• O(n2)
• Spatial Index :
• Binning algorithm
• r-tree index
O(n logn)
• Rook Contiguity:
neighbors share borders
• Queen Contiguity:
neighbors share borders or vertices

6. Parallelize Spatial Weights Creation for big data?
6
Split data with a buffer zone
A B C D E
A 0 1 1 1 0
B 1 0 0 1 0
C 1 0 0 1 0
D 1 1 1 0 1
E 0 0 0 1 0

7. Counting Algorithm for Contiguity Weights Creation
7
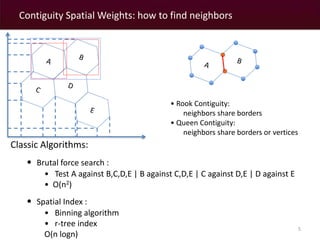
Counting Algorithms:
• Inspired by TopoJson:
• Same vertices only stored once.
• Counting how many polygons share a point (Queen Weights): O(n)
1
2
3 4
6
5
7
8
9
10
11
12
13
14
16
15
17
18
20
19
Count A:
{1:[A],
2:[A],
3:[A],
4:[A],
5:[A],
6:[A]}
Count B:
{1:[A]
,2:[A]
,3:[A]
,4:[A]
,5:[A,B]
,6:[A,B]
,7:[B]
,8:[B]
,9:[B]
,10:[B]}
Count C:
{1:[A]
,2:[A],
,3:[A,C]
,4:[A,C]
,5:[A,B]
,6:[A,B]
,7:[B]
,8:[B]
,9:[B]
,10:[B]
,13:[C]
,14:[C]
,15:[C]
,16:[C]}
Neighbors:
[A,C]
[A,B]

8. Counting Algorithm for Contiguity Weights Creation
8
Counting Algorithms:
• Counting how many polygons share an edge (Rook Weights): O(n)
1
2
3 4
6
5
7
8
9
10
11
12
13
14
16
15
17
18
20
19
Count A:
{(1,2):[A]
,(2,3):[A]
,(3,4):[A]
,(4,5):[A]
,(5,6):[A]
,(6,1):[A]}
Count B:
{(1,2):[A]
,(2,3):[A]
,(3,4):[A]
,(4,5):[A]
,(5,6):[A,B]
,(6,1):[A]
,(6,7):[B]
,(7,8):[B]
,(8,9):[B]
,(9,10):[B]}
Neighbors:
[A,B]

9. Parallel Counting Algorithm?
9
1
2
3 4
6
5
7
8
9
10
11
12
13
14
16
15
17
18
20
19
7
Count Results:
{1:[A]
,2:[A]
,3:[A,C]
,4:[A,C]
,5:[A]
,6:[A]
,13:[C]
,14:[C]
…}
Count Results:
{5:[B,D]
,6:[B]
…,9:[B]
,10:[B,D]
,11:[D,E]
,12:[D,E]
,13:[D]
…}
1
2
3 4
6
5
13
14
16
15
4
6
5
7
8
9
10
11
12
13
17
20
19
7

10. Parallel Counting Algorithm? –Conti.
10
Print line by line
1:[A]
2:[A]
3:[A,C]
4:[A,C]
5:[A]
6:[A]
13:[C]
14:[C]
…
Print line by line
5:[B,D]
6:[B]
…
9:[B]
10:[B,D]
11:[D,E]
12:[D,E]
13:[D]
…
1
2
3 4
6
5
13
14
16
15
4
6
5
7
8
9
10
11
12
13
17
20
19
7
Merge & Sort
Two Results:
1:[A]
2:[A]
3:[A,C]
4:[A,C]
4:[A]
4:[D]
5:[A]
5:[B,D]
6:[A]
6:[B]
7:[B]
11:[D,E]
12:[D,E]
13:[C]
13:[D]
14:[C]
…
{3:[A,C]}
{4:[A,C,D]}
{5:[A,B,D]}
{6:[A,B]}
{11:[D,E]}
{12:[D,E]}
{13:[C,D]}
A B C D E
A 0 1 1 1 0
B 1 0 0 1 0
C 1 0 0 1 0
D 1 1 1 0 1
E 0 0 0 1 0

11. MapReduce Contiguity Weights Creation
11
Input HDFS Output HDFS
Data
split1
split2
split3
split4
map
map
map
map
Sorted
results1
Sorted
results2
reduce
reduce
W.part0
W.part1
DistCP W

12. MapReduce Contiguity Weights Creation –Cont.
12
Other Details:
• Input data (each line):
e.g.
A, 1,2,3,4,5,6
• Output data *.gal file (every two lines):
e.g.
A 3
B C D
• Source code:
https://github.com/lixun910/mrweights

13. Experiments
13
Original Data:
• parcel data of Chicago city in the United States
• 592,521 polygons
Artificial Big Data:
• Duplicate original data several times side by side
• For example: a 4x original data with 2,370,084 polygons
• The largest test data is a 32x original data

14. Experiment
14
Test System
• Desktop Computer
• 2.93 GHz 8 cores CPU, 16 GB memory, 100 GB HD and 64-
bit Operating System
• Hadoop System
• Amazon Elastic MapReduce (EMR)
• 1 to 18 nodes of “C3 Extra Large” computer instance
(7.5 GB memory, 14 cores (4 core x 3.5 unit) CPU, 80 GB (2 x
40GB SSD), 64-bit Operating System and 500Mbps moderate
network speed )

15. Experiment
15
Code/Application
• Desktop version (Python)
• No parallel
• Hadoop version (Python)
• Executed via Hadoop streaming pipeline

16. Experiment-1
16
PC v.s. Hadoop
• Data: 1x, 2x, 4x, 8x, 16x and 32x data respectively
• Hadoop setup: 6 nodes of C3.xlarge

17. Experiment-2
17
Hadoop with different number of nodes on 32x data
• Hadoop setup: 6, 12, 14, 18 nodes of C3.xlarge

18. Integrate to Weights Creation Web Service
18
HPC Pool & Hadoop
Threshold to trigger
Hadoop Weights
Creation:
2 million polygons

19. Issues
19
• This algorithm won’t work when spatial neighbors do not share
points or edges (it requires the shared points are exactly same)
• This algorithm can’t generate distance based weights
• Potential solution
• Use MapReduce r-tree (SpatialHadoop)

20. Conclusion
• Contribution: a MapReduce algorithm to create
contiguity weights matrix for big spatial data
• Ongoing work: use existing MapReduce r-tree to solve
the potential issues of this algorithm
20

21. Thanks!
The Problem
Nov 4, 2014
BIGSPATIAL 2014
21