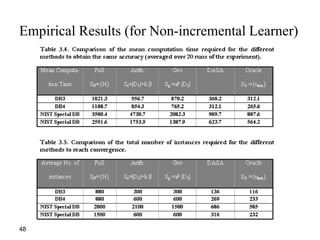
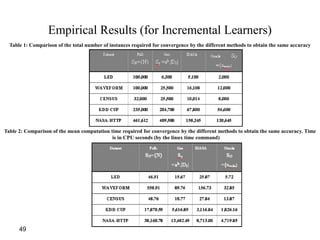
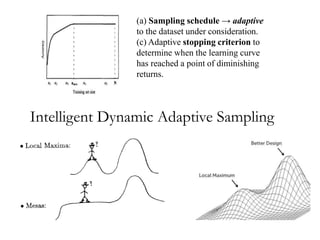
The document discusses big data challenges and potential solutions. It begins by outlining how big data is generated from various sources and used in applications like search engines. The main challenges are determining which subset of big data to analyze and how to clean noisy data. Two potential solutions discussed are: 1) Intelligent sampling to determine a representative subset of data to analyze instead of the entire dataset, in order to improve running time. Adaptive sampling techniques like IDASA are proposed. 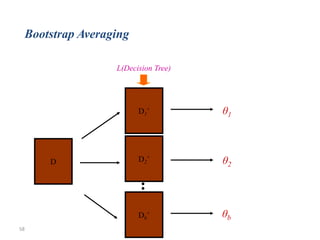2) Filtering techniques like ensemble filtering use multiple models to identify and remove mislabeled instances from training data, in order to improve predictive accuracy by cleaning the data. Bayesian analysis can interpret filtering as a form of model averaging.

1. Big Data : Challenges & Potential
Solutions
Ashwin Satyanarayana
CST Colloquium
April 16th, 2015

2. Outline
• Big Data Everywhere
• Motivation (How Big Data solves Speller Issue)
• The New Bottleneck in Big Data
• Search Engine (Big Data)
– Query Document Mismatch
– Query Reformulation
• Potential Solutions
– How much of the data?
• Intelligent Sampling of Big Data
– How to clean up the data?
• Filtering
• Conclusions

3. Big Data EveryWhere!
• Umbrella term – digital data to health data
• Big data gets its name from the massive amounts of
zeros and ones collected in a single year, month, day
— even an hour.
• Lots of data is being collected
and warehoused
– Web data, e-commerce
– purchases at department/
grocery stores
– Bank/Credit Card
transactions
– Social Network

4. How much data?
640K ought to be
enough for anybody.

5. Opportunities?

7. Big Data and the U.S. Gov't
• "It's about discovering meaning
and information from millions
and billions of data points… We
therefore can't overstate the
need for software engineers …
working together to find new
and faster ways to identify and
separate relevant data from non-
relevant data"
– Janet Napolitano, March 2011

9. Where are we headed?
• Smart Data
– employees can promote content targeting potential customers.
• Identity Data
– your identity data tells the story of who you are in the digital age, including
what you like, what you buy, your lifestyle choices and at what time or
intervals all of this occurs.
• People Data
– who your audience likes and follows on social media, what links they click,
how long they stay on the site that they clicked over to and how many
converted versus bounced.
– based on people data combined with on-site analytics, a site can customize
experiences for users based how those customers want to use a site.

10. Big Data – How does it solve
problems?
Motivating Example: Speller Problem Solved!

11. Speller
Google Speller
Microsoft Word Speller

12. More Data beats Better Algorithms
• Before (Big Data)
• Now (Big Data)
Algorithms
Data
Data
Algorithms

13. User Click Data is the key!
• User types a query A, no click
• User alters the query to B, and click on a result
• Google/Bing captures that information: A -> B
• If many users use the same alteration from A to B, then
google knows that B is the better alteration for A.
• “Farenheight” -> “Fahrenheit” -> Click
– Farenheight -> Fahrenheit -> 1045 times
– Farenheight -> Fare height -> 3 times
• Thus, Google/Bing uses the most often made transition
that results in a click to offer spell suggestions.

14. Other Search Engine Problems
Solved using Big Data

32. New Bottleneck
• Hardware was the primary bottleneck with thin
network pipes, small hard disks and slow processors.
– As hardware improved,
– Software that distributed storage and processing across
large numbers of independent servers.
• Hadoop is the software platform - “collect everything.”
• Instead of spending vast amounts of time sifting
through an avalanche of data, data scientists need
tools to determine what subset of data to analyze and
how to clean and make sense of it.

33. 33
Motivation: Training a Neural Network
for Face Recognition
Neural Net MaleFemale
Training
M M M M M M M M M M
M M M M M M M M M M
M M M M M M M M M M
M M M M M M M M M M
F F F F F F F F F F
M M M M M M M M M M

34. 34
Motivation: Face Recognition
• Challenge 1: How many faces from a
large database are needed to train a
system so that it would distinguish
between a male and a female?
Is this enough?

35. 35
Motivation: Face Recognition
• Challenge 2: Predictive accuracy
depends on the quality of data in the
training set. Hence improving the quality
of training data (i.e. handling noise)
improves the accuracy over unseen
instances.
Female
Female
Training Instance Class Label
Male
NonoiseFeaturenoiseClassnoise
Noise

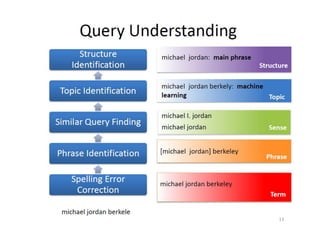
36. 36
The Curse of Large Datasets
There are two main challenges of dealing with large datasets.
• Running Time: Reducing the amount of time it takes for the mining
algorithm to train.
• Predictive Accuracy: Poor quality of instances in training data lead
to lower predictive accuracies. Large datasets are usually
heterogeneous, and subjected to more noisy instances [Liu, Motoda
DMKD 2002].
The goal of our work is to address these questions and provide some
solutions.

37. 37
Two Potential Solutions
• There are two potential solutions to the problems
• Running time:
– Scale up existing data mining algorithms (for e.g.
parallelize them)
– Scale down the data
• Predictive accuracy:
– Better mining algorithms
– Improve the quality of the training data
Intelligent Sampling
Bootstrapping
 We shall focus on first scaling down the data, while improving the quality

38. 38
Learning Curve Phenomenon
• Is it necessary to apply learner
to all of the available data?
• A learning curve depicts the
relationship between sample
size and accuracy [Provost,
Jensen & Oates 99].
• Problem: Determining nmin efficiently
Given a data mining algorithm M, a dataset D of N instances, we would like the
smallest sample Di of size nmin such that:
Pr(acc(D) – acc(Di) > ε) ≤ δ
ε is the maximum acceptable decrease in accuracy (approximation) and
δ is the probability of failure

39. 39
Prior Work: Static Sampling
• Arithmetic Sampling [John & Langley
KDD 1996] uses a schedule
Sa = <n0, n0 + nδ, n0 + 2nδ,..n0+k.nδ>
Example: An example arithmetic
schedule is <100 , 200, 300, . . . .>
Drawback: If nmin is a large multiple of
nδ, then the approach will require many
runs of the underlying algorithm.
The total number of instances used may
be greater than N.

40. 40
Prior Work in Progressive Sampling
• Geometric Sampling [Provost, Jenson &
Oates KDD 1999] uses a schedule
Sg= <n0, a.n0,a2.n0, ………,ak.n0>
An example geometric schedule is:
<100,200,400,800, . . .>
Drawbacks:
(a) In practice, Geometric Sampling
suffers from overshooting nmin.
(b) Not dependent on the dataset at
hand. A good sampling algorithm
is expected to have low bias and
low sampling variance
For example in the KDD CUP dataset,
when nmin=56,600,
the geometric schedule is as follows:
{100, 200, 400, 800, 1600, 3200, 6400,
12800, 25600, 51200, 102400}.
Notice here that the last sample has
overshot nmin by 45,800 instances

41. Intelligent Dynamic Adaptive Sampling
(a) Sampling schedule → adaptive
to the dataset under consideration.
(c) Adaptive stopping criterion to
determine when the learning curve
has reached a point of diminishing
returns.

42. 42
Definition: Chebyshev Inequality
• Definition 1: Chebyshev Inequality [Bertrand and Chebyshev-1845]: In any
probability distribution, the probability of the estimated quantity p’ being more than
epsilon far away from the true value p after m independently drawn points is
bounded by:
m
1
p'
]|p'-p|Pr[ 22
2










 


 







m
1
p'
]|p'-p|Pr[ 22
2
What are we trying to solve?
Pr(acc(D) – acc(Dnmin) > ε) ≤ δ
Challenge: how do we compute the accuracy of the entire dataset acc(D)?

43. Myopic Strategy: One Step at a time
43
û(Di)
û(Di+1)


||
1
)(
||
1
)
i
û(D
iD
i
i
i
xf
D
[Average over the sample Di]
The instance function f(xi) used here is a
Bernoulli trial, 0-1 classification accuracy

44. 44



 







m
1
p'
]|p'-p|Pr[ 22
2
True value
u(Da)-u(Db);
where |Da|>|Db|>nmin
Estimated value
u(Da)-u(Db);
where |Da|>|Db|≥1
Plateau Region:
p=0
Myopic Strategy:
u(Di) - u(Di-1)
   


 







m
BOOT 1
))u(D-)u(D(
)u(D-)u(D-0Pr 2
1-ii
2
2
1-ii

 1
))u(D-)u(D( 2
1-ii
2
2







 BOOT
m 








 m
BOOT 1
))u(D-)u(D( 2
1-ii
2
2
Approximation parameter
Confidence parameter
Bootstrapped Variance p’
(to improve the quality of the training data)

45. 45
Four Possible cases for Convergence
NegativeFalse
1
p'
and|p'-p|(d)
PositiveFalse
1
p'
and|p'-p|(c)
instancesmoreAdd
1
p'
and|p'-p|(b)
Converged
1
p'
and|p'-p|(a)
22
2
22
2
22
2
22
2
















































m
m
m
m

46. 46

47. 47
Empirical Results
• (Full): SN = <N>, a single sample with all the instances. This is the most commonly
used method. This method suffers from both speed and memory drawbacks.
• (Geo): Geometric Sampling, in which the training set size is increased
geometrically, Sg = <|D1|,a.|D1|,a2.|D1|,a3.|D1|….ak.|D1|> until convergence is
reached. In our experiments, we use |D1|=100, and a=2 as per the Provost et’ al
study.
• (IDASA): Our adaptive sampling approach using Chebyshev Bounds. We use ε =
0.001 and δ = 0.05 (95% probability) in all our experiments.
• (Oracle): So = <nmin>, the optimal schedule determined by an omniscient oracle; we
determined nmin empirically by analyzing the full learning curve beforehand. We use
these results to empirically compare the optimum performance with other methods.
• We compare these methods using the following two performance criteria:
• (a) The mean computation time: Averaged over 20 runs for each dataset.
• (b) The total number of instances needed to converge: If the sampling schedule, is
as follows: S={|D1|,|D2|,|D3|….|Dk|}, then the total number of instances would be
|D1|+|D2|+|D3|….+|Dk|.

48. 48
Empirical Results (for Non-incremental Learner)

49. 49
Empirical Results (for Incremental Learners)
Table 2: Comparison of the mean computation time required for convergence by the different methods to obtain the same accuracy. Time
is in CPU seconds (by the linux time command)
Table 1: Comparison of the total number of instances required for convergence by the different methods to obtain the same accuracy

50. 50
Conclusions
1) Big data is evolving and Smart data, Identity data and People data are here to stay.
Think of them as the human discovery of fire, the wheel and wheat.
2) Search Engines use Big Data for their relevance and ranking problems
3) Main Bottleneck: data scientists need tools to determine what subset of data to
analyze and how to clean and make sense of it
4) Intelligent Sampling addresses what subset to use.
5) Bootstrap filtering helps clean up the data.
6) In conclusion, Big data is big and it is here to stay. And it’s only getting bigger!!

51. 51
Questions & Suggestions

52. Filtering

53. 53
Bayesian Analysis of Ensemble Filtering
L1(k-NN Classifier)
Training Data
D
L3(Linear Machine)L2(Decision Tree)
θ1
θ3
θ2
θ1 δ(yj , θ1(xj))
θ2
δ(yj , θ2(xj))
θ3
δ(yj , θ3(xj))
=1 if θ
.(xj) is the same as
the true label yj else 0
( xj , yj )

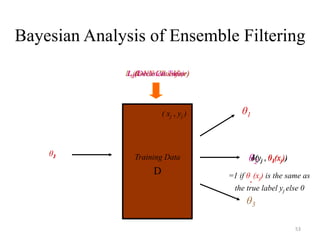
54. 54
Bayesian Analysis of Filtering
Techniques
• Bayesian Analysis of Ensemble Filtering:
– Ensemble Filtering [Brodley & Friedl 1999- JAIR]: An ensemble classifier detects
mislabeled instances by constructing a set of classifiers (m base level detectors).
– A majority vote filter tags an instance as mislabeled if more than half of the m
classifiers classify it incorrectly
– If < ½ then the instance is noisy and is removed
– Example: Say δ(yj ,θ1(xj)) =1 (non-noisy)
δ(yj ,θ2(xj)) =0 (noisy)
δ(yj ,θ3(xj)) =0 (noisy)
Pr(y|x,Θ*) = 1/3 =0.33 < ½ , The instance xj is treated as noisy and is removed.
  


*
,
||
1
),|Pr( *
*

 xtxty
),|Pr( *
 xty

55. 55
What Computation is Being Performed?
   


*
)(|
1
,|Pr *
i
xty
k
xty i


),|Pr(
1
*
ixty
k i





The computation can be interpreted as a crude form of model averaging which
ignores predictive uncertainty and model uncertainty
)|Pr(),|Pr(
*
Dxty ii
i


 

Assigns equal weight to all the models “Probability” that the model
predicts the correct output

56. 56
Bootstrapped Model Averaging
– Now that we know what computation is occurring in
the filtering techniques, we now propose using a better
approximation to model averaging.
– There are lots of model averaging approaches, we
choose this because it is efficient for large datasets.
– This particular case uses Efron’s non-parametric
bootstrapping approach which is as shown below:
where the datasets D’ are the different bootstrap
samples generated from the original dataset D.
     DDxyxy
DLD
i
i
|'Pr,|Pr,|Pr
)'(,'
 



57. 57
Introduction to Bootstrapping
• Basic idea:
– Draw datasets by sampling with replacement from the original dataset
– Each perturbed dataset has the same size as the original training set
D
Db’
D2’
D1’

58. 58
Bootstrap Averaging
D
Db’
D2’
D1’
L(Decision Tree)
θ1
θ2
θb

59. 59
Bootstrapped Model Averaging (BMA) vs Filtering
• We now try using bootstrapped model averaging and compare it with partition filtering
(10 folds). We used 80% training set and a fixed 20% for testing. We eliminate noisy
instances as in partition filtering, and obtained the following results:
• Thus we see can conclude that bootstrap averaged model produces a better
approximation to model averaging when compared to the model averaging performed by
filtering.
2500 instances -> 10% noise – 250 noisy instances
Partition filtering removed – 194 instances (162 instances were actually noisy, 32 instances were good ones)
BMA filtering removed – 189 instances (178 instances were noisy, 11 instances were non-noisy)
Overlap of noisy instances between the two techniques = 151 instances
LED24 Dataset

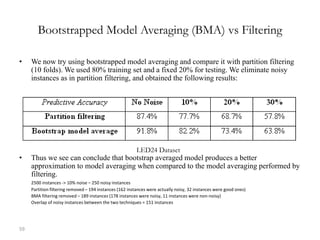
60. 60
Why remove noise?
• 1) Removing noisy instances increases
the predictive accuracy. This has been
shown by Quinlan [Qui86] and Brodley
and Friedl ([BF96][BF99])
• 2) Removing noisy instances creates a
simpler model. We show this empirically
in the Table.
• 3) Removing noisy instances reduces the
variance of the predictive accuracy: This
makes a more stable learner whose
accuracy estimate is more likely to be the
true value.

61. 61
Motivation for Correction: Spell
Checker
Filter
Correct

62. 62
Empirical Comparison of Noise Handling Techniques
• We compare the following approaches for noise
handling:
– Robust Algorithms: To avoid overfitting, post pruning
and stop conditions are used that prevent further
splitting of a leaf node.
– Partition Filtering: Discards instances that the C4.5
decision tree misclassifies, and builds a new tree using
the remaining data
– LC Approach: Corrects instances that the C4.5 decision
tree misclassified and built a new tree using the
corrected data.

63. 63
Empirical Results

64. 64
Empirical Results

65. Conclusion
65
Our research yielded the following results:
• (What size?) Sampling:
– Dynamic Adaptive Sampling using Chernoff
Inequality
– General purpose Adaptive Sampling using Chebyshev
Inequality
• (Cleaning) Filtering:
– Bayesian Analysis of other filtering techniques
– Bootstrap Model Averaging for Noise Removal
– LC Approach

66. 66
Questions & Suggestions