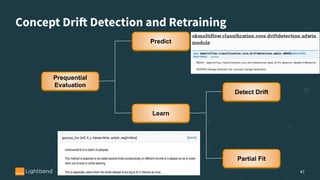
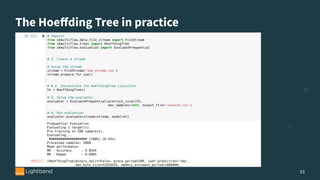
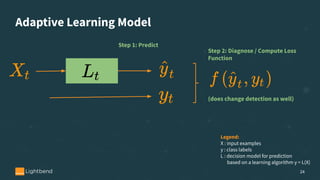
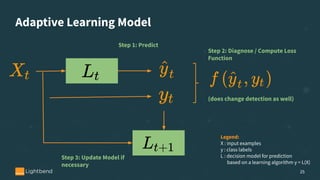
The document discusses online machine learning in streaming applications, emphasizing the differences between data streams and static datasets, as well as the challenges of stream-based learning, such as concept drift and evolving feature spaces. It covers learning systems' desirable properties, evaluation metrics, and specific algorithms like the Adwin algorithm and Hoeffding tree classifiers for handling real-time data. The presentation highlights the adaptive learning model necessary for processing continuous data while managing memory constraints and adapting to changes in data distribution.

1. Online Machine Learning in
Streaming Applications
Stavros Kontopoulos (Principal Engineer, Lightbend)
@s_kontopoulos
&
Debasish Ghosh (Principal Engineer, Lightbend)
@debasishg
{stavros.kontopoulos, debasish.ghosh}@lightbend.com

2. Agenda
• Data Streams meet Machine Learning. How they differ from
static data sets.
• Learning systems for data streams
• Adaptive learning model
• Evaluation metrics
• The ADWIN algorithm and the complete cycle of training
streaming systems
• The Hoeffding Tree based classifiers
2

3. Formalizing Data Streams
● Difference with batch learning using
static data sets
● The data stream model
● Challenges of stream based learning

4. Batch Learning
• Static data set to generate an output
hypothesis
• One shot data analysis - fixed stable
feature space
• Assume stationarity of data
4

5. Batch and Online Learning
• Static data set to generate an output
hypothesis
• One shot data analysis - fixed stable
feature space
• Assume stationarity of data
5
• Learner operates on a (potentially
infinite) sequence of data streams
• Evolving feature space - new learning
paradigm Feature Evolvable
Streaming Learning
• Non stationary data set - leading to
concept drift

6. Formalizing Data Streams
• Data streams are ordered sequences of data
elements: S = (s1
, s2
, …, sn
) where n can
potentially be infinite
• data arrives continuously
• in a potentially infinite stream
• that has to be processed by a resource constrained
system
6

7. Challenges of Stream-based Learning
● Very large (potentially infinite) number of data elements - think
sublinear space
● High rate of data arrival at the system - may need to think of
sampling
● Changes in data distribution during stream processing, which
can affect prediction - concept drift
7

8. Learning Systems for Data Streams
● Dimensions of learning
● Classification problems
● Concept drift

9. Learning Systems for Data Streams
Desirable properties of learning systems for efficiently mining continuous,
high-volume, open ended data streams (Hulten and Domingoes, 20011
):
● Require small constant time per data example
● Use fixed amount of main memory, irrespective of the number of
examples
● Build a decision model using a single scan over the training data
● Generate an anytime model independent of the order of the examples
● Ability to deal with concept drift
1
Hulten, G., & Domingos, P. (2001). Catching up with the data: research issues in mining data streams. In Proc. of workshop on research
issues in data mining and knowledge discovery, Santa Barbara, USA.
9

10. Dimensions of Learning
● Space - the available memory is fixed
● Learning Time - process incoming examples at the rate
they arrive
● Generalization Power - how effective the model is at
capturing the true underlying concept
10

11. Classification Problems
• Learn concepts from a static dataset, instances of
which belong to an underlying distribution
defined by a generating function
• This dataset is assumed to contain all
information necessary to learn all the concepts
pertaining to the underlying generating function
11

12. Classification Problems
12
Legend:
X : input examples
y : class labels
Prior probabilities of
the class labels
Class conditional probability
density functions
Prior probabilities of
the class labels
Beliefs before the start
of the experiment
Probability function of X
given the class label y

13. Classification Problems
13
Legend:
X : input examples
y : class labels
Prior probabilities of
the class labels
Class conditional probability
density functions
Posterior - Probability that the sample to
be classified is a y, given the data set

14. Concept
14
(Prior)
(Class conditional)
The joint distribution gives us
the stochastic definition of a
Concept
For unsupervised learning where we
don't have the class labels, Concept is

15. Streaming Classification Assumptions
• Data are not necessarily iid
• Solutions are approximate based on one pass of the data
• Error Estimation requires special estimators for non-stationary
distributions: Prequential Accuracy
• if example per class distribution is imbalanced use the Cohen statistic
(Kappa statistic)
• McNemar's test or Q testing with fading factors for statistical
significance when comparing two classifiers
• If distribution is stationary a holdout approach can be used.
15

16. Concept Drift
Because data is expected to evolve over time, especially in
dynamically changing environments, where non stationarity is
typical, the underlying distribution can change dynamically over
time.
Concept drift between time point t0
and time point t1
can be
defined as:
16

17. How does Concept Drift Affect Classification
Problems
17
• Classification decision is made based on the
posterior probabilities of the classes
may changemay change
may change

18. How does Concept Drift Affect Classification
Problems
18
affects predictive decision
changes in data
distribution without
knowing the class labels
Real Concept Drift
Virtual Concept Drift
does not affect the target concept, but
can lead to changes in the decision
boundary

19. Real and Virtual Concept Drifts
19
(Source) A Survey on Concept Drift Adaptation - Joao Gama et al. ACM Computing Surveys, 46, 4, March 2014
DOI: http://dx.doi.org/10.1145/2523813

20. Concept Drift in Classification Problems - ad Click
Prediction
20
Legend:
X : input examples
y : class labels
Some ads may suddenly grow
in high demand
User profile may change
User preferences may change affecting
classification

21. Adaptive Learning Model
● how to adapt to evolving data over time
● detecting concept drift and adapting to it

22. Adaptive Learning Model
● Detect and adapt to evolving data over time
● Adapt decision model to take care of concept drift
○ Detect drift
○ Adapt
○ Operate in less than example arrival time and
○ Use not more than a fixed amount of memory for any
storage.
22

23. Adaptive Learning Model
23
Legend:
X : input examples
y : class labels
L : decision model for prediction
based on a learning algorithm y = L(X)
Step 1: Predict

24. Adaptive Learning Model
24
Legend:
X : input examples
y : class labels
L : decision model for prediction
based on a learning algorithm y = L(X)
Step 1: Predict
Step 2: Diagnose / Compute Loss
Function
(does change detection as well)

25. Adaptive Learning Model
25
Legend:
X : input examples
y : class labels
L : decision model for prediction
based on a learning algorithm y = L(X)
Step 1: Predict
Step 2: Diagnose / Compute Loss
Function
Step 3: Update Model if
necessary
(does change detection as well)

26. 26
João Gama, Indrė Žliobaitė, Albert Bifet, Mykola Pechenizkiy, and Abdelhamid Bouchachia. 2014. A survey
on concept drift adaptation. ACM Comput. Surv. 46, 4, Article 44 (March 2014), 37 pages. DOI:
https://doi.org/10.1145/2523813

27. Evaluation Metrics
● Difference from batch mode
● Prequential evaluation model (test-then-train)

28. Evaluation Metrics - Batch
Examples of the form of pairs Decision Model output
Error!
Error rate is the probability of observing
Learning Model
(Train)

29. Evaluation Metrics - Streaming
• Incorporate new information at the speed data arrives
• Detect changes and adapt the model to the most recent
information
• Forget outdated information

30. Evaluation Metrics - Streaming
30
• The Predictive Sequential approach
• for each example
• First: Predict
• Second: Compute loss whenever target is available
• Now we can define the Prequential Error, computed at time t, based on a
accumulated sum of a loss function between prediction and observed
values

31. Prequential Evaluation
• Evolution of learning as a process
• The model becomes better and better as we see more and
more examples
• Recency is important - compute the prequential error using a
forgetting mechanism
31

32. Forgetting mechanism for error estimation
● Prequential accuracy over a sliding window of a specific size
with the most recent observations
● Fading factors that weigh observations using a decay factor
𝛂
32

33. Techniques to overcome Concept Drift
● The ADWIN Algorithm - based on sliding windows of dynamic size, where
the algorithm ensures that the window of data closely approximates the current
concept distribution
● Hoeffding Adaptive Trees - a data structure where the base learner is able
to adapt to new training data in case of concept drift

34. An Adaptive Windowing Algorithm with
forgetfulness
34

35. The ADWIN Algorithm
● Windows of varying size (recomputed online)
● Automatically grows the window when no change occurs and shrinks it
when data changes
● Whenever two “large enough” sub-windows exhibit “distinct enough”
averages
○ We can conclude that the corresponding “expected values” are
different
○ The older portion of the window is dropped
35

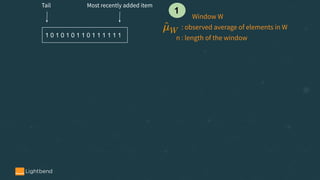
36. The ADWIN Algorithm - Notations and Settings
• a (possibly infinite) sequence of real values x1
, x2
, .. , xt
, ..
• a confidence value 𝛿 ∈ (0, 1)
• the value of xt
is available only at time t
• each xt
is generated according to some distribution Dt
independent of every t
• 𝜇t
and 𝜎t
2
denote the expected value and variance of xt
when it is drawn according to Dt
• xt
is always in [0, 1]
36

37. 1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
Window W
: observed average of elements in W
Tail Most recently added item
n : length of the window
1

38. 1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
Window W
: observed average of elements in W
Tail Most recently added item
n : length of the window
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
W0
W1
W0
W1
W0
W1
Split into subwindows of lengths n0
and n1
such that n0
+ n1
= n
1
2

39. 39
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
Window W
: observed average of elements in W
Tail Most recently added item
n : length of the window
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
W0
W1
W0
W1
W0
W1
Split into subwindows of lengths n0
and n1
such that n0
+ n1
= n For each of the subwindows check if
: average of elements in W0
: average of elements in W1
1
2 3
: threshold depending on n, n0
, n1
and the confidence level of the
algorithm

40. 40
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
Window W
: observed average of elements in W
Tail Most recently added item
n : length of the window
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
1 0 1 0 1 0 1 1 0 1 1 1 1 1 1
W0
W1
W0
W1
W0
W1
Split into subwindows of lengths n0
and n1
such that n0
+ n1
= n For each of the subwindows check if
: average of elements in W0
: average of elements in W1
1
2 3
: threshold depending on n, n0
, n1
and the confidence level of the
algorithm
Whenever this happens, drop W0
from W
and the window compresses
4

41. The ADWIN Algorithm
● By using an Exponential Histogram with b buckets to keep the
average of the window W in O(logW) space, ADWIN checks b-1
times the mean.
41

42. The ADWIN Algorithm
● When observed average in both subwindows differs by more
than the threshold, the old part is discarded
● The new part gives the new correct mean
● ADWIN is not just a heuristic algorithm (unlike many of its
predecessors), it comes with theoretical guarantees on the
rates of false positives and false negatives and the size
related to the rate of change
42

43. 43
Prequential
Evaluation
Concept Drift Detection and Retraining

44. 44
Prequential
Evaluation
Predict
Learn
Concept Drift Detection and Retraining

45. 45
Prequential
Evaluation
Predict
Learn
Detect Drift
Partial Fit
Concept Drift Detection and Retraining

46. 46
Prequential
Evaluation
Predict
Learn
Detect Drift
Partial Fit
Concept Drift Detection and Retraining

47. 47
Prequential
Evaluation
Predict
Learn
Detect Drift
Partial Fit
Concept Drift Detection and Retraining

48. 48

49. The Hoeffding Tree Classifier
• Incremental decision tree using constant space and constant time per
example
• Uses Hoeffding bounds to guarantee that its output is asymptotically
nearly identical to a conventional learner
• Designed for unbounded data sets
• Works very well in practice and has proven performance that is close to a
batch classifier performance with infinite training examples.
49

50. The Hoeffding Tree
Key Steps for each training instance (x,yk
) that belongs
to class k:
1. Calculate all G split values at root and the counters
nijk
. G can be based on InfoGain = Entropy(S) -
Entropy(S,A) etc.
2. Recursively decide to split based on the difference
of the G values of the two best attributes (say with
confidence that these two are different). Also check
with the baseline G value at the current tree node
(eg. using majority class or Naive Bayes etc).
50

51. The Hoeffding Tree - Splitting Bound
51

52. The Hoeffding Tree
Later improvements:
• VFDT, CVFDT (concept drift support and using a sliding
window), VFDTc & UFFT (numeric values and concept drift
support)
• Hoeffding Adaptive Tree (uses ADWIN for the concept drift)
Common G functions like Gini Index cannot be expressed as
independent random variables so formally the Hoeffding bound
is not appropriate but works in practice. McDiarmid inequality is
considered state of the art in this area.
52

53. The Hoeffding Tree in practice
53

54. The Hoeffding Adaptive Tree
Key idea: Whenever change
is detected as we traverse a
node, we start a new
sub-tree.
54

55. Demo
https://github.com/debasishg/strata-ny-2019/blob/master/conce
pt-drift/test-GaussianNB.ipynb
55

56. 56

57. Thank You Stavros Kontopoulos
stavros.kontopoulos@lightbend.com
@s_kontopoulos
Debasish Ghosh
debasish.ghosh@lightbend.com
@debasishg