안녕하세요 딥러닝 논문 읽기 모임입니다. 오늘 업로드된 논문 리뷰 영상은 NeurIPS 2020 에 발표된 'Big Bird - Transformers for Longer Sequences'라는 제목의 논문입니다.
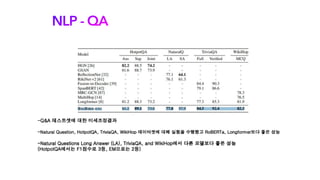
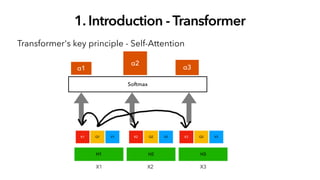
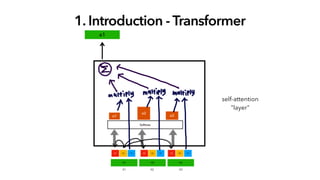
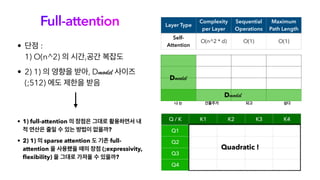
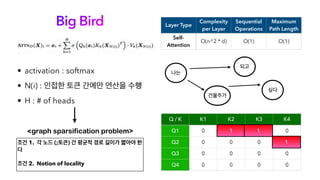
오늘 소개해 드릴 논문은 Big Bird로, Transformer 계열 논문들의 Full Attention 구조의 한계를 리캡하고, Long Sequence의 처리를 매우 효율적으로 처리하기 위함을 목표로 나온 논문입니다. 트랜스포머의 엄청난 성능은 이미 다들 잘 알고 계시지만, 시퀀스 길이가 길어질수록 연산의 한계에 부딪히게 되는데, 이에 많은 논문이 비효율적인 연산을 줄이고자 많은 시도가 있었고, Big Bird도 그중 하나의 논문이라고 생각해 주시면 됩니다. 오늘 논문 리뷰를 위해 자연어 처리팀 백지윤 님이 자세한 리뷰 도와주셨습니다.








![1. Universal Approximators
“ 어떠한 star graph 를 포함하는 sparse
attention mechanism 도 모두 universal
approximator 이 될 수 있다 ”
• Fcd : permutation equivariant 하고 범위가 무한대가 아닌 bounded 된 function space
f: [0,1]nxd -> ℝnxd (n : # of tokens, d : d-dimensional embeddings)
• TD : H ; # of heads, m ; head size, q ; hidden layer dim
• d (f,g) :
H,m,q
p
https://www.youtube.com/watch?v=sfy6qJIRyvg&t=1551s
<Are Transformers universal approximators of sequence-to-sequence functions?>](https://image.slidesharecdn.com/bigbird-211230090217/85/Big-Bird-Transformers-for-Longer-Sequences-16-320.jpg)
![1. Universal Approximators
“ 어떠한 star graph 를 포함하는 sparse
attention mechanism 도 모두 universal
approximator 이 될 수 있다 ”
Approximate Fcd by piece-wise constant functions using Feed Forward
https://www.youtube.com/watch?v=sfy6qJIRyvg&t=1551s
<Are Transformers universal approximators of sequence-to-sequence functions?>
STEP 1.
• Fcd : permutation equivariant 하고 범위가 무한대가 아닌 bounded 된 function space
[0,1]nxd -> G = {0,δ,2δ, …,1-δ}nxd
Delta cubes](https://image.slidesharecdn.com/bigbird-211230090217/85/Big-Bird-Transformers-for-Longer-Sequences-17-320.jpg)