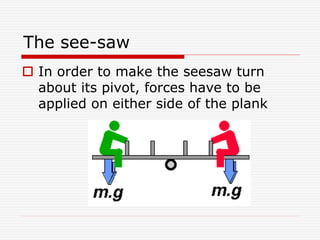
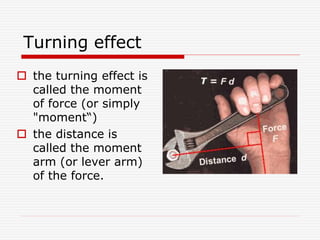
This document discusses moments and torque. It defines moment as the turning effect of a force, which is calculated as the product of the force and its perpendicular distance from the pivot. The seesaw is used as an example, where the person sitting closer to the fulcrum needs less force to balance someone further away. Center of gravity is also discussed, along with an example calculating an unknown balancing weight on a seesaw. Finally, the document defines a couple as two parallel opposing forces that create torque, calculated as the product of one force and the distance between them.

1. Moment of a Force

2. Name:Purva Avinash Adam
Roll no:01
Grade:X
Subject : Physics
Guide Teacher:Miss Suchita Dambre
Academic year :2022-2023

3. Learning Objectives
 recall and use the relationship
between the moment of a force and
its distance from the pivot:
Moment = force x perpendicular
distance form pivot
 recall that the weight of a body acts
through the centre gravity
 Define the torque of a couple

4. Moments
 Forces can make
objects turn if there is
a pivot.

5. The see-saw
 In order to make the seesaw turn
about its pivot, forces have to be
applied on either side of the plank

6. The see-saw
 What happens when
one person moves
closer to the fulcrum
or pivot?
 The turning effect of
the force is also
dependent on the
distance of the force
from the pivot.

7. Turning effect
 the turning effect is
called the moment
of force (or simply
"moment“)
 the distance is
called the moment
arm (or lever arm)
of the force.

8. Moment of a Force
 To work out a
moment, we need to
know two things:
 the force or weight
applied
 the distance from the
pivot that the force or
weight is applied.
 Force and distance
must be
perpendicular to each
other

9. Moment of a Force
 Product of force and the
perpendicular distance
 From the pivot

10. Moment and Equilibrium
 Conditions for Equilibrium
 Net force is zero
 Net moment is zero at any point

11. Example
 Find the force F that will balance the
seesaw.

12. Example
 Find the force F that will balance the
seesaw.

13. Center of gravity
 The centre of gravity of an object is
the point where the whole weight of
the object may be considered to act.

14. Center of gravity
 For a regularly-
shaped object, the
centre of gravity is
at its centre and,
where supported
there, it balances.

15. Example
 A uniform plank, 100 cm long and weighing
1.0 N is balanced at its midpoint by a
support. A weight of 1.20 N is hanged 5 cm
from the left end. It was found out that an
unknown weight W would balance the plank
if it is positioned 72 cm from the left end.
 What is the weight W of the object?
 How much force is exerted by the support on
the plank?

16. Couple
 Two parallel forces
equal in magnitude
 But opposite in
direction
 Has a turning
effect about a pivot
located midway
between them

17. Torque of a Couple
 Product of
 One of the forces
 And the distance between them

18. Thank You