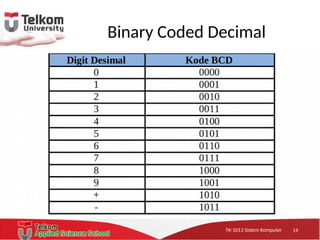
Dokumen tersebut membahas tentang representasi bilangan bertanda pada sistem komputer, yang mencakup empat teknik representasi bilangan bertanda yaitu sign magnitude, one's complement, two's complement, dan binary coded decimal. Dokumen ini juga menjelaskan operasi aritmatika pada masing-masing teknik representasi bilangan bertanda tersebut.