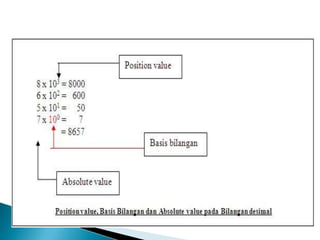
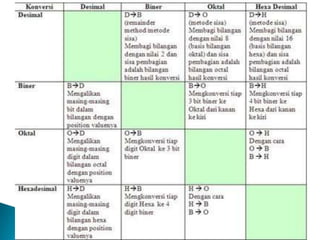
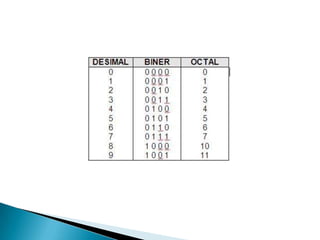
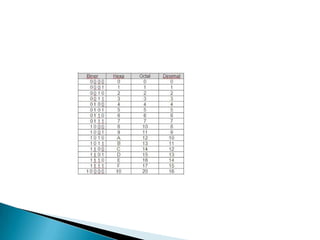
Dokumen ini menjelaskan dasar-dasar operasi komputer yang bergantung pada aliran listrik, dengan menyoroti sistem bilangan biner, desimal, oktal, dan heksadesimal. Kondisi on dan off pada komputer diwakili dengan 1 dan 0, dan data diolah menggunakan kombinasi kedua simbol tersebut. Selain itu, dokumen ini juga menguraikan proses konversi antara sistem bilangan serta penjumlahan dalam berbagai sistem numerik.

2.  Pada dasarnya, komputer baru bisa bekerja
kalau ada aliran listrik yang mengalir
didalamnya.
 Dalam hal ini, aliran listrik yang mengalir
ternyata memiliki dua kondisi, yaitu kondisi
ON yang berarti ada arus listrik, dan kondisi
OFF yang berarti tidak ada arus listrik.
 Berdasar hal tersebut kemudian dibuat
perjanjian, bahwa kondisi ON diberi lambang
1 (angka satu), dan kondisi OFF diberi
lambang 0 (angka nol).

3.  Seluruh data yang berupa angka, abjad
ataupun special character kemudian ditulis
dalam rangkaian kombinasi 0 dan 1, misal
angka 5 ditulis dalam bentuk 000101 dan
huruf D ditulis dalam 110100.
 Pabrik komputer membuat seluruh
terjemahan ini dalam bentuk rangkaian
elektronik yang tersimpan didalamnya.

4.  Ada beberapa sistem bilangan yang
digunakan dalam sistem digital. Yang paling
umum adalah sistem bilangan desimal, biner,
oktal dan heksadesimal
 Sistem bilangan desimal merupakan sistem
bilangan yang paling familier dengan kita
karena berbagai kemudahannya yang kita
pergunakan sehari – hari.

5.  basis/radix ,
 absolute digit dan
 positional value

7.  Bilangan dasar =
2(binary/biner),
8 (oktal) ,
10 (desimal) ,
16 (heksa desimal).

8. nilai mutlak dari masing-masing digit bilangan

9. Penimbang/bobot dari masing-masing digit
bilangan tergantung letak dan posisinya
Yaitu nilai basis di pangkatkan dengan urutan
posisinya.

11.  1. BINER (radiks / basis 2)
* Notasi : (n)2
* Simbol : angka 0 dan 1
2. OKTAL (radiks / basis 8)
* Notasi : (n)8
* Simbol : angka 0, 1, 2, 3, 4, 5, 6, 7
3. DESIMAL (radiks / basis 10)
* Notasi : (n)10
* Simbol : angka 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
4. HEKSADESIMAL (radiks / basis 16)
* Notasi : (n)16
* Simbol : angka 0,1,2,3,4,5,6,7,8,9,A,B, C,D,E,F

12.  Penjumlahan untuk angka desimal :
1) digit dari bilangan desimal ditambahkan
satu per satu dari kanan kekiri
2) Bila Hasil penjumlahan antar kolom
melebihi 9 maka hasil penjumlahan dikurangi
nilai 10. dan carry of dijumlahkan dengan
digit pada kolom sebelah kiri.

14.  Penjumlahan biner :
Penjumlahan dengan biner sama dengan penjumlahan
desimal :
Sistem bilangan desimal kurang serasi digunakan pada
sistem digital karena sulit untuk mendesain rangkaian
elektronik sedemikian rupa sehingga dapat bekerja
dengan 10 level tegangan yang berbeda ( 0 – 9 ).
Sebaliknya akan lebih mudah mendesain rangkaian
elektronik yang beroperasi dengan hanya menggunakan 2
level tegangan saja. Untuk alasan ini hampir semua sistem
digital menggunakan sistem bilangan biner ( dasar 2 )
sebagai dasar operasinya. Pada sistem biner hanya
digunakan dua simbol / nilai digit yang mungkin yakni : 0
dan 1.

16.  Ikuti langkah-langkah berikut ini :
1. Tuliskan bilangan biner dengan lengkap
2. Tulis deret bilangan : 1,2,4,8,16,32,64,
…..dst, di bawah bilangan biner
dimulai dari bit paling kanan (LSB )
3. Coret semua bilangan desimal yang
bertepatan dengan digit biner 0.
4. Jumlahkan seluruh bilangan desimal yang
masih tersisa .

18.  Dalam sistem digital selain bilangan biner
juga digunakan sistem bilangan octal, namun
sistem ini tidak dipakai dalam perhitungan
melainkan untuk memendekkan bilangan
biner saja. Bilangan octal dikenal dengan
sistem bilangan dasar delapan. Berikut
diberikan tabel yang memuat perbandingan
antara bilangan: Desimal,Biner dan Octal

20.  Konversi dilakukan dengan membagi delapan
bilangan desimal hingga bilangan desimal
habis dibagi dan sisanya dituliskan disebelah
kanannya ( seperti konversi desimal ke biner
).

21.  Proses perubahannya dilakukan dengan
mengelompokkan bilangan – bilangan biner
menjadi beberapa group , dimana setiap
group terdiri dari 3 bit biner dan dimulai dari
LSB.
Langkah berikutnya mengkonversi setiap
kelompok kedalam bentuk octal

23.  Sistem bilangan ini dikenal dengan basis
enam belas . Seperti halnya octal, hexa juga
dipergunakan untuk memendekkan
persamaan-persamaan bilangan biner.
Berikut tabel komparasi antara Biner , Octal
dan Hexa.

25.  Sistem operasi hexa desimal sama seperti
sistem bilangan yang lain.
Konversi Hexa ke Desimal
Konversi Hexa ke Desimal berlangsung sama
seperti bilangan yang lainnya,melainkan
menggunakan bilangan dasar 16.

27.  Konversi Desimal ke Hexa
Bilangan decimal dapat diubah kedalam
bentuk Hexa menggunakan pembagian
dengan factor pembagi 16. Hasilnya berupa
sisa yang diterjahkan kedalam bentuk hexa
yang dibaca dari bawah ke atas