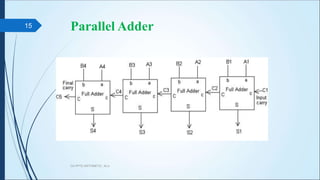
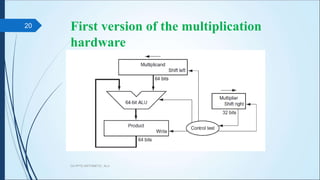
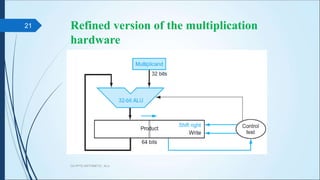
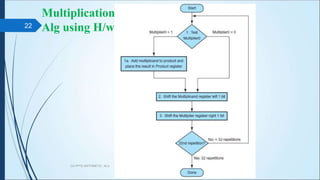
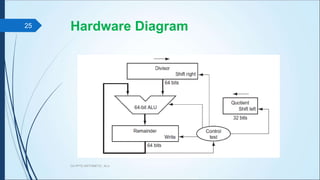
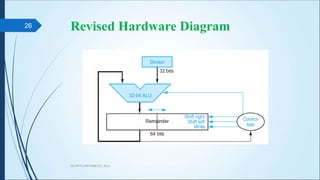
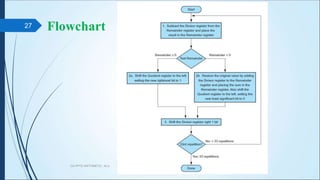
The document discusses arithmetic operations in computer architecture. It describes how the arithmetic logic unit (ALU) performs operations like addition, subtraction, multiplication and division on fixed-point and floating-point numbers. It explains different representations for integers like signed magnitude, one's complement and two's complement. Addition and subtraction are implemented using half adders, full adders and parallel adders. Multiplication is done by shifting and adding and division uses a repeated subtraction approach. Hardware designs for performing these operations are also presented.

1. COMPUTER ARCHITECTURE
UNIT – II ARITHMETIC OPERATIONS
CA PPT5 ARITHMETIC, ALU
1
ALU - Addition and subtraction – Multiplication – Division – Floating
Point operations – Subword parallelism

2. Arithmetic for Computers
 ALU - Arithmetic & Logic Unit
 Responsible for performing arithmetic operations such as addition,
subtraction, division and multiplication and logical operations such
as AND, OR and their inversion etc.,
 Arithmetic operations are performed on data type
Fixed point numbers
Floating point numbers
 Representing number in such data type is known as
Fixed point representation
Floating point representation
CA PPT5 ARITHMETIC, ALU
2

3. Fixed point representation
 Integer numbers
 2 forms
Signed integer (Negative number) -15
Unsigned integer (Positive number) 15
 Techniques used to represent integer numbers are
Signed Magnitude representation
1’s Complement
2’s Complement
CA PPT5 ARITHMETIC, ALU
3

4. Signed Magnitude representation
 There are many schemes for representing negative integers with
patterns of bits.
 One scheme is sign-magnitude
 It uses one bit (MSB) to indicate the sign.
 "0" indicates a positive integer, and "1" indicates a negative integer
 The rest of the bits are used for the magnitude of the number
 Example: -2410 is represented as
1001 1000
The sign "1" means negative
The magnitude is 24 (in 7-bit binary)
CA PPT5 ARITHMETIC, ALU
4

5. Example
 Decimal values of the following 8-bit sign-magnitude numbers
10000011 = -3
00000101 = +5
11111111 = ?
01111111 = ?
 Represent the following in 8-bit sign-magnitude
-15 = 10001111
+7 = 00000111
-1 = ?
CA PPT5 ARITHMETIC, ALU
5

6. One’s Complement
CA PPT5 ARITHMETIC, ALU
6
 Perform NOT operation
 Example find 1’s complement for 110101002

7. Two’s Complement
CA PPT5 ARITHMETIC, ALU
7
 2’s complement = 1’s complement + 1

8. Two’s Complement
1 1 0 0 0 1 0 0
¬ 0 0 1 1 1 0 1 1
+ 1
0 0 1 1 1 1 0 0
CA PPT5 ARITHMETIC, ALU
8
 2’s complement = 1’s complement + 1
 Example (11000100)2

9. Addition & Subtraction
Addition
 Rules for Binary Addition
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, and carry 1 to the next more significant bit
Example : Add 610 to 710 in binary
11
0110 (610)
+ 0111 (710)
------
1101  (1310)
CA PPT5 ARITHMETIC, ALU
9

10. Addition
 Logic circuit which perform addition of 2 bits is call half adder
 3 bits (2 significant bit & 1 Carry) is called full adder
Half Adder
Block Diagram Truth Table
i/p
o/p
CA PPT5 ARITHMETIC, ALU
10
Half
Adder
A B
S
C
A B S(um) C(arry)
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1

11. Karnaugh Map
Sum = A B ̅ + A ̅ B. Carry = AB
CA PPT5 ARITHMETIC, ALU
11
A
B
Sum
Carry
Logic Diagram

12. Full Adder
Block Diagram Truth Table
CA PPT5 ARITHMETIC, ALU
12
Full
Adder
A B
S
Cout
Carry In
(Cin)
Cin A B S(um) Cout
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

13. Karnaugh Map
S = A ̅ B ̅ Cin + A ̅ BC ̅ in + ABCin Cout = AB + ACin + BCin
CA PPT5 ARITHMETIC, ALU
13

14. Logic Diagram
CA PPT5 ARITHMETIC, ALU
14
Carry
Sum

15. Parallel Adder
CA PPT5 ARITHMETIC, ALU
15

16. Example – Addition (Base on MIPS)
CA PPT5 ARITHMETIC, ALU
16

17. Example – Subtraction (Base on MIPS)
CA PPT5 ARITHMETIC, ALU
17
Subtracting 6ten from 7ten can be done directly:

18. Binary Subtraction
 Suppose we want to perform A-B
 Steps:
 Take 2’s Complement of B
 Result  A + 2’s Complement of B
 If Carry is generated  Result is Positive (Ignore Carry)
 If no Carry  Result is Negative & in the 2’s Complement form
 Example : Perform (28)10 – (15)10 using 6 bit 2’s Complement
representation
CA PPT5 ARITHMETIC, ALU
18

19. Multiplication
 Multiplying 1000ten by 1001ten:
 The first operand is called the multiplicand
 the second the multiplier
 The final result is called the product
CA PPT5 ARITHMETIC, ALU
19

20. First version of the multiplication
hardware
CA PPT5 ARITHMETIC, ALU
20

21. Refined version of the multiplication
hardware
CA PPT5 ARITHMETIC, ALU
21

22. Multiplication
Alg using H/w
CA PPT5 ARITHMETIC, ALU
22

23. A Multiply Algorithm
 Using 4-bit numbers to save space, multiply 2ten x 3ten, or 0010two x 0011two.
CA PPT5 ARITHMETIC, ALU
23

24. Division Algorithm
CA PPT5 ARITHMETIC, ALU
24

25. Hardware Diagram
CA PPT5 ARITHMETIC, ALU
25

26. Revised Hardware Diagram
CA PPT5 ARITHMETIC, ALU
26

27. Flowchart
CA PPT5 ARITHMETIC, ALU
27

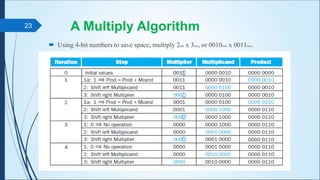
28. Example: Using a 4 bit version of the Algorithm
Divide 710 by 210 [0000 0111(2) by 0010(2)]
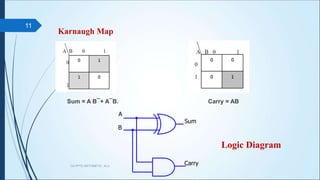
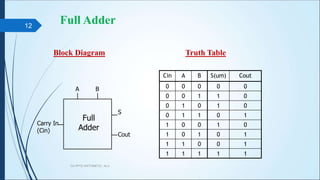
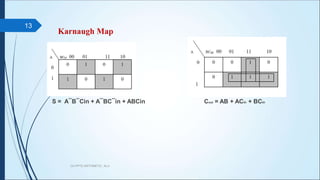
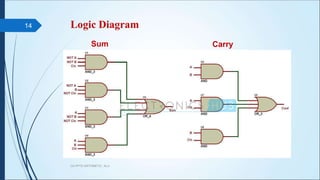
CA PPT5 ARITHMETIC, ALU
28