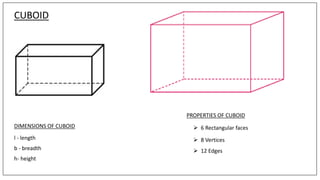
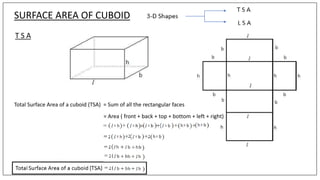
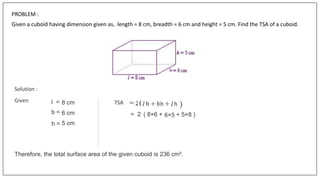
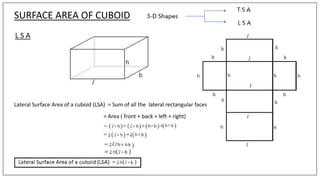
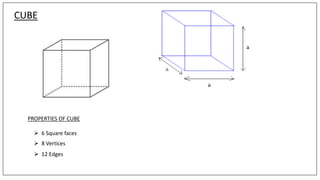
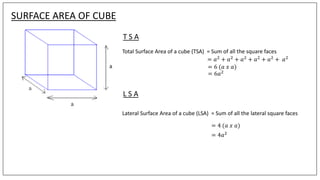
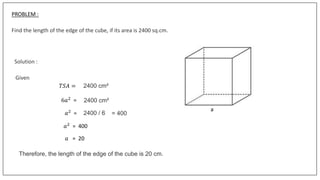
This document discusses the properties and formulas for calculating surface areas of cubes and cuboids. A cuboid has six rectangular faces, eight vertices and twelve edges. The total surface area of a cuboid is the sum of all rectangular faces. The lateral surface area excludes the top and bottom faces. A cube is a special type of cuboid where all dimensions are equal. It has six square faces, eight vertices and twelve edges. The total surface area of a cube is 6 times the area of one face (6a2) and the lateral surface area is 4 times the area of one face (4a2). Examples are provided to demonstrate calculating surface areas using given dimensions.

3. CUBE CUBOID SPHERE CONE CYLINDER

4. CUBE CUBOID

5. CUBOID
 6 Rectangular faces
 8 Vertices
 12 Edges
PROPERTIES OF CUBOID
l - length
b - breadth
h- height
DIMENSIONS OF CUBOID

6. SURFACE AREA OF CUBOID
T S A
Total Surface Area of a cuboid (TSA) = Sum of all the rectangular faces
= Area ( front + back + top + bottom + left + right)

7. PROBLEM :
Given a cuboid having dimension given as, length = 8 cm, breadth = 6 cm and height = 5 cm. Find the TSA of a cuboid.
TSA
Solution :
Given l =
b =
h =
= 2
Therefore, the total surface area of the given cuboid is 236 cm².
8 cm
6 cm
5 cm
( 8×6 + 6×5 + 5×8 )

8. SURFACE AREA OF CUBOID
L S A
Lateral Surface Area of a cuboid (LSA) = Sum of all the lateral rectangular faces
= Area ( front + back + left + right)

9. CUBE
 6 Square faces
 8 Vertices
 12 Edges
PROPERTIES OF CUBE

10. SURFACE AREA OF CUBE
Total Surface Area of a cube (TSA) = Sum of all the square faces
T S A
= 6𝑎2
= 6 (𝑎 𝑥 𝑎)
L S A
Lateral Surface Area of a cube (LSA) = Sum of all the lateral square faces
= 4 (𝑎 𝑥 𝑎)
= 4𝑎2
= 𝑎2
+ 𝑎2
+ 𝑎2
+ 𝑎2
+ 𝑎2
+ 𝑎2

11. PROBLEM :
Find the length of the edge of the cube, if its area is 2400 sq.cm.
Solution :
Given
6𝑎2
=
𝑇𝑆𝐴 = 2400 cm²
2400 cm²
𝑎2 = 2400 / 6 = 400
𝑎2
= 400
𝑎 = 20
Therefore, the length of the edge of the cube is 20 cm.
a

12. SUMMARY :
CUBOID :
 Properties :
 6 Rectangular Faces
 8 Vertices
 12 Edges
 Surface area
 x

CUBE :
 Cube is a cuboid with all its dimensions equal.
 Properties :
 6 Square Faces
 8 Vertices
 12 Edges
 Surface area
 TSA = 6𝑎2
 LSA = 4𝑎2