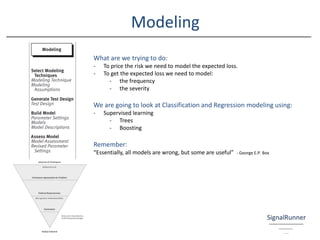
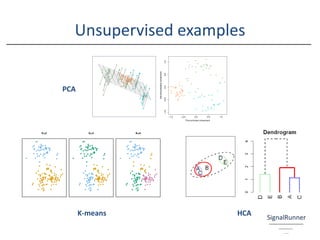
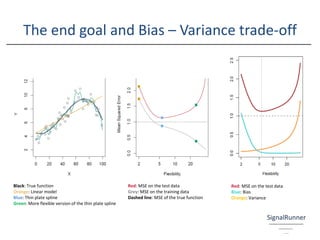
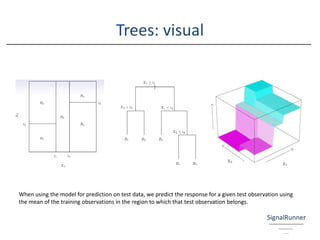
The document provides an introductory overview of the application of machine learning in insurance, emphasizing the importance of data science and various modeling techniques such as supervised and unsupervised learning. It discusses concepts like classification, regression, and the use of decision trees and boosting in modeling, along with the associated challenges such as the bias-variance trade-off. Additionally, it highlights the significance of understanding the holistic skill set required for effective data science roles in the insurance industry.

1. Applied Machine Learning Intro
Insurance
Gregg Barrett I Partner I SignalRunner

2. Disclosure
This is a paid for engagement.
This is not a marketing engagement.
Where reference is made to third party products and services it is merely for illustrative purposes
and should not be viewed as an endorsement of any kind unless stated so.
The intent of this engagement is to build a better understanding of the application of machine
learning in insurance. To this end the engagement should be viewed as introductory.
Should you have any questions or require any further information please contact us at:
enquire@signalrunner.net
Biographical information of the presenter can be found at:
http://www.linkedin.com/in/greggbarrett

3. Resources
An Introduction to Statistical Learning with
Applications in R
The Elements of Statistical Learning Computer Age Statistical Inference

4. Outline
- Where we are
- A reminder
- Modeling
- Techniques
- Unsupervised examples
- Parametric and Non-parametric
- The end goal
- The end goal and Bias – Variance trade-off
- Trees
- intro
- visual
- linear vs non-linear
- advantages
- Boosting with trees
- tuning parameters
- strengths
- relative influence
- partial dependence plots
- bits and bobs
- Reference
- Slide notes

5. Where we are
Value Proposition:
You should understand the importance of Data Science in insurance and be familiar with the
value proposition. [1]
Strategy:
The Data Science strategy covering people, process and technology is being executed.
Now:
The application of a machine learning approach to classification and regression.
[1] A report on the value proposition of analytics in P&C insurance
https://1drv.ms/b/s!AnGNabcctTWNhC7AE6hW_qtJar9i

6. “People learn a bunch of python and they call it a day and say, ‘Now I’m a data scientist.’ They’re not, there’s a big difference,”
“That’s what employers need to be more cognizant of. You need to hire people that have this holistic skill set that’s effective at solving
business problems.” [2]
Vasant Dhar
Professor, Stern School of Business and Center for Data Science at New York University
Founder of SCT Capital Management
[2] New Breed of Super Quants at NYU Prep for Wall Street: https://bloom.bg/2xfvN65
A reminder
The application of
modeling techniques
is not done in
isolation.

7. What are we trying to do:
- To price the risk we need to model the expected loss.
- To get the expected loss we need to model:
- the frequency
- the severity
We are going to look at Classification and Regression modeling using:
- Supervised learning
- Trees
- Boosting
Remember:
“Essentially, all models are wrong, but some are useful” - George E.P. Box
Modeling

8. Supervised Learning:
In supervised learning there is a response (dependent) variable.
Unsupervised learning:
In unsupervised learning there is no response (dependent) variable.
Classification examples Regression examples
- Logistic Regression
- Linear Discriminant Analysis
- Quadratic Discriminant Analysis
- K-nearest neighbours
- General Additive Models
- Random Forests
- Boosting
- Support Vector Machines
- Deep Learning
- Least Squares
- Ridge Regression
- Lasso
- Support Vector Machine
- Random Forests
- Boosting
- Support Vector Machines
- General Additive Models
- Principle Components Regression
- Deep Learning
Unsupervised examples
- Principle Component Analysis
- K-means Clustering
- Hierarchical Clustering
- Self-organizing maps
- Independent Components Analysis
- Spectral Clustering
Techniques

9. PCA
K-means HCA
Unsupervised examples

10. Parametric and Non-parametric
Parametric:
Parametric methods involve a two-step model-based approach.
1. First, we make an assumption about the functional form, or shape, off.
2. After a model has been selected, the problem is now one of estimating the parameters - we need a
procedure that uses the training data to fit or train the model.
Parametric modeling therefore reduces the problem of estimating f down to one of estimating a set of
parameters.
Non-parametric:
Non-parametric means that we do not make explicit assumptions about the functional form of f. Where the
intent is to find a function መ𝑓 such that Y ≈ መ𝑓(X) for any observation (X, Y).

11. The end goal
For prediction -> of interest is the prediction error
For regression the prediction error. Example is the MSE.
For classification the prediction error is the misclassification error rate.
For estimation -> of interest is the accuracy of a function
Can be thought of as estimating the true regression surface.
sⅆ 𝑥 = sⅆ ȁ෤𝑦 𝑥
For explanation -> use of more elaborate inferential tools
The relative contribution of the different predictors is of interest. How the regression surface is composed
is of prime concern in this use.

12. The end goal and Bias – Variance trade-off
Black: True function
Orange: Linear model
Blue: Thin plate spline
Green: More flexible version of the thin plate spline
Red: MSE on the test data
Grey: MSE on the training data
Dashed line: MSE of the true function
Red: MSE on the test data
Blue: Bias
Orange: Variance

13. Trees: intro
- These involve stratifying or segmenting the predictor space into a number of
simple regions.
- Since the set of splitting rules used to segment the predictor space can be
summarized in a tree, these types of approaches are known as decision-tree
methods.
Fitting trees for regression:
- Splitting rule example is the RSS
Fitting trees for classification:
- Splitting rule example is the Gini index also referred to as a measure of node purity. A small
value indicates that a node contains predominantly observations from a single class.

14. When using the model for prediction on test data, we predict the response for a given test observation using
the mean of the training observations in the region to which that test observation belongs.
Trees: visual

15. Trees: linear vs non-linear
- True linear boundary
- Linear model
- True non-linear boundary
- Linear model
- True linear boundary
- Tree based model
- True non-linear boundary
- Tree based model

16. Trees: advantages
- Trees are easy to explain.
- Trees can be displayed graphically easing interpretation.
- Trees handle qualitative predictors without the need to create dummy
variables.

17. Boosting with trees
- Unlike fitting a single large tree to the data, which potentially leads to over fitting,
the boosting approach instead learns slowly.
- Given the current model, we fit a tree to the residuals from the model. We then
add this new tree into the fitted function in order to update the residuals.
- Each of these trees can be rather small, with just a few terminal nodes,
determined by a parameter in the algorithm.
- By fitting small trees to the residuals, we slowly improve the fit in areas where it
does not perform well.

18. Boosting with trees: tuning parameters
Shrinkage (the learning rate)
In boosting the construction of each tree depends on the trees that have already been grown. Typical values
are 0.01 or 0.001, and the right choice can depend on the problem.
Number of trees (the number of iterations)
Cross-validation and information criterion can be used to select the number of trees.
Boosting can overfit if the number of trees is too large, although this overfitting tends to occur slowly
Depth (interaction depth)
Depth sets the number of splits in each tree, which controls the complexity of the boosted ensemble.

19. Boosting with trees: strengths
- Single depth trees are understandable and interpretable
- Variable importance measure
For example, the total amount that the RSS is decreased due to splits over a given
predictor, averaged over all trees. A large value indicates an important predictor.
- Tree-based methods are non-parametric universal approximators
With sufficient complexity, a tree can represent any continuous function with an
arbitrary high precision
- Require very little data pre-processing
Trees handle the predictor and response variables of any type without the need
for transformation, and are insensitive to outliers and missing values.

20. Boosting with trees: relative influence
Variable Relative Influence
NVCat 16.3596783
Blind_Submodel_Group 14.2303008
Cat1 6.5404562
Cat11 5.7539849
Var8 5.5884656
Cat12 5.3796950
Blind_Model_Group 4.7973538
Var6 4.4931525
Var7 3.6582142
NVVar2 3.6574831
Var5 3.5106614
Cat3 2.9454841
Var2 2.6266979
Var3 2.5477424
Var1 2.4460909
Vehicle_Age 2.4109539
Var4 1.9133120
Cat6 1.8431855
Cat10 1.7352951
NVVar4 1.4868086
Cat2 1.3424942
NVVar1 1.2158919
OrdCat 1.1734845
NVVar3 1.0518956
Cat8 0.6792301
Blind_Make_Group 0.6119876

21. Boosting with trees: partial dependence plots
Partial dependence of the log-odds of
spam vs. email as a function of joint
frequencies of hp and the character !

22. Boosting with trees: bits and bobs
Loss function examples in ‘mboost’:

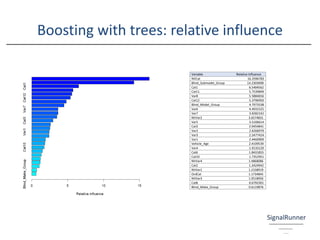
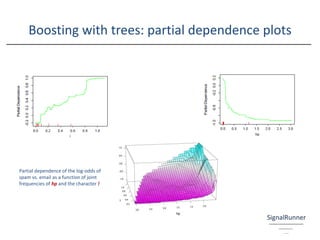
23. Boosting with trees: bits and bobs
Stopping criteria for the number of trees (the number of iterations)
Various possibilities to determine the stopping iteration exist. AIC is usually not recommended as AIC-based
stopping tends to overshoot the optimal stopping dramatically. (Hofner, Mayr, Robinzonovz, Schmid, 2014)
Feature selection:
Randomised feature selection combined with backward elimination (also called recursive feature elimination)
where the least important variables are removed until out-of-bag prediction accuracy drops [3]
R Packages for boosting with trees:
XGBoost
https://cran.r-project.org/web/packages/xgboost/vignettes/xgboostPresentation.html
mboost
https://cran.r-project.org/web/packages/mboost/index.html
gbm
https://cran.r-project.org/web/packages/gbm/index.html
[3] Feature selection for ranking using boosted trees
http://bit.ly/2gukenW

24. Reference
Slide 5, 6:
CRISP-DM. (2000). Generic tasks (bold) and outputs (italic) of the CRISP-DM reference model. (figure). Retrieved from CRISP-DM. (2000). CRISP-DM 1.0. [pdf]. Retrieved from https://the-
modeling-agency.com/crisp-dm.pdf
Slide 8, 11, 13, 14, 27:
James, G., Witten, D., Hastie, T., Tibshirani, R. (2013). Introduction to statistical learning with applications in R. [ebook]. Retrieved from
http://www-bcf.usc.edu/~gareth/ISL/getbook.html
Slide 20:
Hastie, T., Tibshirani, R., and Friedman, J. (2009). The elements of statistical learning. data mining, inference, and prediction. Second edition. Springer Series in Statistics.
Springer. Retrieved from https://web.stanford.edu/~hastie/Papers/ESLII.pdf
Slide 21, 28:
Hofner, B., Mayr, A., Robinzonovz, N., Schmid, M. (2014). An overview on the currently implemented families in mboost. [table]. Retrieved from Hofner, B., Mayr, A., Robinzonovz, N., Schmid,
M. (2014). Model-based boosting in r: a hands-on tutorial using the r package mboost. [pdf]. Retrieved from https://cran.r-project.org/web/packages/mboost/vignettes/mboost_tutorial.pdf
Slide 22:
Hofner, B., Mayr, A., Robinzonovz, N., Schmid, M. (2014). Model-based boosting in r: a hands-on tutorial using the r package mboost. [pdf]. Retrieved from https://cran.r-
project.org/web/packages/mboost/vignettes/mboost_tutorial.pdf
Slide 25, 26:
Natekin, A., Knoll, A. (2013). Gradient boosting machines tutorial. [pdf]. Retrieved from http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3885826/
Slide 26:
Yang, Y., Qian, W., Zou, H. (2014). A boosted nonparametric tweedie model for insurance premium. [pdf]. Retrieved from https://people.rit.edu/wxqsma/papers/paper4
Slide 27:
Ridgeway, G. (2012). Generalized boosted models: a guide to the gbm package. [pdf]. Retrieved from https://cran.r-project.org/web/packages/gbm/gbm.pdf
Slide 28:
Geurts, P., Irrthum, A., Wehenkel, L. (2009). Supervised learning with decision tree-based methods in computational and systems biology. [pdf]. Retrieved from
http://www.montefiore.ulg.ac.be/~geurts/Papers/geurts09-molecularbiosystems.pdf

25. Slide 7:
Supervised learning:
Supervised learning refers to the subset of machine learning methods which derive models in the form of input-output relationships. More precisely, the
goal of supervised learning is to identify a mapping from some input variables to some output variables on the sole basis of a given sample of joint
observations of the values of these variables.
Slide 8:
PCA:
PCA looks for a low-dimensional representation of the observations that explains a good fraction of the variance.
The first principal component loading vector has a very special property: it denes the line in p-dimensional space that is closest to the n observations (using
average squared Euclidean distance as a measure of closeness).
The notion of principal components as the dimensions that are closest to the n observations extends beyond just the first principal component.
For instance, the first two principal components of a data set span the plane that is closest to the n observations, in terms of average squared Euclidean
distance.
K-means:
The idea behind K-means clustering is that a good clustering is one for which the within-cluster variation is as small as possible.
We want to partition the observations into K clusters such that the total within-cluster variation, summed over all K clusters, is as small as possible. Within
cluster variation is typically defined in terms of Euclidean distance.
Hierarchical Clustering Algorithm:
- Start with each point in its own cluster.
- Identify the closest two clusters and merge them.
- Repeat.
- Ends when all points are in a single cluster.
Slide notes

26. Slide 9:
If in step one we selected the functional form as being a linear model of the form:
Y ≈ β0 + β1X1 + β2X2 + . . . + βpXp.
In step 2 we could use ordinary least squares to estimate the model parameters.
Note: “Nonparametric” is another name for “very highly parameterized.” (Parameterized to the data)
Slide 11:
Points are simulated data points with error, from the true function in black
Slide 12:
Base learner:
Boosted models can be implemented with different base-learner functions. Common base-learner functions include; linear models, smooth models,
decision trees, and custom base-learner functions.
Several classes of base-learner models can be implemented in one boosted model. This means that the same functional formula can include both smooth
additive components and the decision trees components at the same time. (Natekin, Knoll, 2013).
Slide notes

27. Slide 16:
Boosting:
Given an initial model (decision tree), we fit a decision tree (the base-learner) to the residuals from the initial model. That is, we fit a tree using the current
residuals, rather than the outcome Y. We then add this new decision tree into the fitted function in order to update the residuals. The process is conducted
sequentially so that at each particular iteration, a new weak, base-learner model is trained with respect to the error of the whole ensemble learnt so far.
With such an approach the model structure is thus learned from data and not predetermined, thereby avoiding an explicit model specification, and
incorporating complex and higher order interactions to reduce the potential modelling bias. (Yang, Qian, Zou, 2014).
This flexibility makes the boosting highly customizable to any particular data-driven task. It introduces a lot of freedom into the model design thus making
the choice of the most appropriate loss function a matter of trial and error. (Natekin, Knoll, 2013).
A careful specification of the loss function leads to the estimation of any desired characteristic of the conditional distribution of the response. This coupled
with the large number of base learners guarantees a rich set of models that can be addressed by boosting. (Hofner, Mayr, Robinzonovz, Schmid, 2014)
Slide notes

28. Slide 17:
Shrinkage (the learning rate):
The shrinkage parameter sets the learning rate of the base-learner models. In general, statistical learning approaches that learn slowly tend to perform well.
In boosting the construction of each tree depends on the trees that have already been grown. Typical values are 0.01 or 0.001, and the right choice can
depend on the problem. (Ridgeway, 2012). It is important to know that smaller values of shrinkage (almost) always give improved predictive performance.
However, there are computational costs, both storage and CPU time, associated with setting shrinkage to be low. The model with shrinkage=0.001 will likely
require ten times as many trees as the model with shrinkage=0.01, increasing storage and computation time by a factor of 10.
It is generally the case that for small shrinkage parameters, 0.001 for example, there is a fairly long plateau in which predictive performance is at its best. A
recommended rule of thumb is to set shrinkage as small as possible while still being able to fit the model in a reasonable amount of time and storage.
(Ridgeway, 2012).
Number of trees (the number of iterations):
Boosting can overfit if the number of trees is too large, although this overfitting tends to occur slowly if at all. (James, Witten, Hastie, Tibshirani, 2013).
Cross-validation and information criterion can be used to select the number of trees. Again it is worth stressing that the optimal number of trees and the
shrinkage (learning rate) depend on each other, although slower learning rates do not necessarily scale the number of optimal trees. That is, when
shrinkage = 0.1 and the optimal number of tress = 100, does not necessarily imply that when shrinkage = 0.01 the optimal number of trees = 1000.
(Ridgeway, 2012).
Depth (interaction depth):
Depth sets the number of splits in each tree, which controls the complexity of the boosted ensemble. When depth = 1 each tree is a stump, consisting of a
single split. In this case, the boosted ensemble is fitting an additive model, since each term involves only a single variable. More generally depth is the
interaction depth, and controls the interaction order of the boosted model, since d splits can involve at most d variables. (James, Witten, Hastie, Tibshirani,
2013).
Slide notes

29. Slide 18:
A strength of tree based methods is that single depth tress are readily understandable and interpretable.
Decision trees have the ability to select or rank the attributes according to their relevance for predicting the output, a feature that is shared with almost no
other non-parametric methods. (Geurts, Irrthum, Wehenkel, 2009).
From the point of view of their statistical properties, tree-based methods are non-parametric universal approximators, meaning that, with sufficient
complexity, a tree can represent any continuous function with an arbitrary high precision. When used with numerical attributes, they are invariant with
respect to monotone transformations of the input attributes. (Geurts, Irrthum, Wehenkel, 2009).
Importantly boosted decision trees require very little data pre-processing, which can easily be one of the most time consuming activities in a project of this
nature. As boosted decision trees handle the predictor and response variables of any type without the need for transformation, and are insensitive to
outliers and missing values, it is natural choice not only for this project but for insurance in general where there are frequently a large number of categorical
and numerical predictors, non-linearities and complex interactions, as well as missing values that all need to be modelled.
Slide 21:
An overview on the currently implemented families in mboost.
A careful specification of the loss function leads to the estimation of any desired characteristic of the conditional distribution of the response. This coupled
with the large number of base learners guarantees a rich set of models that can be addressed by boosting. (Hofner, Mayr, Robinzonovz, Schmid, 2014)
Slide 22:
Optimal number of iterations using AIC:
To maximise predictive power and to prevent overfitting it is important that the optimal stopping iteration is carefully chosen. Various possibilities to
determine the stopping iteration exist. AIC was considered however this is usually not recommended as AIC-based stopping tends to overshoot the optimal
stopping dramatically. (Hofner, Mayr, Robinzonovz, Schmid, 2014)
Relative influence assessment
One approach is to use backward elimination (also called recursive feature elimination) where the least important
variables are removed until out-of-bag prediction accuracy drops. This can be combined with a
randomised feature selection approach.
Slide notes