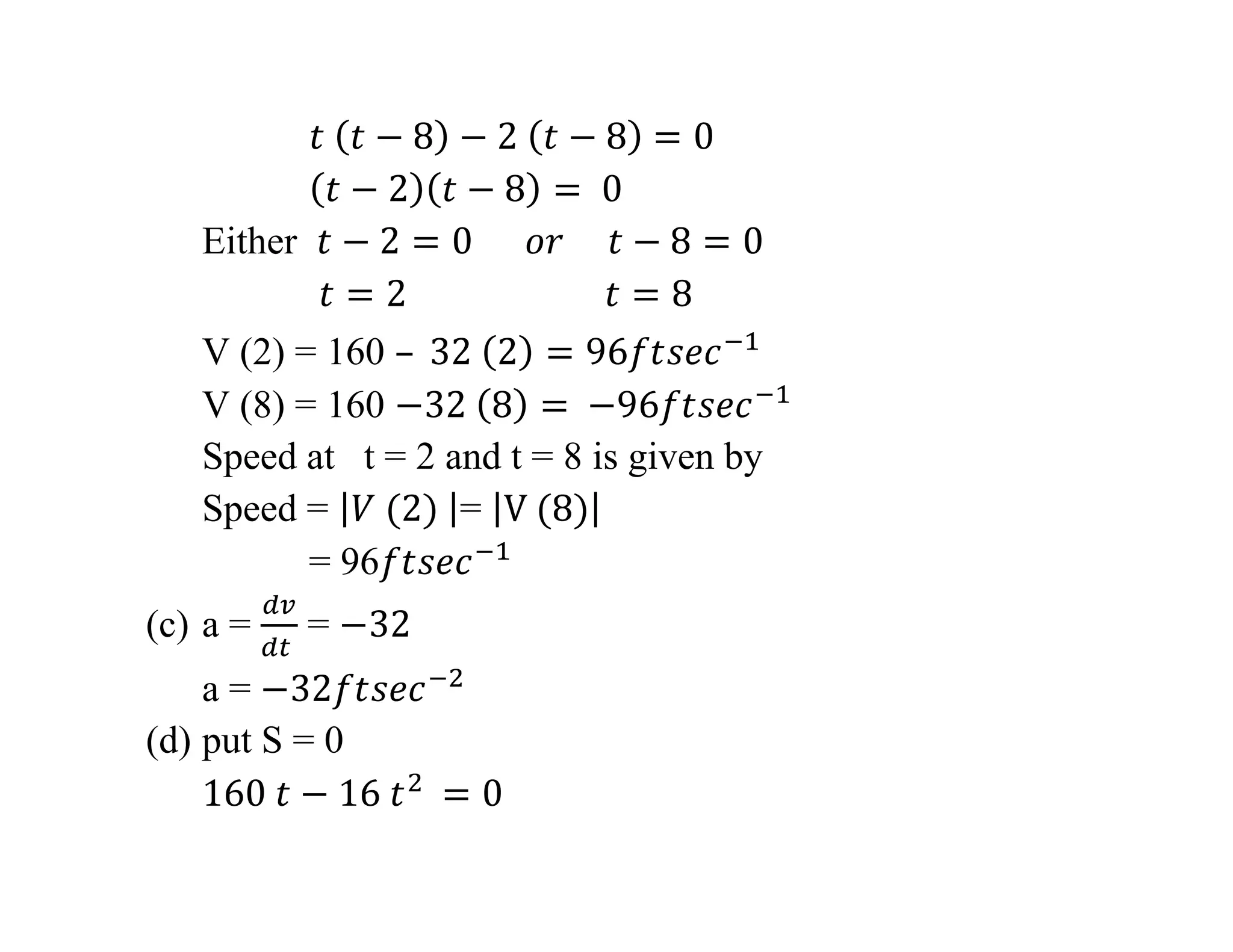The document discusses the physical meanings of derivatives, explaining average and instantaneous rates of change using calculus concepts. It includes various examples related to free fall, projectile motion, and marginal analysis in business, illustrating how derivatives apply to real-world situations. Additionally, it examines body motion on a coordinate line, calculating displacement, velocity, and changes in direction.

1. Applied Calculus
1st
Semester
Lecture -06
Muhammad Rafiq
Assistant Professor
University of Central Punjab
Lahore Pakistan

2. PHYSICAL MEANINGS OF DERIVATIVE
Definition: The average rate of change of a function f(x) with
respect to ‘x’ over the interval from ° to ° is given by:
Average rate of change ° °
Definition: The instantaneous rate of change of ‘f’ with respect
to ‘x’ is given by:
Instantaneous rate of change at °
° °
Conclusion: Physically, derivative measures the instantaneous
rate of change of a function with respect to some independent
variable.

3. Note: We often use the word rate of change instead of
instantaneous rate of change.
EXAMPLE NO 1
The free fall motion of a heavy ball released from rest at
t = 0 is given by:
S = 4.9
(a) How many meters do the ball fall in first 2 seconds?
(b) What are its velocity, speed and acceleration then?
Solution:
S = 4.9
(a) The ball falls in first 2 seconds :

4. S (2) = 4.9 ( =19.8 m
(b) The velocity and acceleration is given by:
V (t) = = 9.8 t
At t = 2
V (2) = 9.8 (2) = 19.6
a= = 9.8
Speed = = 19.6
EXAMPLE NO 2
A dynamite blast a heavy rock straight up with a launch velocity
of 160 , it reaches a height of S = 160 t 16 feet
after‘t’ seconds.

5. (a) How high does the rock go?
(b) What is the velocity and speed of the rock when it is 256ft
above the ground on the way up on the way down?
(c) What is the acceleration of the rock at any time‘t’ during
its flight after the blast?
(d) When does the rock hit the ground?
Solution:
(a)
For maximum height
32 t = 160

6. Maximum height is given by
(b) Put S = 256
Then 256 = 160
16
16 (

7. Either
V (2) = 160
V (8) = 160
Speed at t = 2 and t = 8 is given by
Speed = =
= 96
(c) a = =
a =
(d) put S = 0

8. ,
,
At t = 0 the blast occur and at t = 10 the
rock hits the ground again.
Marginal Analysis:
(Application of derivative in business and economics)
The marginal cost at some level of production ‘x’ is the cost of
producing item.
The marginal cost can be approximated by taking derivative of
cost function.

9. EXAMPLE NO 3
The cost C(x) of producing ‘x’ units of some items is given by
(a)Find the actual cost of producing unit.
(b)Find the marginal cost when x = 1000
Solution:
(a)The actual cost of producing unit is
=
=
= 1.7999

10. (a) The marginal cost is given by
(1000)=2
=1.80
Conclusion:
(a) Part a is the average rate of change of cost function over
the interval 1000 to 1001
(b) Part b is the instantaneous rate of change of c(x) at x 1000
, thus the marginal cost at x 1000 is approximately equal
to the actual cost of producing units

11. EXAMPLE NO 4
Given the position, , of a body
moving on a coordinate line for , with ‘s’ in meters
and ‘t’ in seconds
a) Find the body’s displacement and average velocity for
the given time interval.
b) Find the body’s speed and acceleration at the endpoints
of the interval.
c) When in the interval does the body change direction (if
ever)?
Solution:
(a) S= ,

12. Displacement=
=
b) v =
v (0)=2(0)
= and
a= 2
a (0) =2
a (2) =2

13. ( c)
v=0 2t-3=0
t=3/2
‘v’ is negative in the interval 0<t<3/2 and ‘v’ is positive when
3/2 <t<2
the body changes direction at t=3/2
EXERCISE 2.3
Q(1-16)