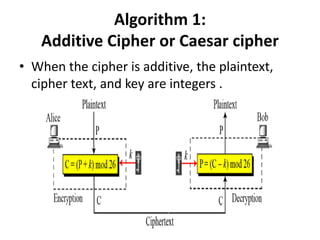
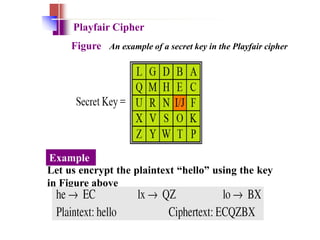
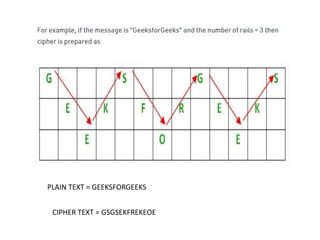
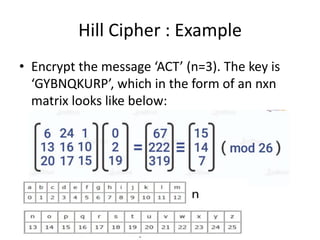
Classical encryption techniques include substitution ciphers like the Caesar cipher where letters are replaced, and transposition ciphers like the Rail Fence cipher where the order of letters is changed. The Playfair cipher is a substitution cipher that encrypts digrams (pairs of letters) based on a 5x5 key matrix. The Hill cipher is a polygraphic substitution cipher that encrypts blocks of letters using matrix multiplication modulo 26.

1. Classical Encryption
Techniques
TCS 419 : Unit 1

2. Classical cryptography
• Classical cryptography is based on the
mathematics and it relies on the
computational difficulty of factorizing large
number.
• In cryptography, a classical cipher is a type of
cipher that was used historically but for the
most part, has fallen into disuse.
• In contrast to modern cryptographic
algorithms, most classical ciphers can be
practically computed and solved by hand

4. Types of Classical Encryption
Techniques
We will study first the two popular types of
classical encryption
1. Substitution
2. Transposition.

5. Classical Substitution Ciphers
• Where letters of plaintext are
replaced by other letters or by
numbers or symbols
• Or if plaintext is viewed as a
sequence of bits, then substitution
involves replacing plaintext bit
patterns with ciphertext bit patterns

6. Caesar Cipher
• Earliest known substitution cipher
• By Julius Caesar
• First attested use in military affairs
• Replaces each letter by 3rd letter on
• Example:
meet me after the toga party
PHHW PH DIWHU WKH WRJD SDUWB

7. • When the cipher is additive, the plaintext,
cipher text, and key are integers .
Algorithm 1:
Additive Cipher or Caesar cipher

10. Brute-Force Attack
• During the brute-force attack, the intruder tries all
possible keys (or passwords), and checks which one of
them returns the correct plaintext. A brute-force attack
is also called an exhaustive key search.
• An amount of time that is necessary to break a cipher
is proportional to the size of the secret key.
The maximum number of attempts is equal to 2key size,
where key size is the number of bits in the key.
• Nowadays, it is possible to break a cipher with around
60-bit long key, by using the brute-force attack in less
than one day

11. Cryptanalysis of Caesar Cipher
• Only have 26 possible ciphers
–A maps to A,B,..Z
• Could simply try each in turn
• A brute force search
• Given ciphertext, just try all shifts of
letters
• Do need to recognize when have
plaintext

12. Playfair Cipher
• Not even the large number of keys in a
Ceasar cipher provides security
• One approach to improving security was
to encrypt multiple letters
• The Playfair cipher is an example
• Invented by Charles Wheatstone in 1854,
but named after his friend Baron Playfair

13. Playfair Key Matrix
• A 5X5 matrix of letters based on a
keyword
• Fill in letters of keyword (sans duplicates)
• Fill rest of matrix with other letters
• e.g. Using the keyword MONARCHY
M O N A R
C H Y B D
E F G I/J K
L P Q S T
U V W X Z

14. Playfair Cipher
Figure An example of a secret key in the Playfair cipher
Let us encrypt the plaintext “hello” using the key
in Figure above
Example

15. Playfair ciphers
• Matrix-based block
cipher
• In a 5x5 matrix, write
the letters of the
word “playfair” (for
example) without
dups, and fill in with
other letters of the
alphabet, except I,J
used
interchangeably.
















z
x
w
v
u
t
s
q
o
n
m
k
h
g
e
d
c
b
r
i
f
y
a
l
p

16. Playfair encryption
1. Break plaintext into letter
pairs
– If a pair would contain double
letters, split with x
– Pad end with x
– hellothere becomes…
– he lx lo th er ex
2. For each pair,
– If they are in the same row,
replace each with the letter to
its right (mod 5)
• he  KG
– If they are in the same column,
replace each with the letter
below it (mod 5)
• lo  RV
– Otherwise, replace each with
letter we’d get if we swapped
their column indices
• lx YV
He lx lo th er ex
KG YV RV QM GI KU
















z
x
w
v
u
t
s
q
o
n
m
k
h
g
e
d
c
b
r
i
f
y
a
l
p

19. Encrypting and Decrypting
Plaintext is encrypted two letters at a time
1. If a pair is a repeated letter, insert filler like 'X’
2. If both letters fall in the same row, replace each
with letter to right (wrapping back to start from
end)
3. If both letters fall in the same column, replace
each with the letter below it (again wrapping to
top from bottom)
4. Otherwise each letter is replaced by the letter in
the same row and in the column of the other
letter of the pair

20. Security of Playfair Cipher
• Security much improved over monoalphabetic
• Since have 26 x 26 = 676 digrams
• Would need a 676 entry frequency table to
analyse (verses 26 for a monoalphabetic)
• And correspondingly more ciphertext
• Was widely used for many years
–e.g. By US & British military in WW1
• It can be broken, given a few hundred letters
• Since still has much of plaintext structure

21. Transposition :Rail Fence
cipher
 write message letters out
diagonally over a number of rows
 then read off cipher row by row
 eg. write message out as:
Welcome to gehu
 giving ciphertext
WLOEOEUECMTGH
W L O E O E U
--------------------------------
E C M T G H

22. 3.22
Keyless Transposition Ciphers
Simple transposition ciphers, which were used in
the past, are keyless.
A good example of a keyless cipher using the first
method is the Rail Fence Cipher. The ciphertext
is created reading the pattern row by row. For
example, to send the message “Meet me at the
park”
Example
She then creates the ciphertext
“MEMATEAKETETHPR”.

23. PLAIN TEXT = GEEKSFORGEEKS
CIPHER TEXT = GSGSEKFREKEOE

25. Row Transposition Ciphers
 Is a more complex transposition
 write letters of message out in rows
over a specified number of columns
 then reorder the columns according
to some key before reading off the
rows
Key: 4312567
Column Out 4 3 1 2 5 6 7
Plaintext: a t t a c k p
o s t p o n e
d u n t i l t
w o a m x y z
Cipher text:
TTNAAPTMTSUOAODWCOIXKNLYPETZ

27. HILL CIPHER
• Hill cipher is a polygraphic substitution cipher based on
linear algebra.
• Each letter is represented by a number modulo 26. Often
the simple scheme A = 0, B = 1, …, Z = 25 is used, but this is
not an essential feature of the cipher.
• To encrypt a message, each block of n letters (considered as
an n-component vector) is multiplied by an invertible n × n
matrix, against modulus 26.
• To decrypt the message, each block is multiplied by the
inverse of the matrix used for encryption.
The matrix used for encryption is the cipher key, and it
should be chosen randomly from the set of invertible n × n
matrices (modulo 26).

28. Hill Cipher : Example
• Encrypt the message ‘ACT’ (n=3). The key is
‘GYBNQKURP’, which in the form of an nxn
matrix looks like below: