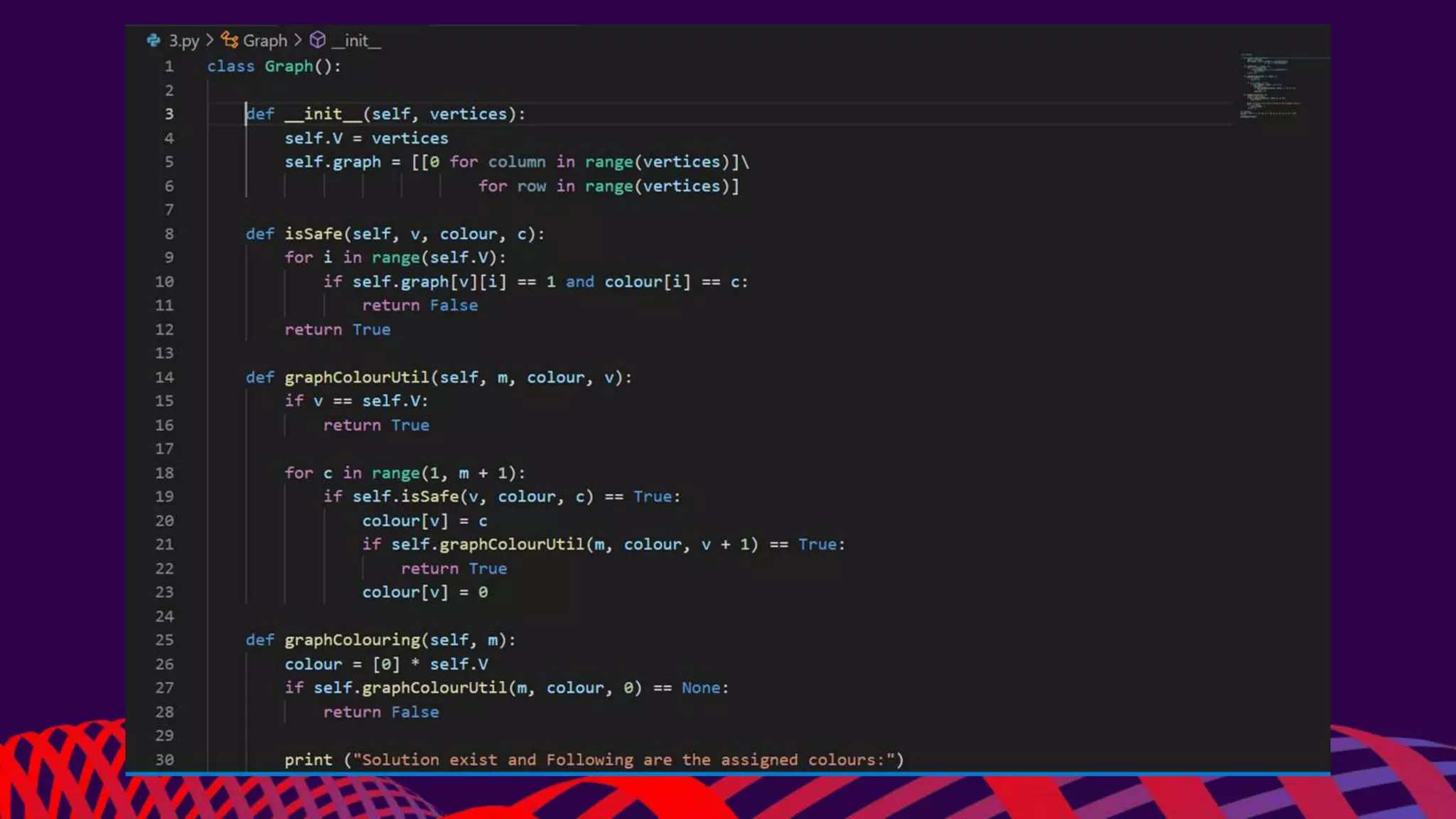
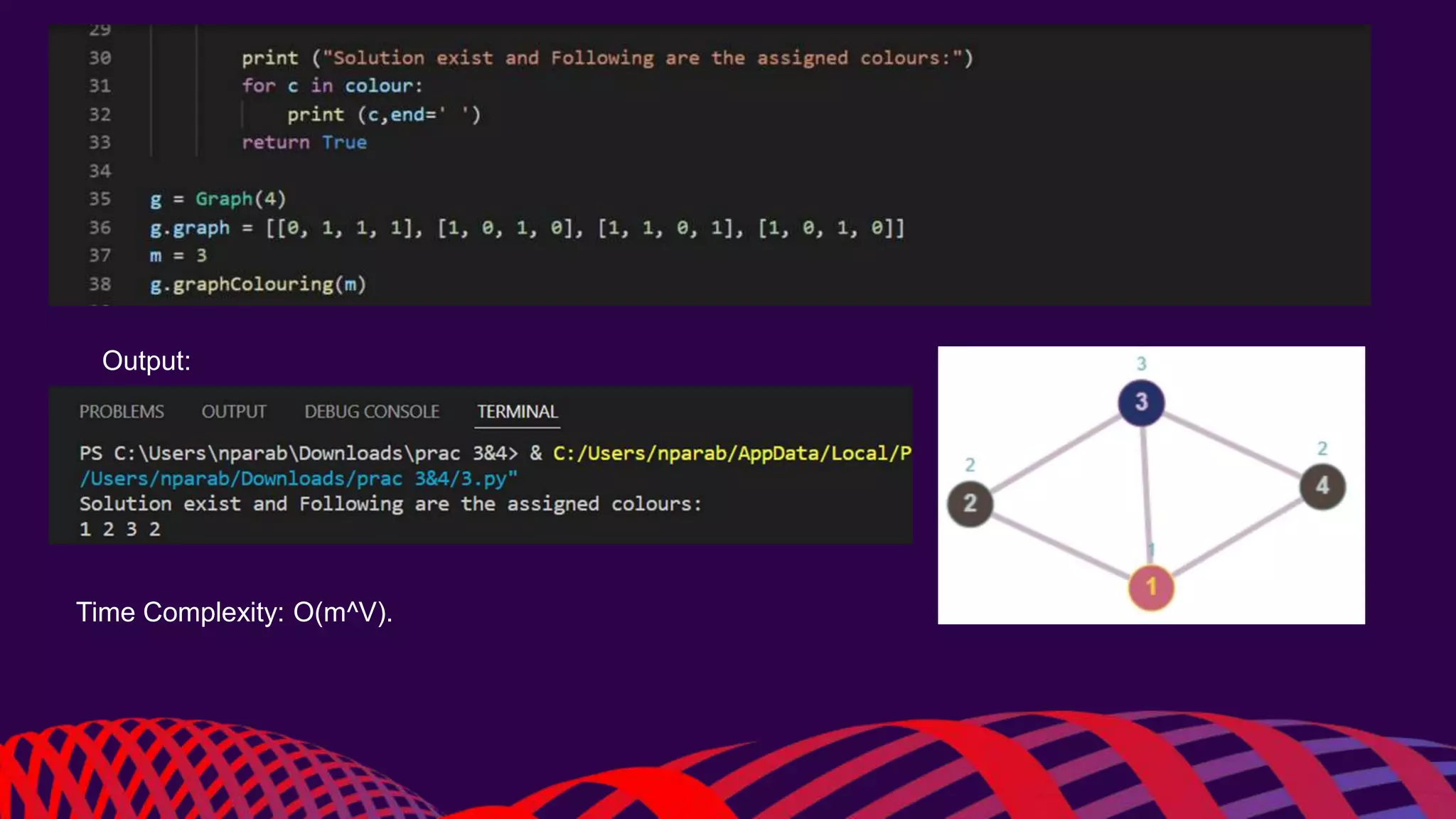
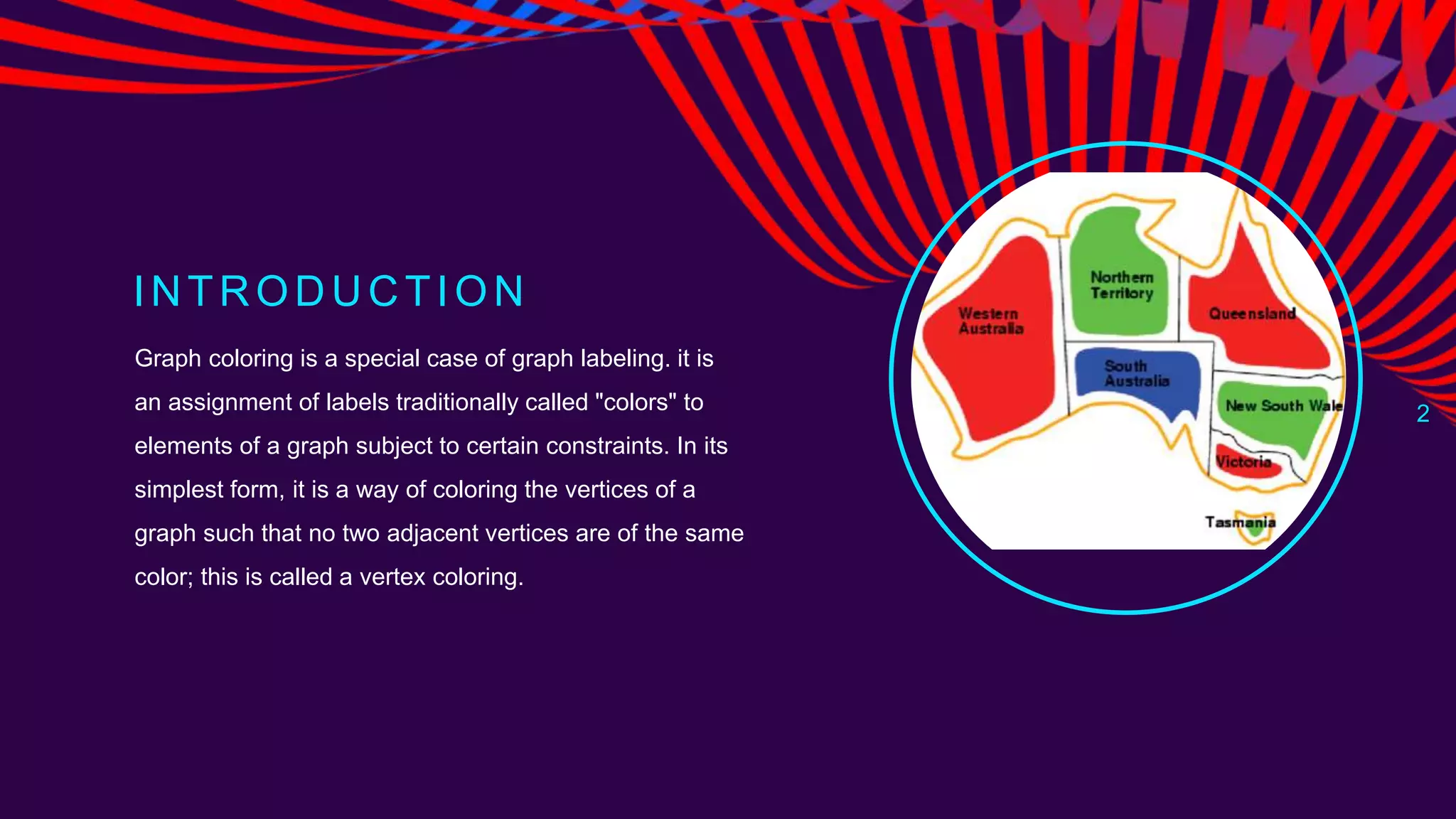
This document discusses the graph coloring problem. Graph coloring involves assigning colors to vertices of a graph such that no adjacent vertices have the same color. The document specifically discusses the M-coloring problem, which involves determining if a graph can be colored with at most M colors. It describes using a backtracking algorithm to solve this problem by recursively trying all possible color assignments and abandoning ("backtracking") invalid partial solutions. The document provides pseudocode for the algorithm and discusses its time complexity and applications of graph coloring problems.

1. GRAPH
COLORING
PROBLEM
• Talha Momin
• Sugam Pandey
• Atharva Parab
• Simran Pardeshi

2. INTRODUCTION
Graph coloring is a special case of graph labeling. it is
an assignment of labels traditionally called "colors" to
elements of a graph subject to certain constraints. In its
simplest form, it is a way of coloring the vertices of a
graph such that no two adjacent vertices are of the same
color; this is called a vertex coloring.
2

3. M-COLORING PROBLEM
• Given an undirected graph and a number m,
determine if the graph can be colored with at most m
colours such that no two adjacent vertices of the
graph are colored with the same color.
• Here coloring of a graph means the assignment of
colors to all vertices.

4. CONCEPT USED:
BACKTRACKING
• Backtracking is a general algorithm for finding solutions to some
computational problems, notably constraint satisfaction problems, that
incrementally builds candidates to the solutions, and abandons a candidate
("backtracks") as soon as it determines that the candidate cannot possibly
be completed to a valid solution.
• Backtracking can be applied only for problems which admit the concept of a
"partial candidate solution" and a relatively quick test of whether it can
possibly be completed to a valid solution.
• Backtracking is an important tool for solving constraint satisfaction
problems, such as crosswords, verbal arithmetic, Sudoku, and many other
puzzles.

5. ALGORITHM
• Create a recursive function that takes the graph, current index,
number of vertices, and output color array.
• If the current index is equal to the number of vertices. Print the
color configuration in output array.
• Assign a color to a vertex (1 to m).
• For every assigned color, check if the configuration is safe, (i.e.
check if the adjacent vertices do not have the same color)
recursively call the function with next index and number of
vertices
• If any recursive function returns true break the loop and return
true.

6. SOLVING THE
PROBLEM
• A 2D array graph[V][V] where V is the number of
vertices in graph and graph[V][V] is an adjacency
matrix representation of the graph. A value
graph[i][j] is 1 if there is a direct edge from i to j,
otherwise graph[i][j] is 0.
• An integer m is the maximum number of colors
that can be used.
• In output the code should show an array which
represents the colors assigned to the vertices.

7. IMPLEMENTATIO
N

9. Output:
Time Complexity: O(m^V).

10. APPLICATIONS :
• Map Coloring: Geographical maps of countries or states where no two adjacent
cities cannot be assigned same color.
• Sudoku: Sudoku is also a variation of Graph coloring problem where every cell
represents a vertex. There is an edge between two vertices if they are in same
row or same column or same block.
• Register Allocation: In compiler optimization, register allocation is the process of
assigning a large number of target program variables onto a small number of CPU
registers. This problem is also a graph coloring problem.
• Mobile Radio Frequency Assignment: When frequencies are assigned to
towers, frequencies assigned to all towers at the same location must be different.
• Bipartite Graphs: We can check if a graph is Bipartite or not by coloring the
graph using two colors. If a given graph is 2-colorable, then it is Bipartite,
otherwise not.

11. CONCLUSION
• Graph coloring enjoys many practical applications as well
as theoretical challenges. Beside the classical types of
problems, different limitations can also be set on the
graph, or on the way a color is assigned, or even on the
color itself. It has even reached popularity with the
general public in the form of the popular number puzzle
Sudoku.
• Graph coloring is still a very active field of research.

12. THANK YOU