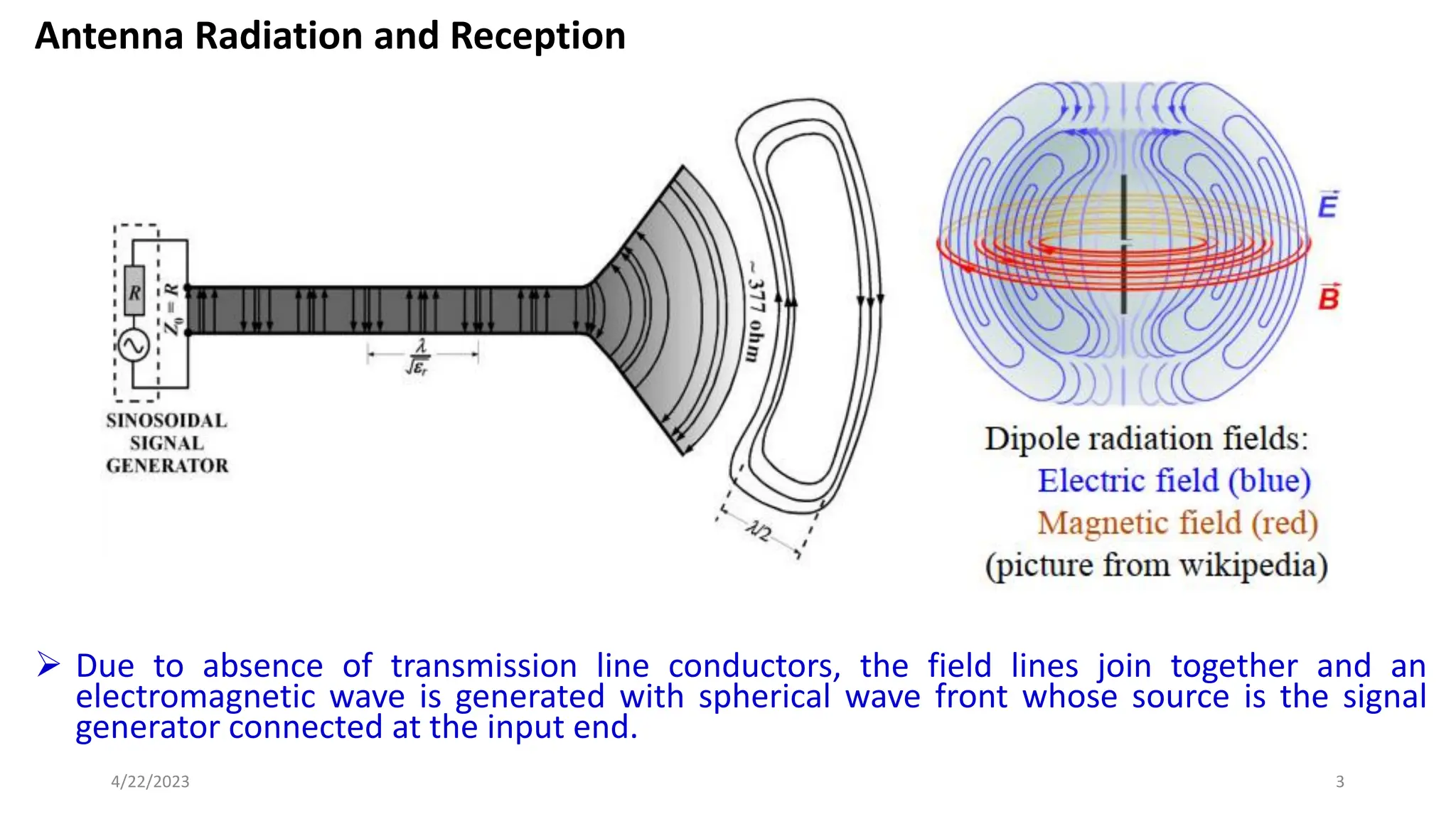
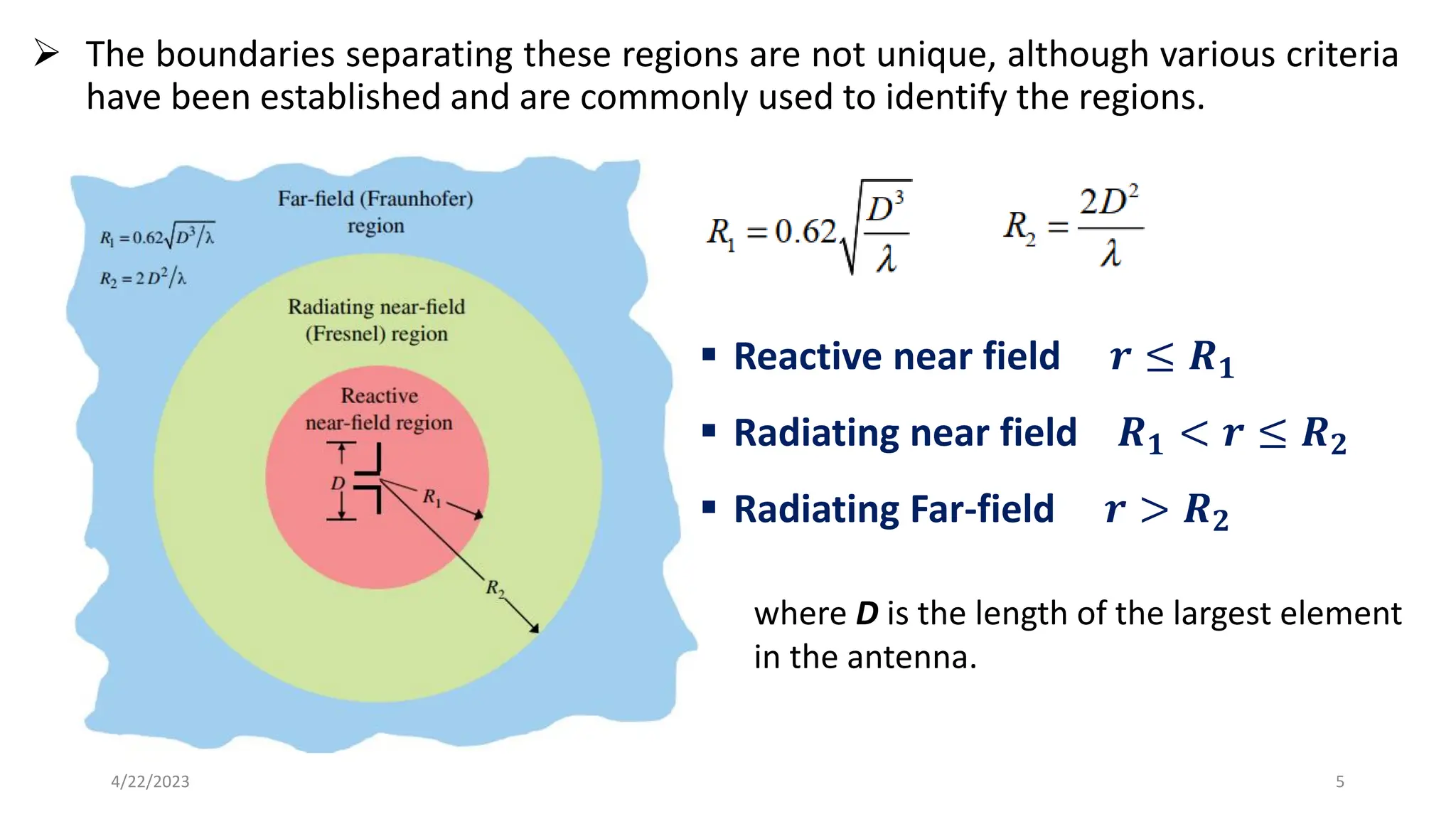
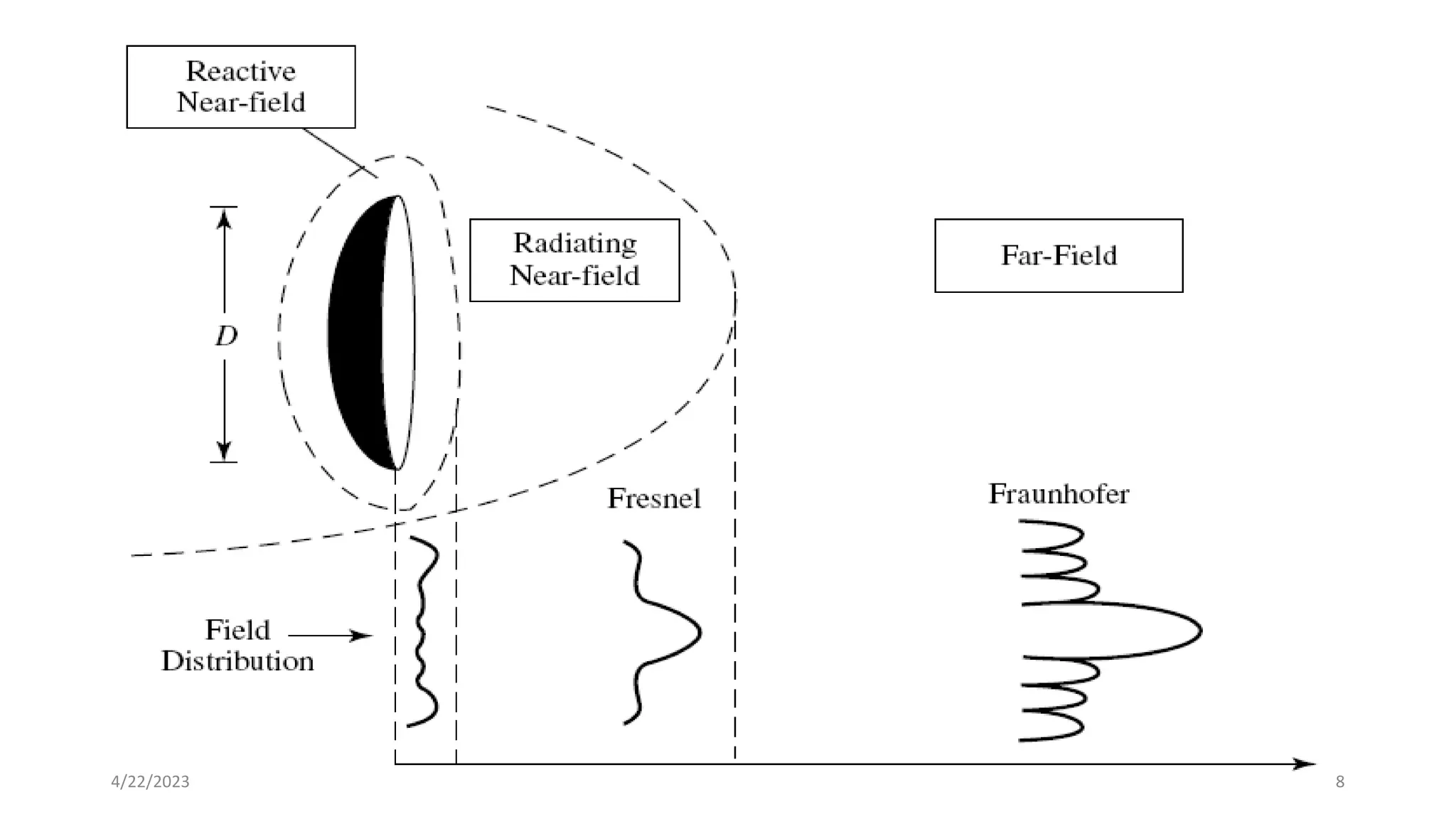
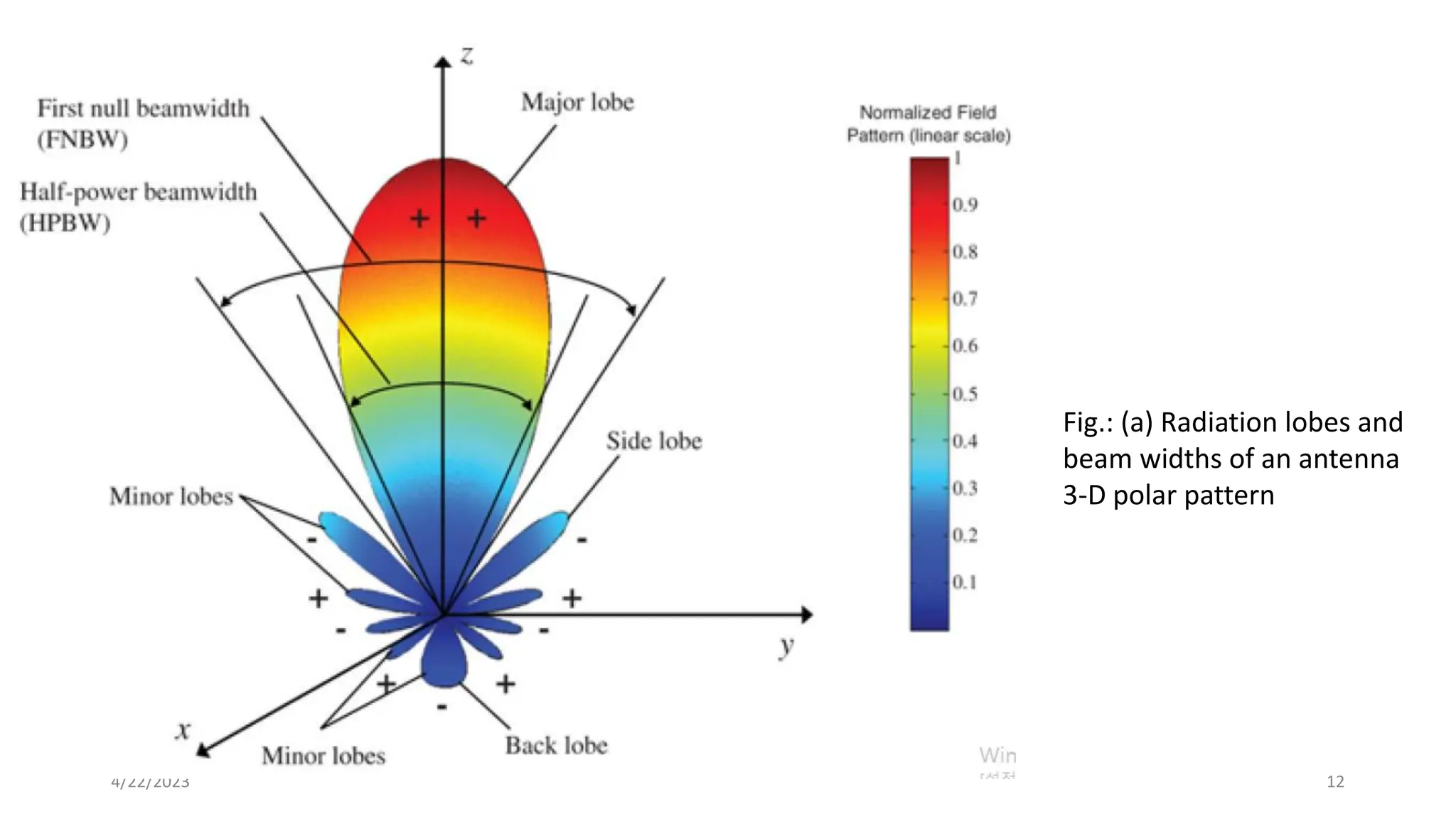
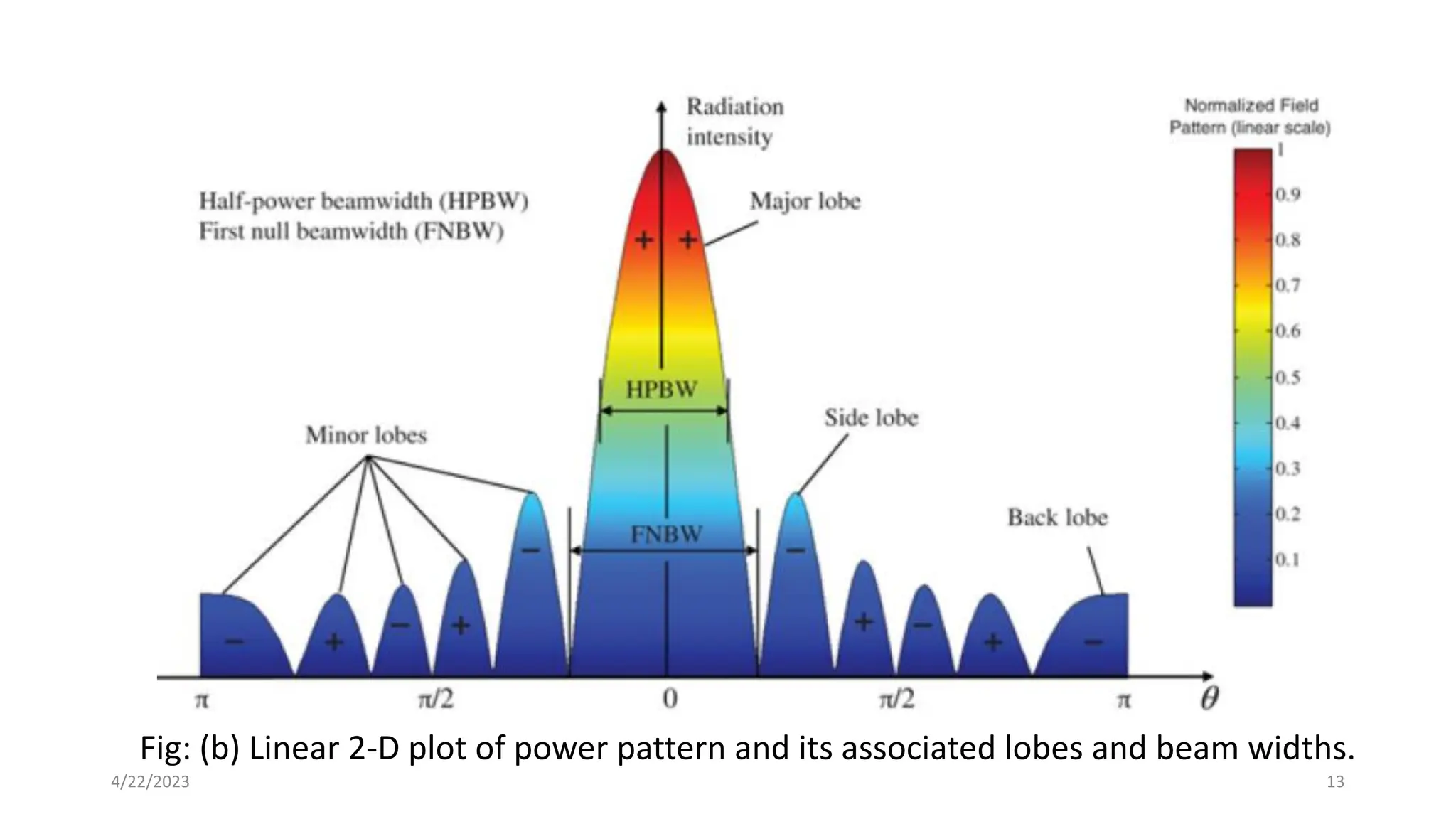
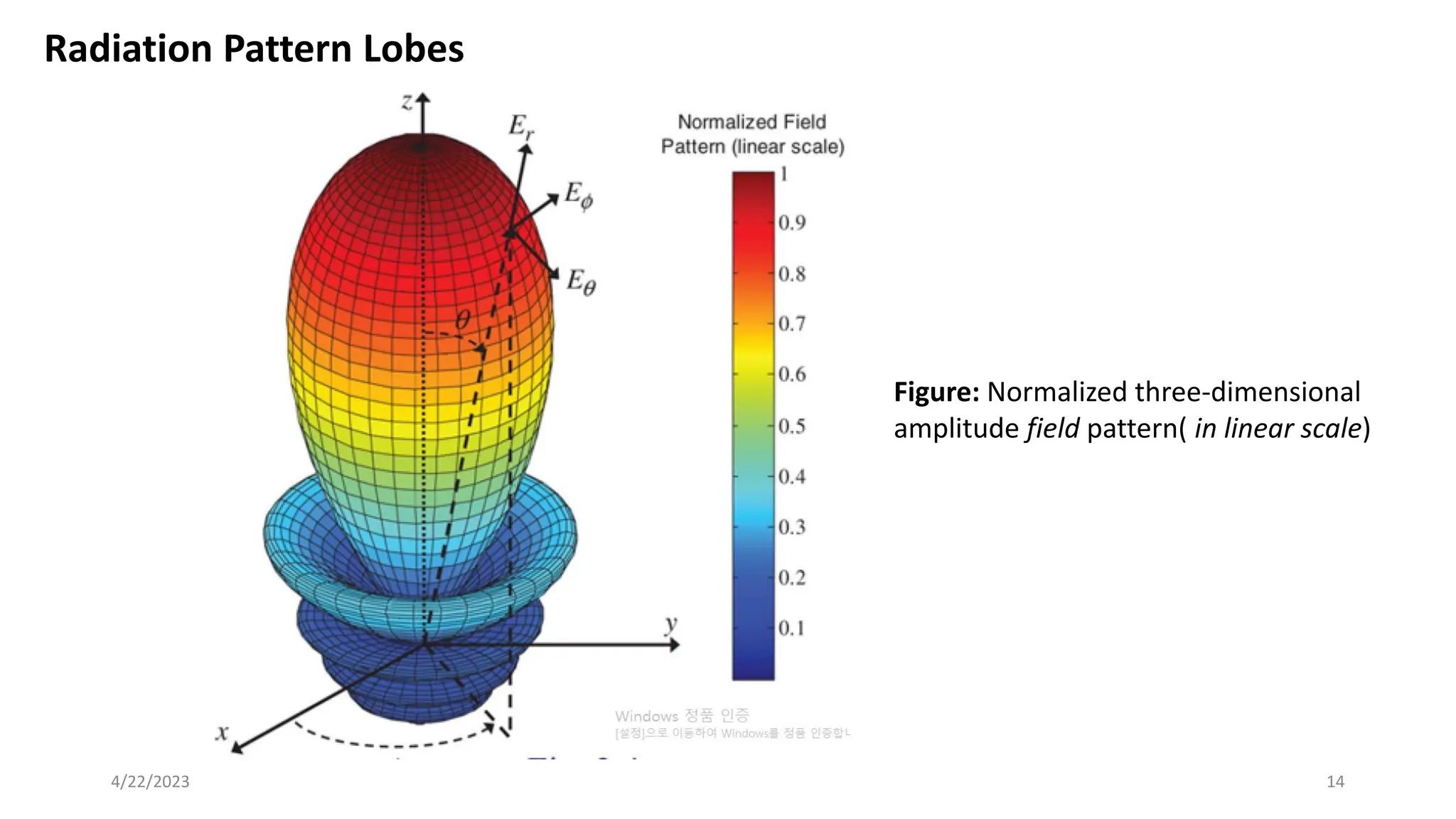
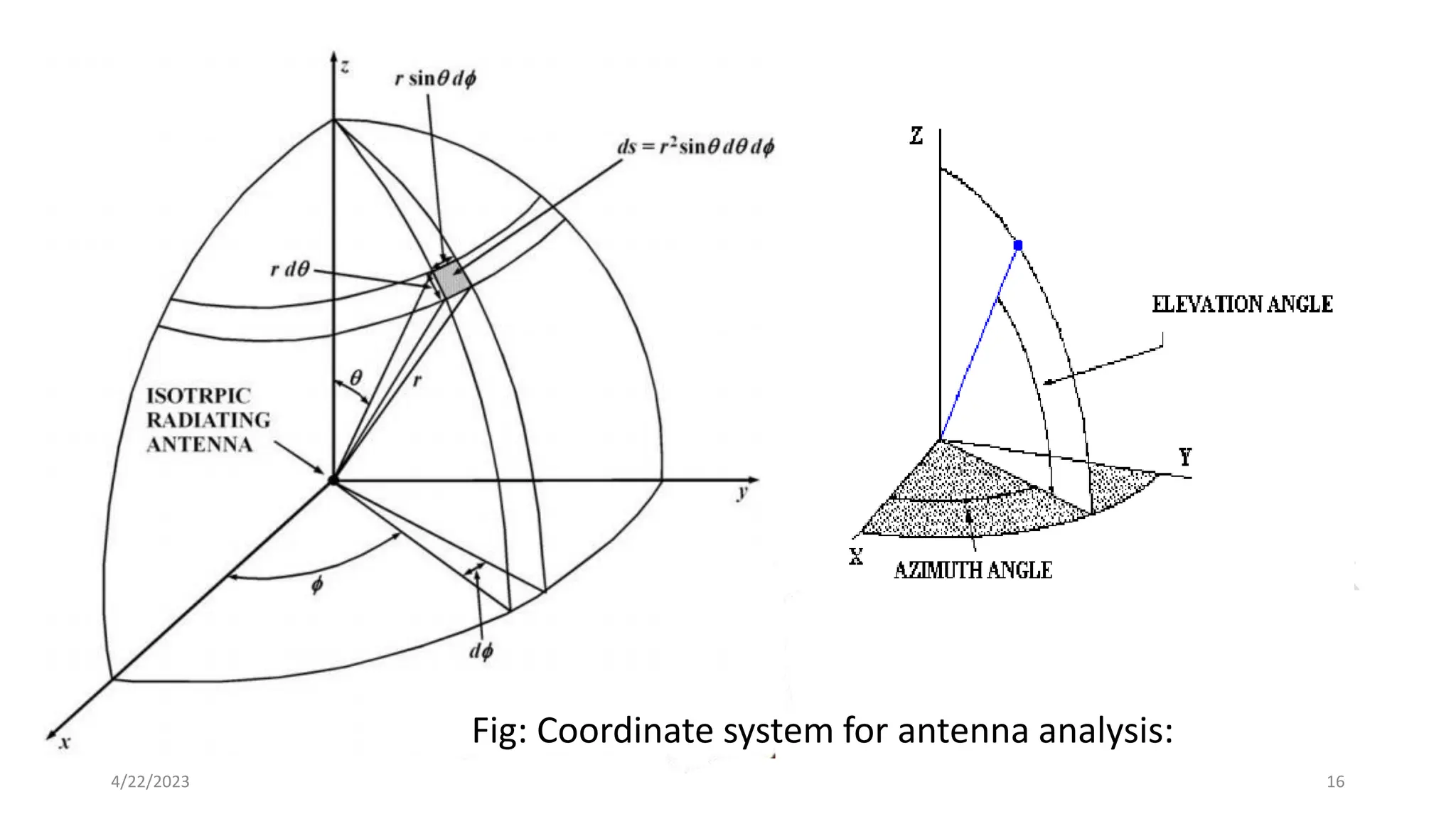
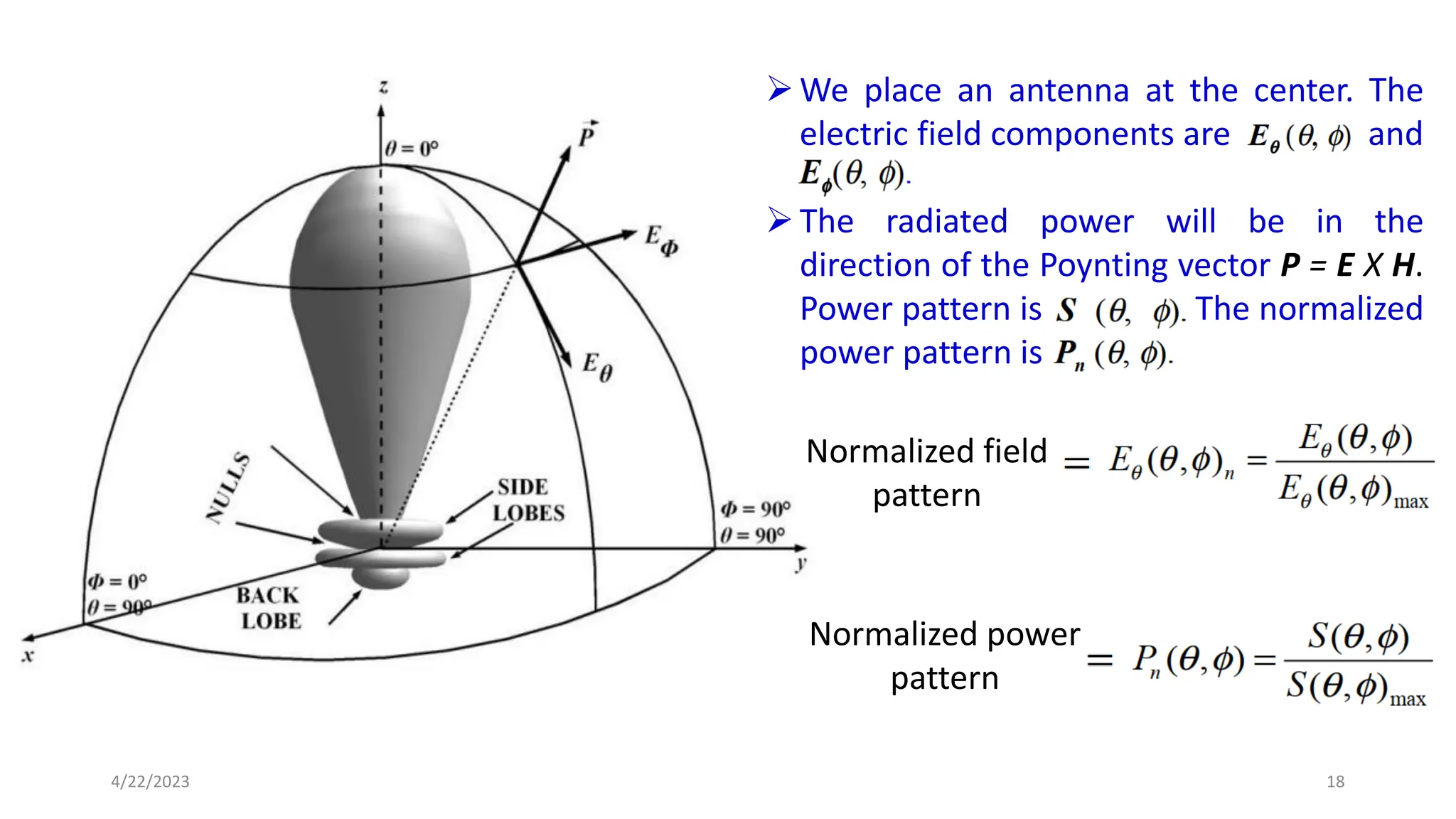
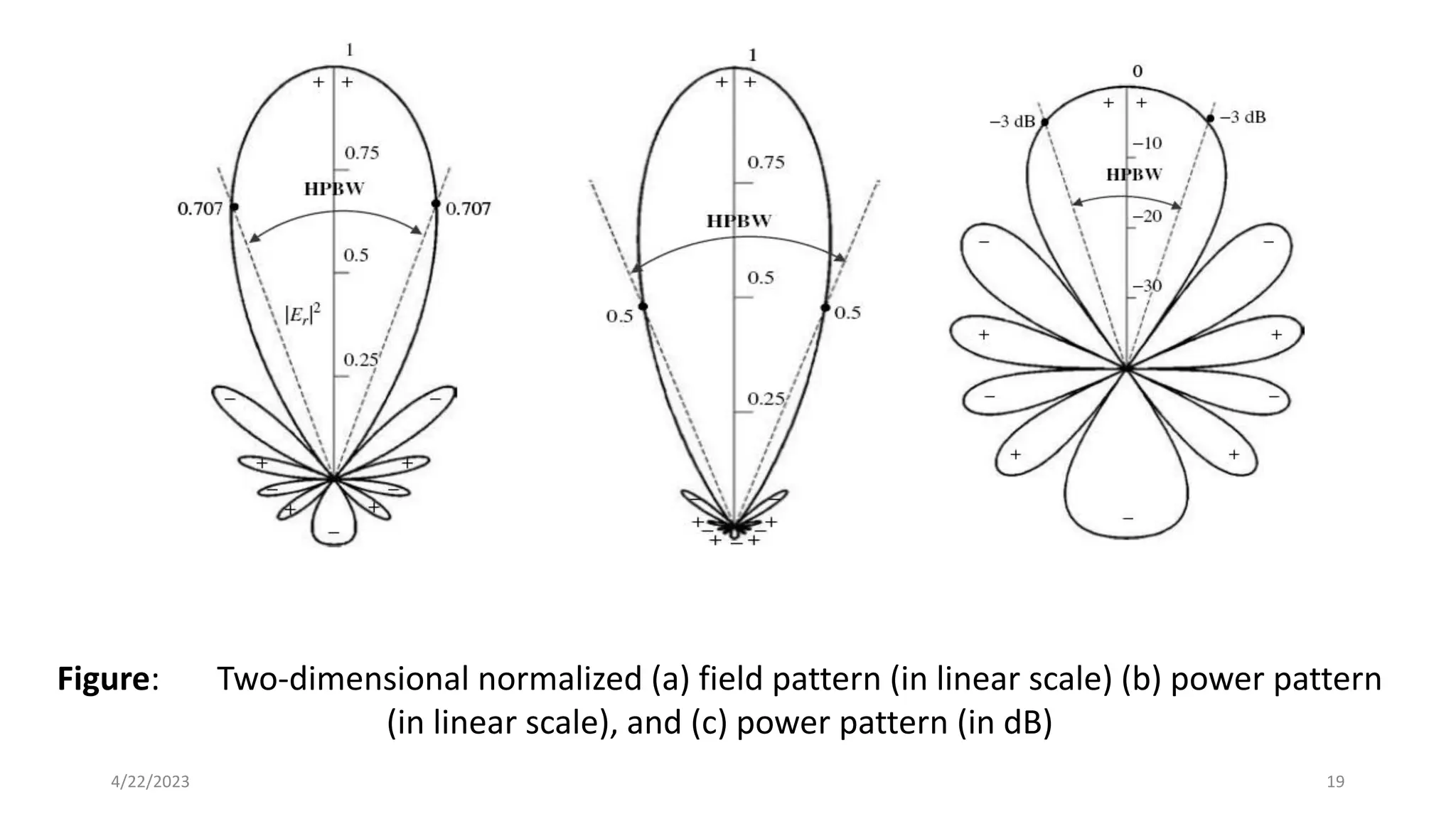
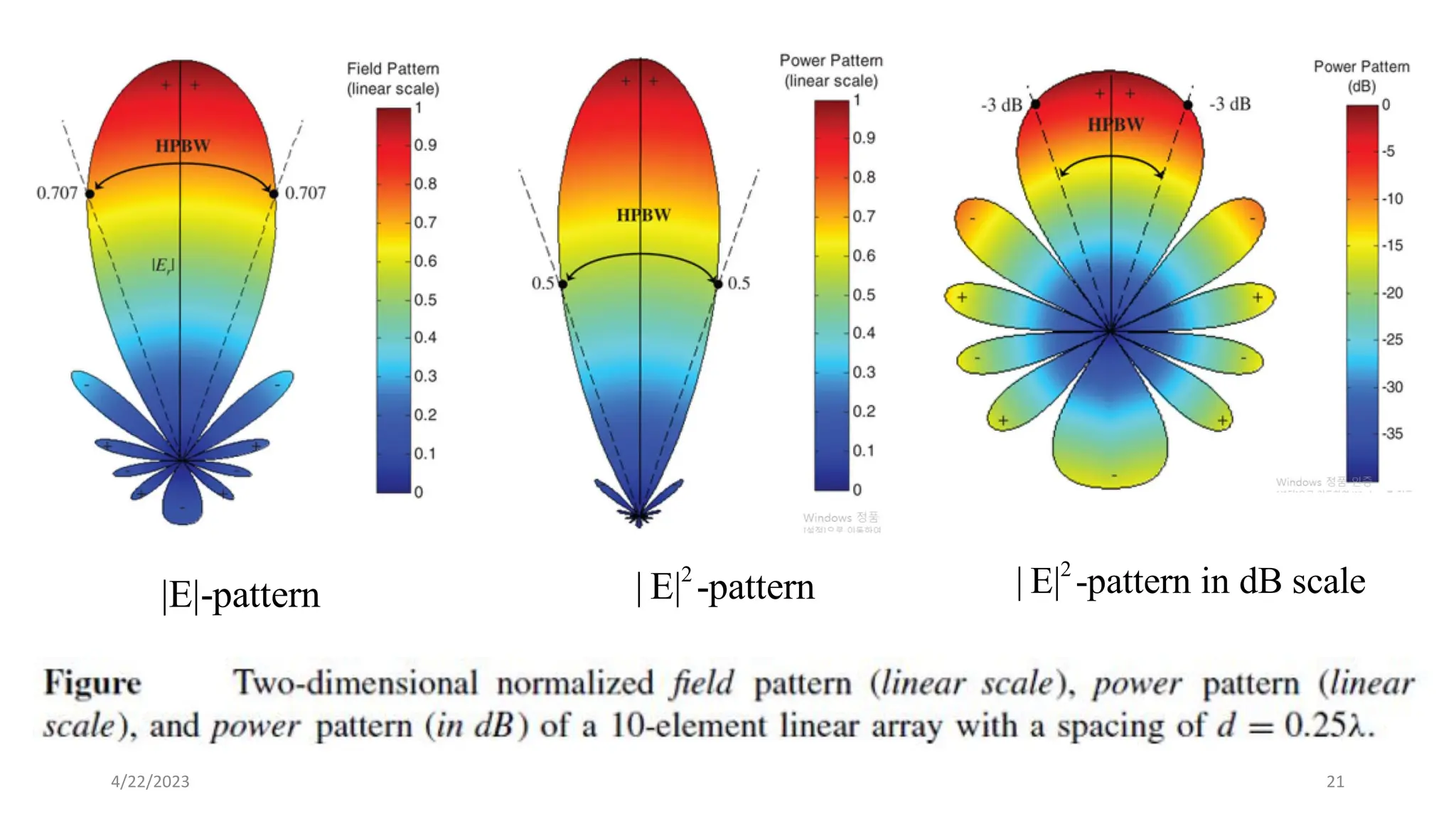
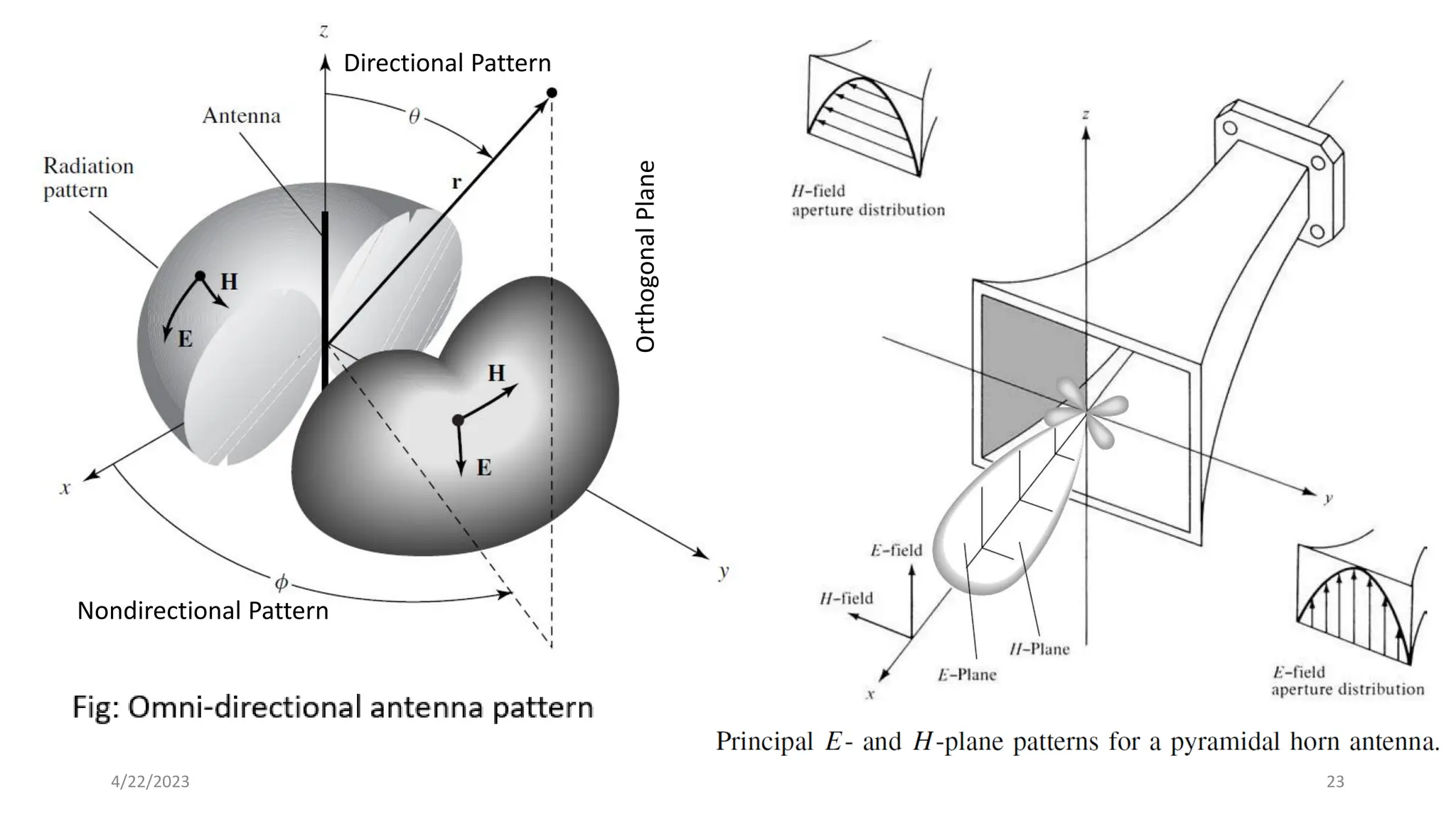
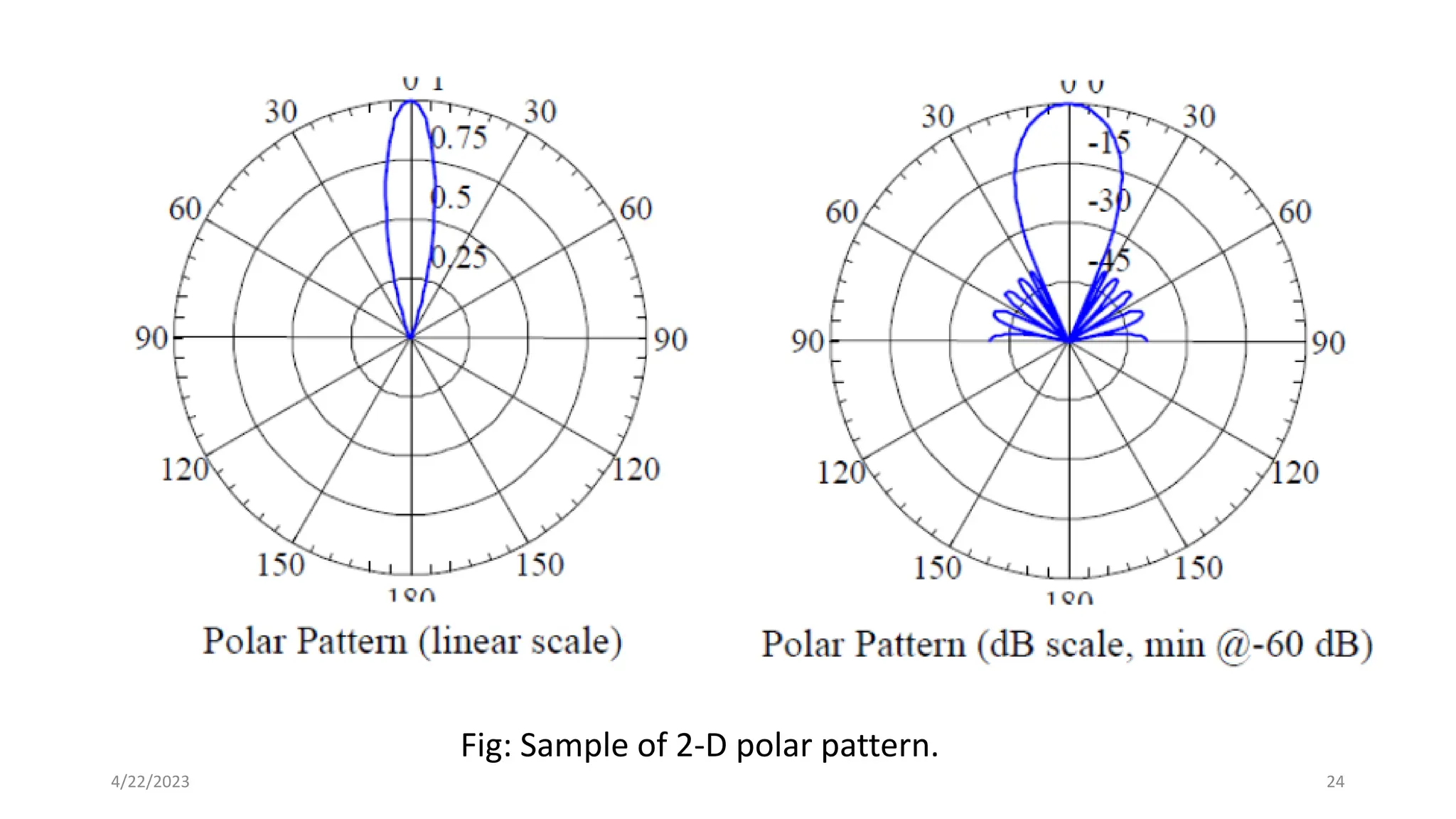
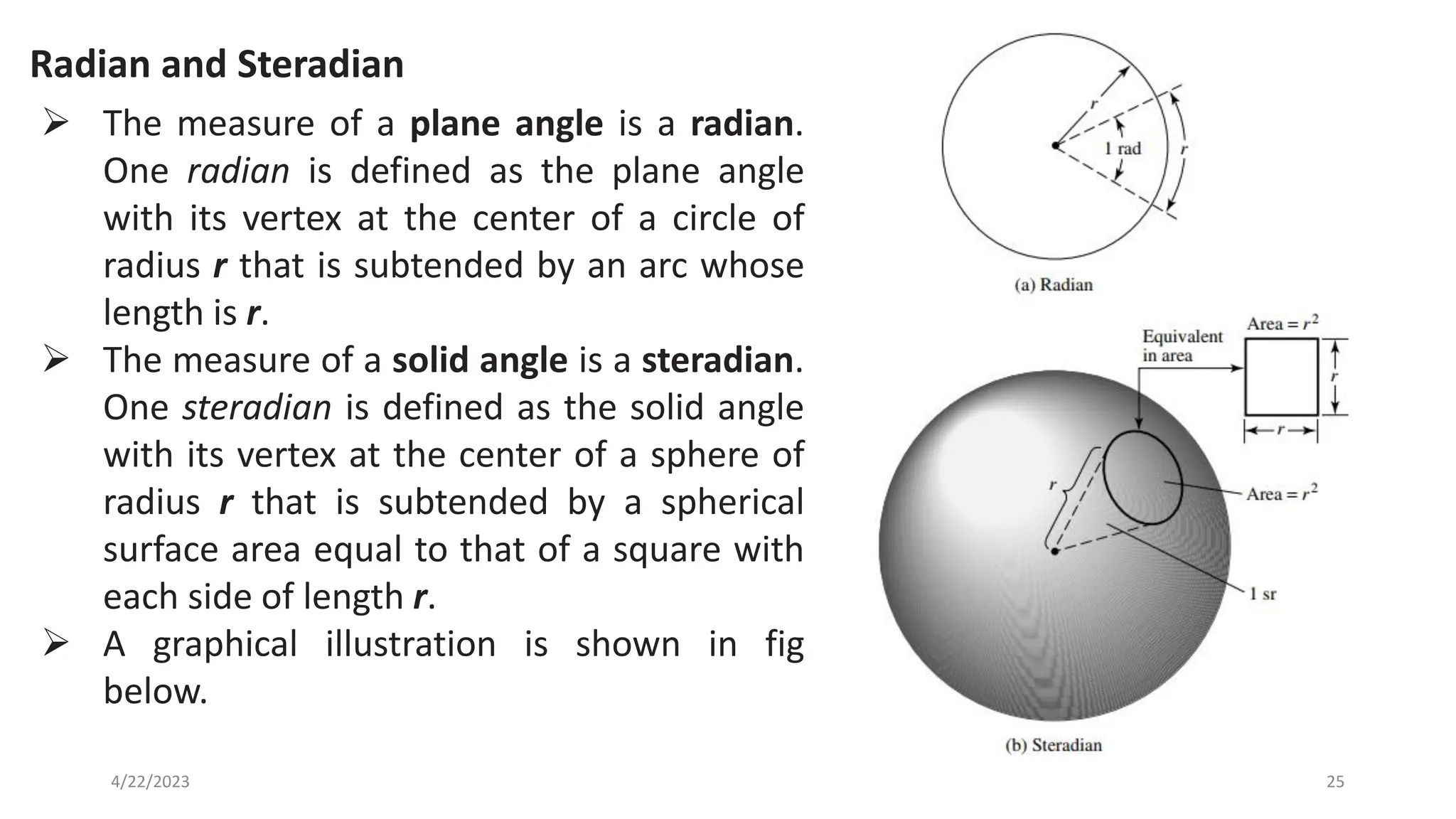
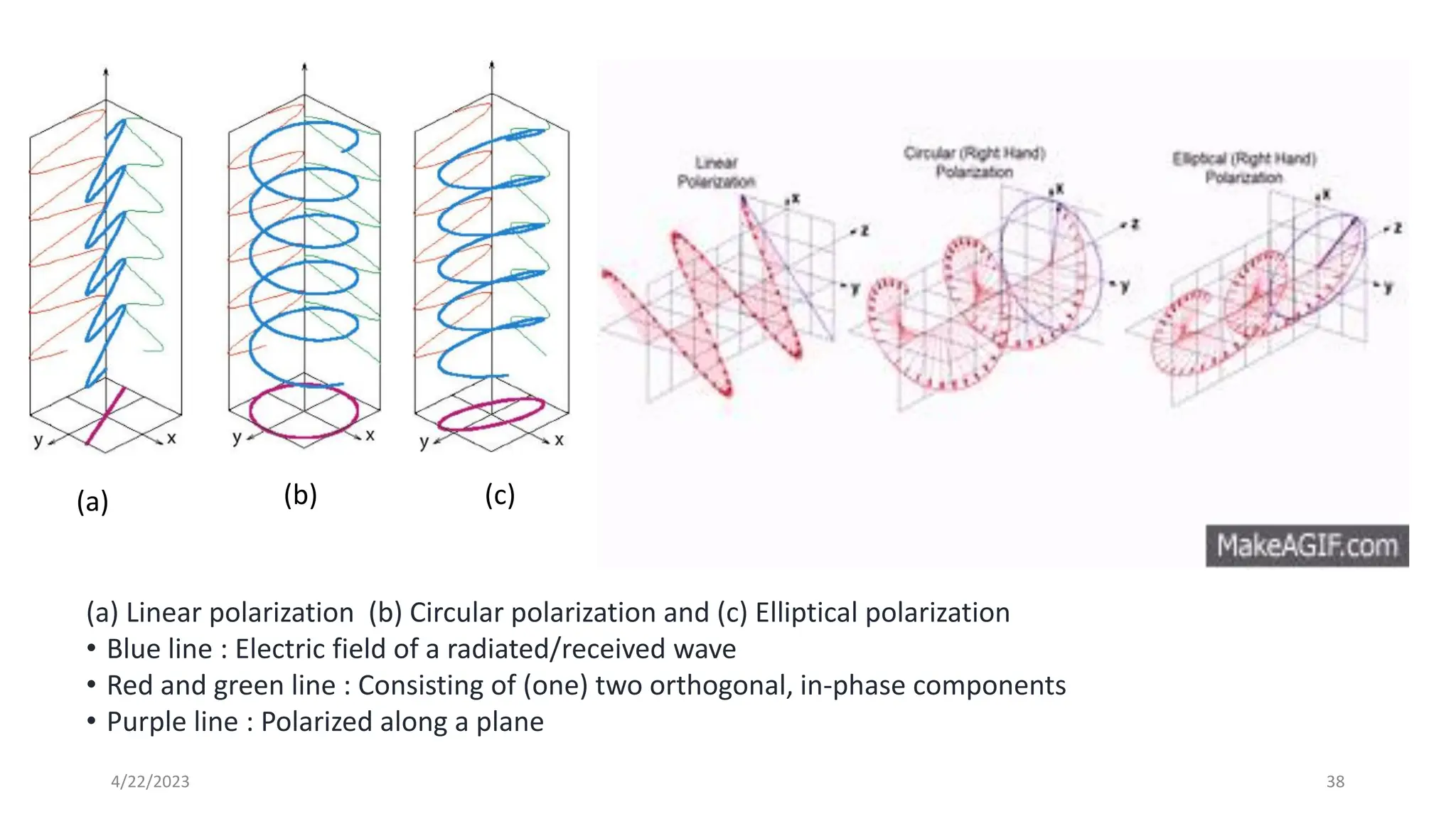
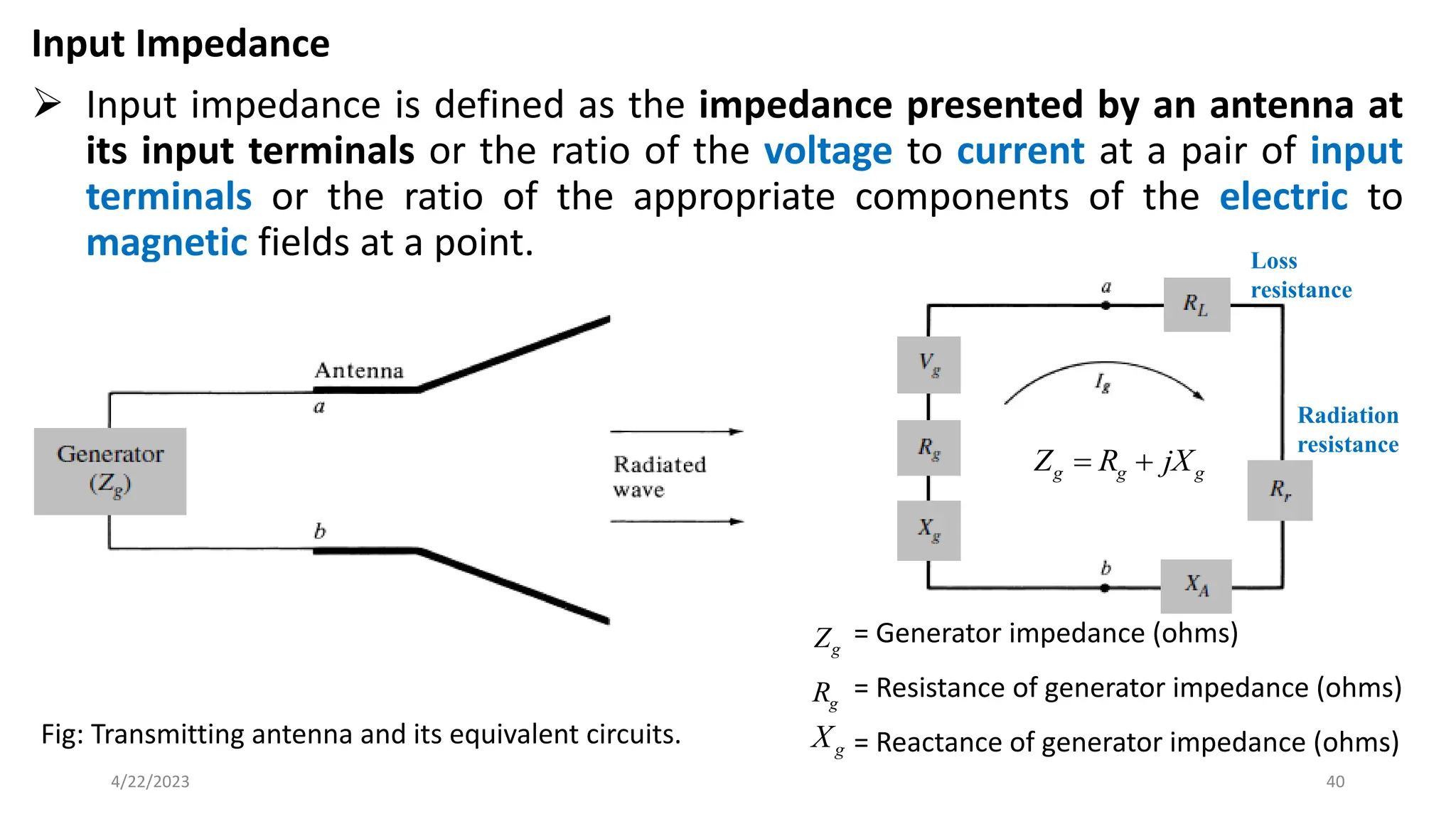
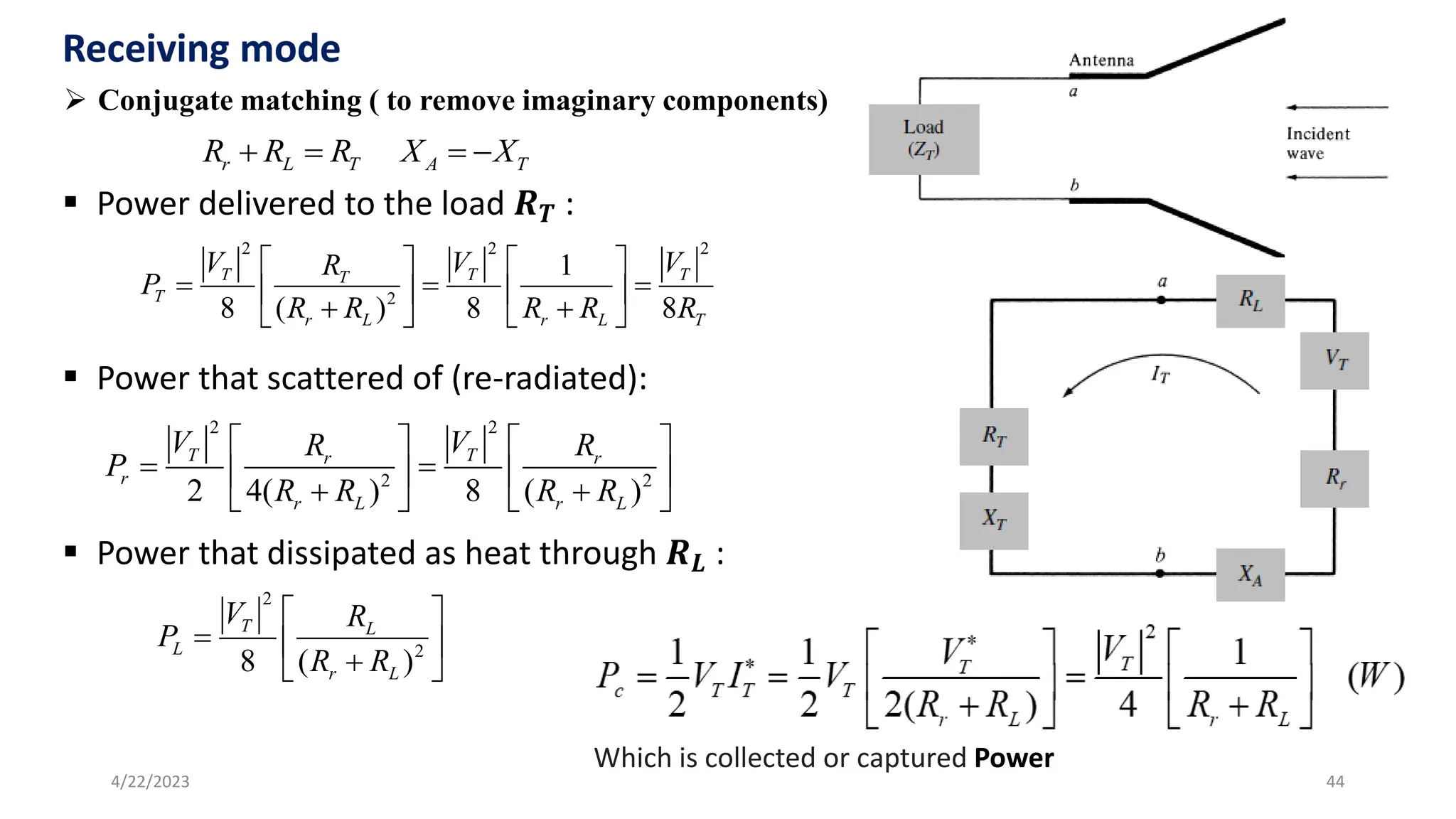
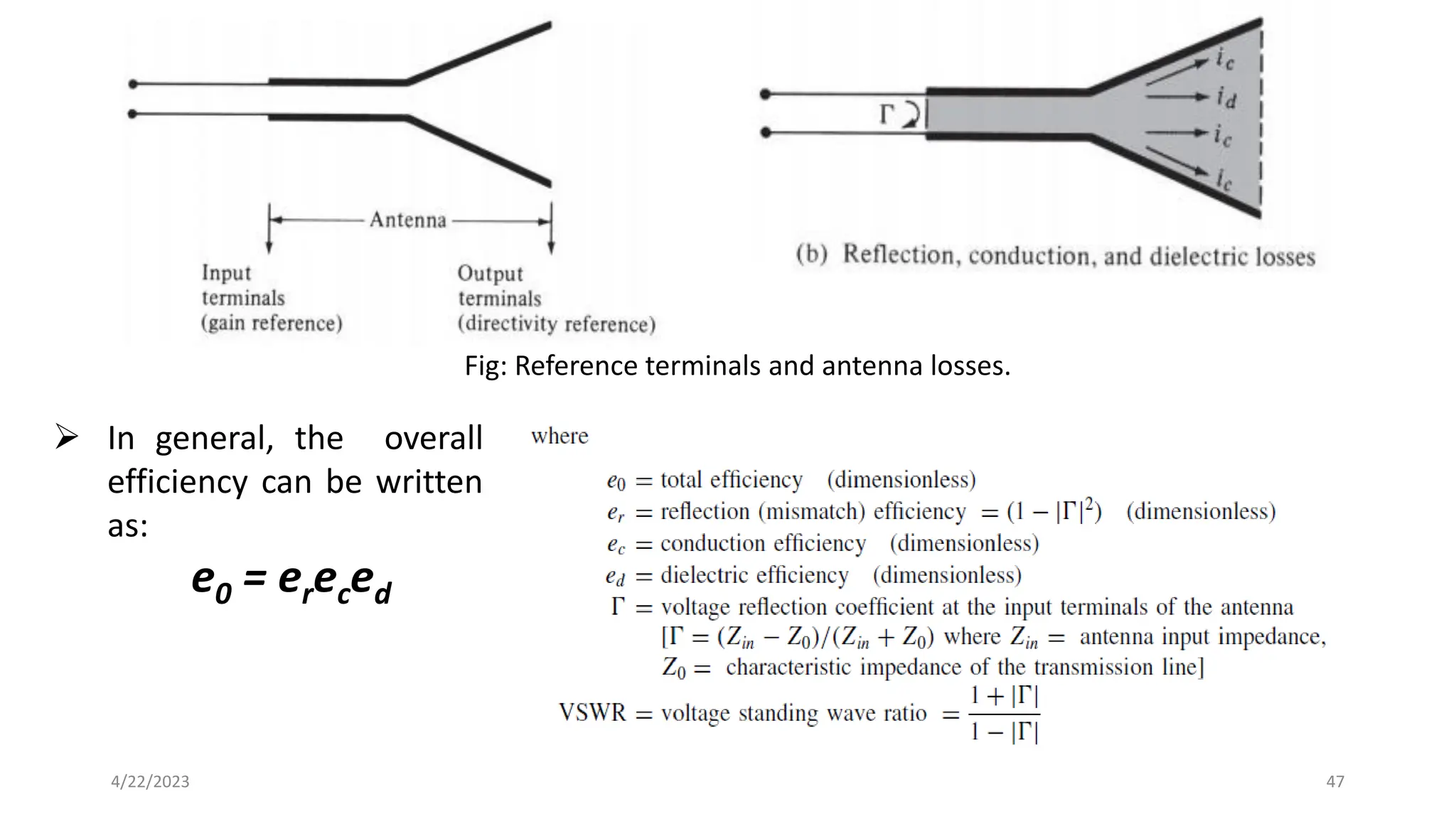
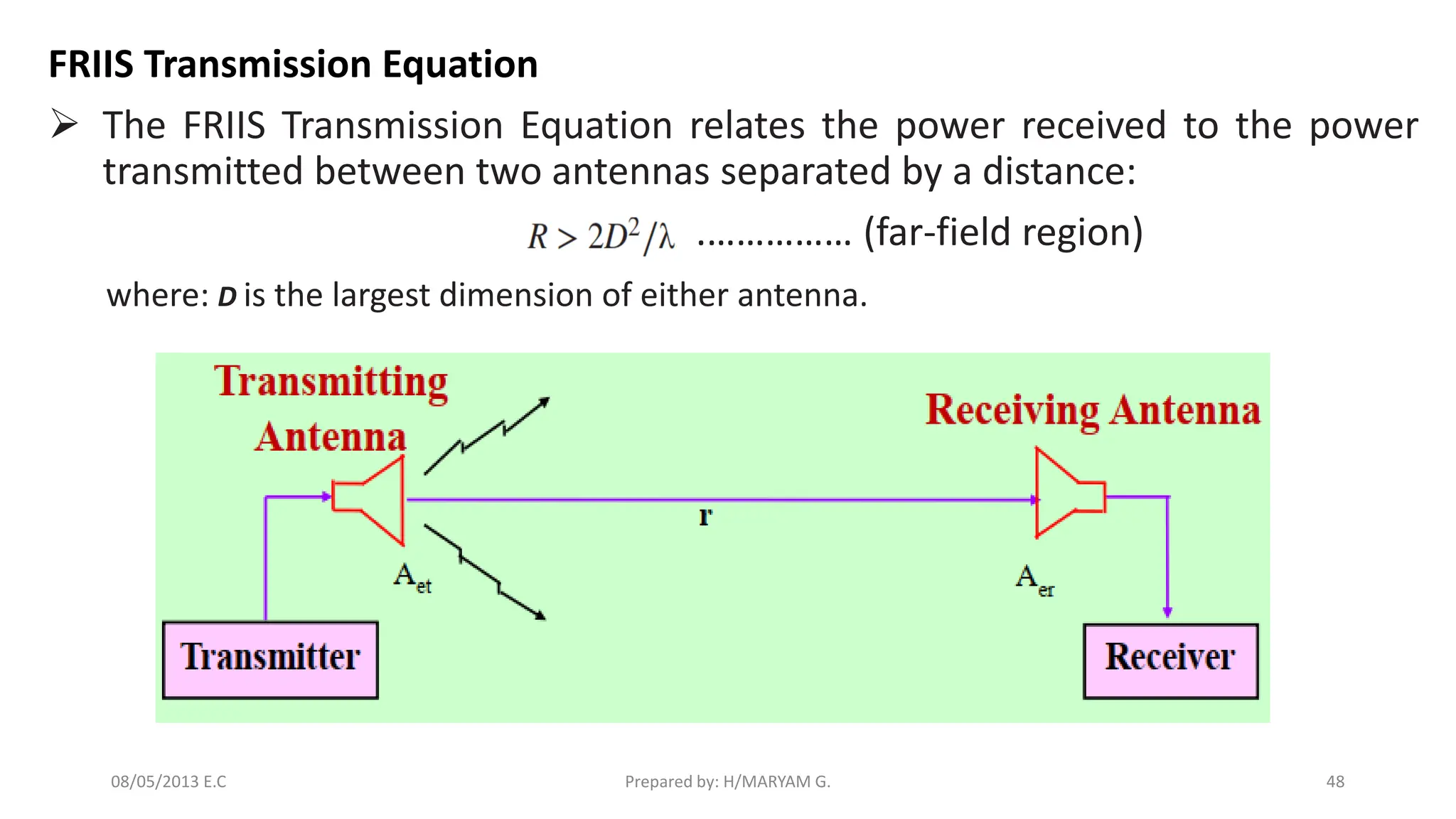
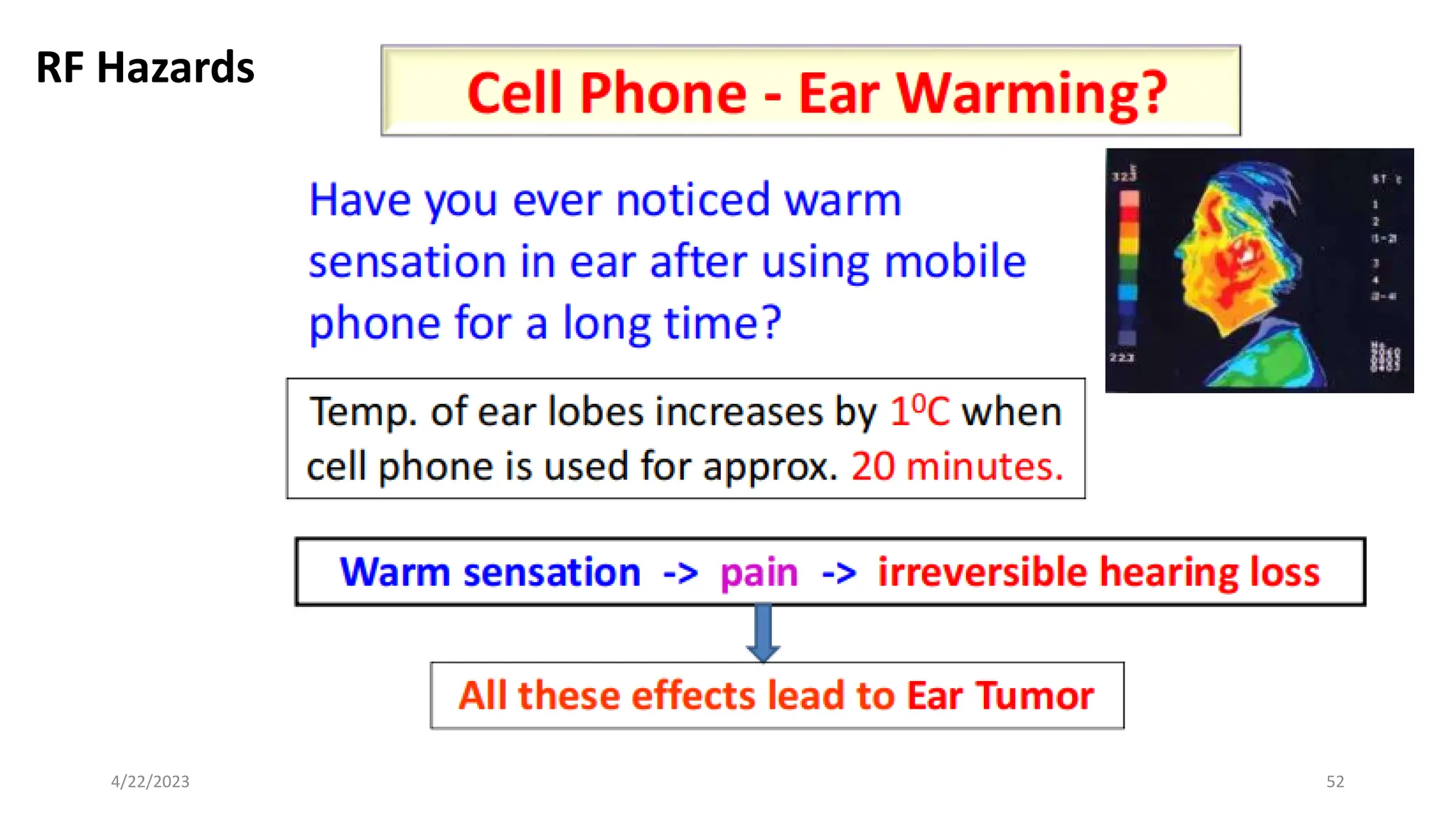
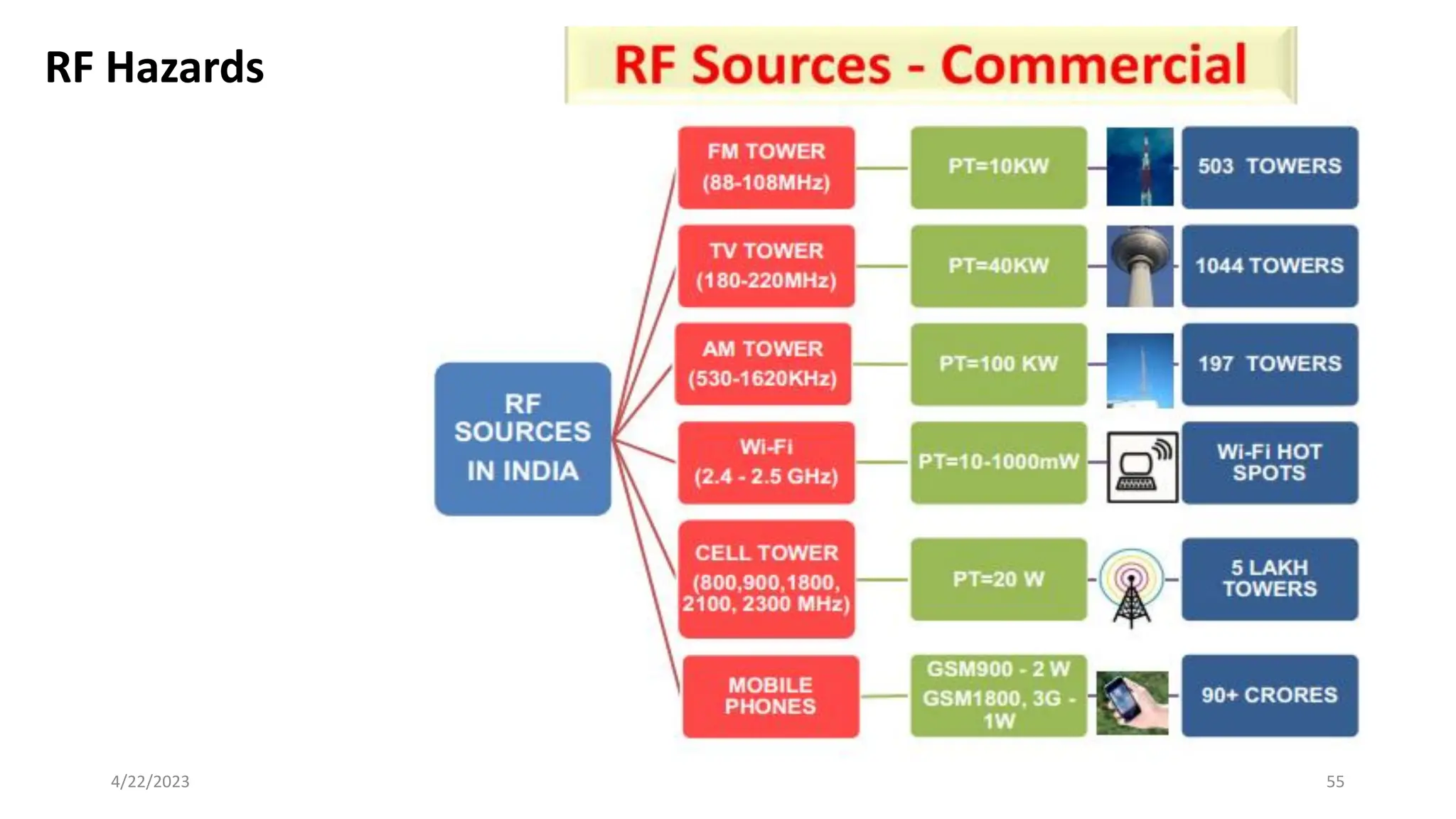
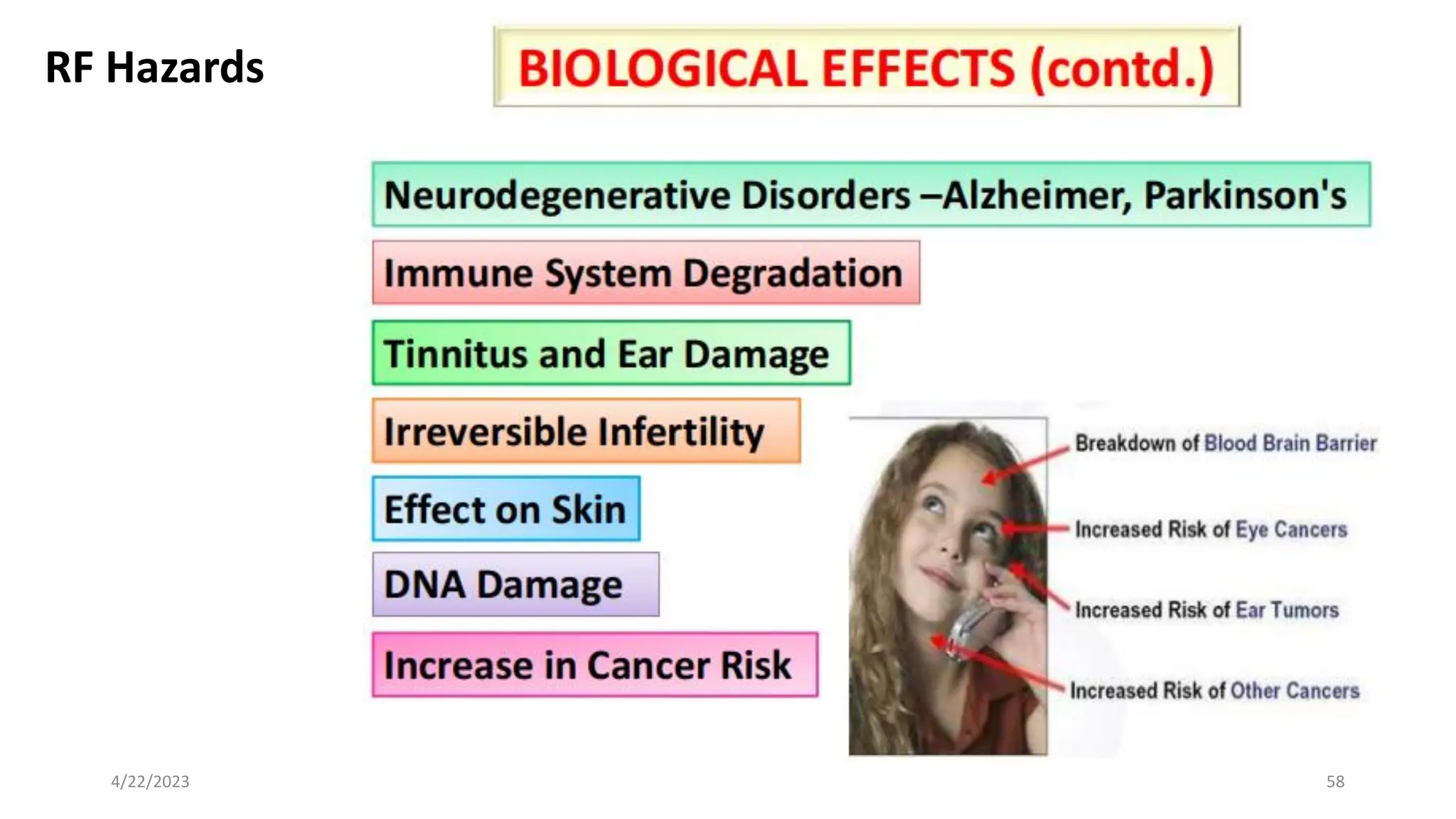
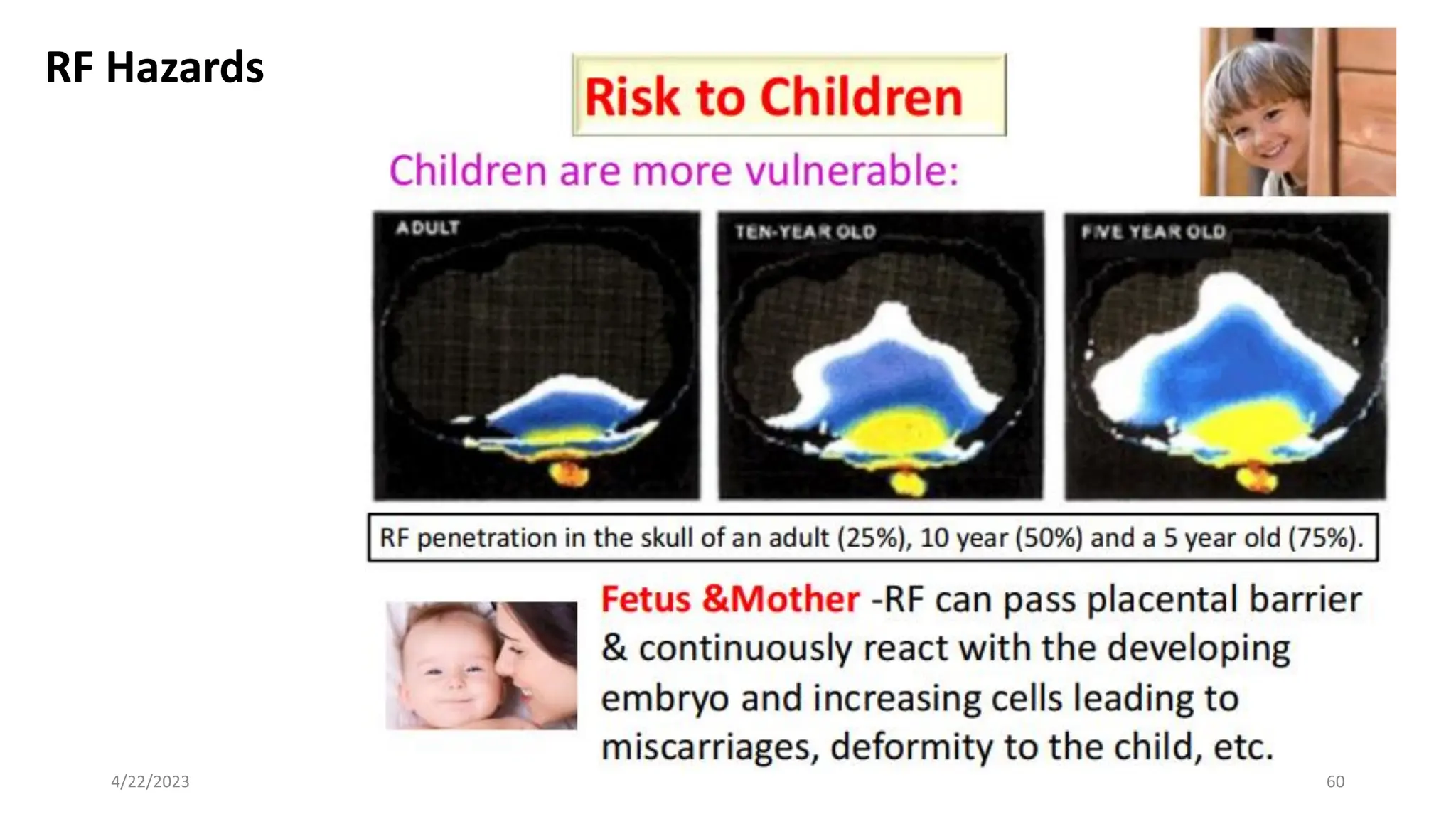
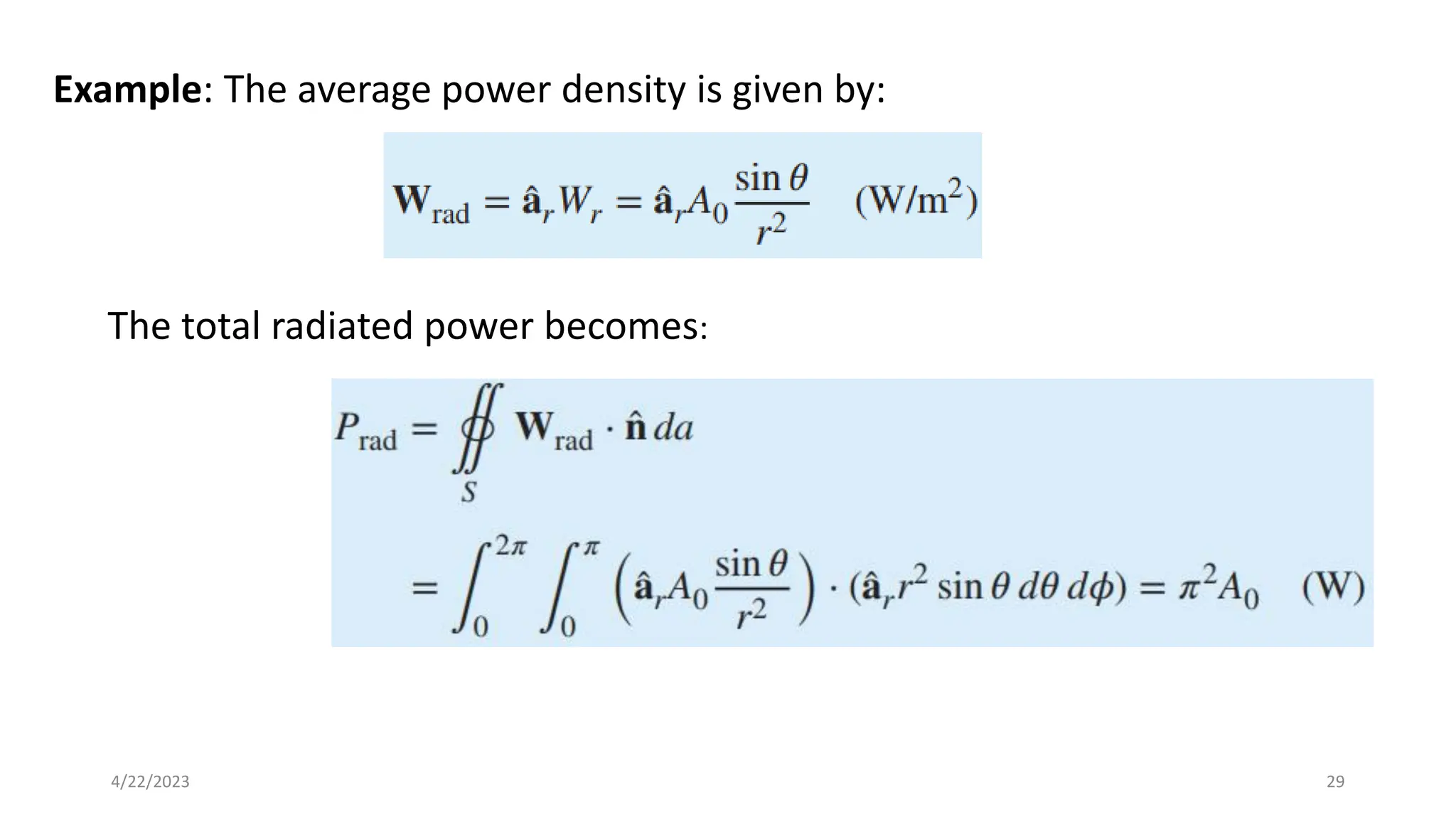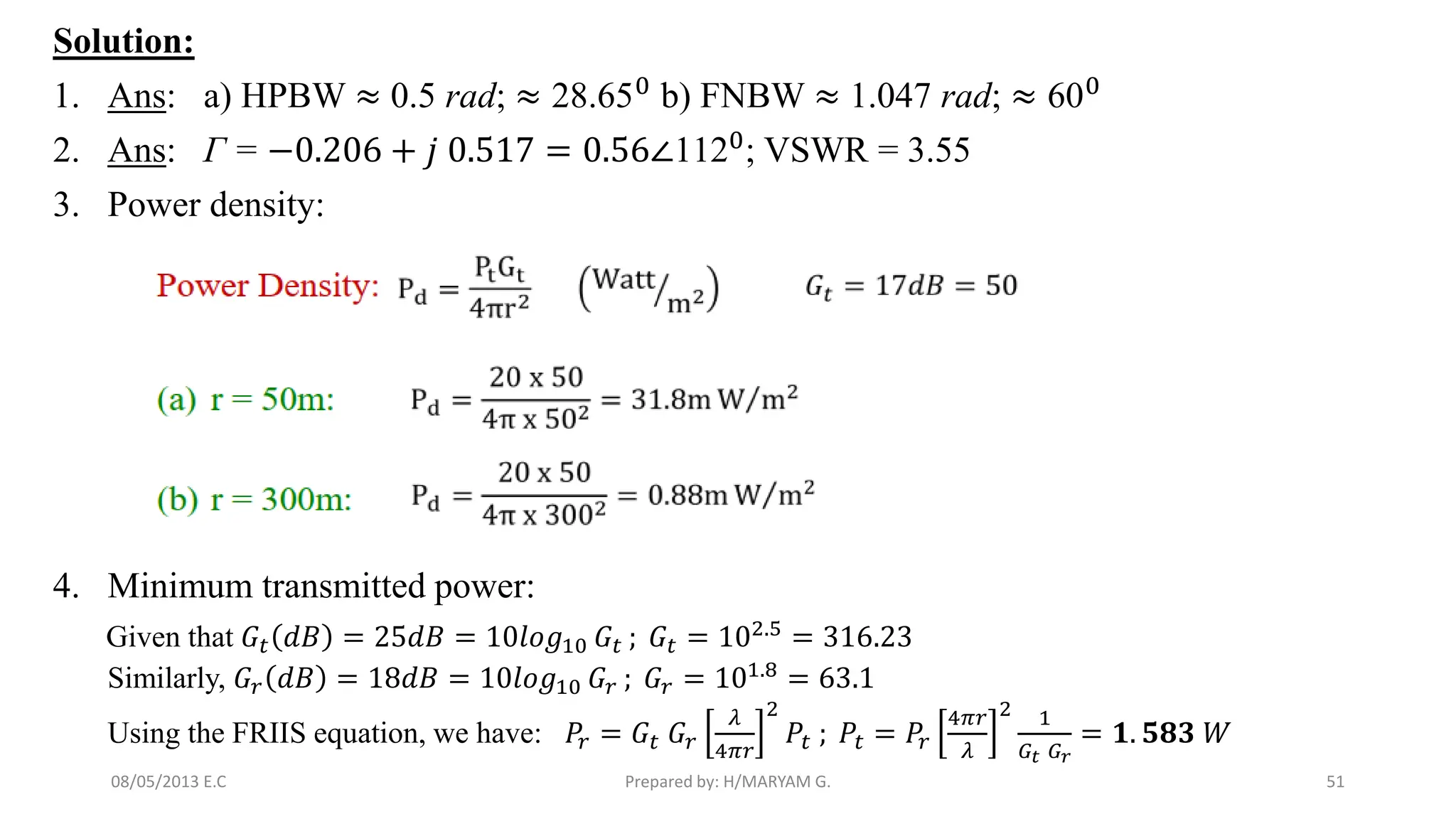The document discusses advanced antenna systems, emphasizing key parameters such as radiation patterns, efficiency, and field regions. It details the classification of antenna regions (reactive near-field, radiating near-field, and far-field) and their impact on radiation characteristics. It also covers antenna metrics like directivity, gain, and bandwidth, vital for understanding antenna performance in communication systems.