This document discusses approximating context-free grammar ambiguity, which is undecidable. It presents a characterization of ambiguity in terms of vertical and horizontal ambiguity. It then introduces an approximation framework based on over-approximations and shows that the regular approximation of context-free grammars (Amn) by Mohri and Nederhof is a decidable approximation that can determine if a grammar is unambiguous.

1. Approximating Context-Free Grammar Ambiguity Claus Brabrand [email_address] BRICS, Department of Computer Science University of Aarhus, Denmark

2. // Abstract “ Approximating Context-Free Grammar Ambiguity” Context-free grammar ambiguity is undecidable. However, just because it’s undecidable, doesn’t mean there aren’t (good) approximations! Indeed, the whole area of static analysis works on “side-stepping undecidability” . We exhibit a characterization of context-free ambiguity which induces a whole framework for approximating the problem. In particular, we give an approximation, A MN , based on the [Mohri-Nederhof, 2000] regular approximation of context-free grammars and show how to boost the precision even further.

3. // Outline Introduction Vertical / Horizontal Ambiguity Characterization of Ambiguity (Over-)Approximation Framework Approximation (A MN ) Assessment Related Work Conclusion

4. // Context-Free Grammar N finite set of nonterminals  finite set of terminals s  N start nonterminal  : N  P (E*) production function , E = N   G =  N,  , s,   Assume : All n  N reachable (from s) All n  N derive some (finite) string L : G  P (  *) language of G, L (G)

5. // Relevant CFG Decision Problems Decidable : Membership:   L (G CFG ) Emptyness: L (G CFG ) =  Intersection (w/ REG): L (G CFG )  L (R REG ) = L (C CFG ) … constructively Undecidable : Intersection (w/ CFG): L (G CFG )  L (G’ CFG ) ? … Ambiguity :  *: 2 derivation trees ?

6. // Ambiguity: Undecidable! Algorithms: Undecidable ! However…  T s  T’ s  = unambiguous ambiguous Ambiguity :  *: 2 derivation trees ? ?

7. // “Side-Stepping Undecidability” Unsafe approximation : Safe approximation : However, just because it’s undecidable, doesn’t mean there aren’t (good) approximations ! Indeed, the whole area of static analysis works on “ side-stepping undecidability ” . unambiguous ambiguous safe (over-) approximation unambiguous ambiguous safe (under-) approximation unambiguous ambiguous unsafe approximation

8. // Motivation Use safe (over-) approximation : “ Yes! ”  “G guaranteed unambiguous”!!! Safely use any GLR parser on G Because: never two parses at runtime! Hence: dynamic parse ambiguity  static parse ambiguity unambiguous ambiguous Yes! .

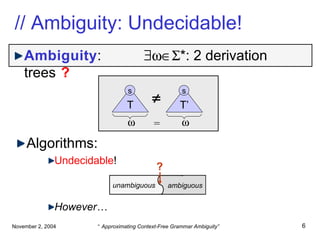
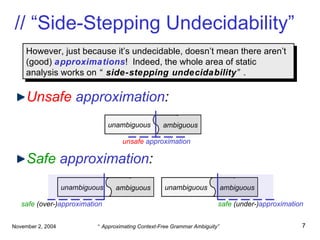
9. // Motivation (cont’d) Undecidability means: “there’ll always be a slack ”: However, still useful! Possible interpretations of “ No? ”: Treat as error (reject grammar): “ Please redesign your grammar” (as in [LA]LR(k)) Treat as warning : “ Here are some potential problems” unambiguous ambiguous No? . .

10. // Vertical Ambiguity “ Vertical ambiguity” : Example:  n  N :  ,  ’   (n) :    ’  L (  )  L (  ’) =  x a y Z : x A y : x B y A : a B : a Ambiguous string: ~ “ reduce/reduce conflict ” in [Yacc]  G

11. // Horizontal Ambiguity “ Horizontal ambiguity” : where: Example:  n  N :    (n):  i  [1..|  |-1]: L (  0 ..  i-1 ) L (  i ..  |  |-1 ) =  : P (  *)  P (  *)  P (  *) X Y = { x a y | x,y  *  a  +  x,x a  L (X)  y, a y  L (Y) } x a y Z : A B A : x a : x B : a y : y Ambiguous string: ~ “ shift/reduce conflict ” in [Yacc]  G      

12. // Characterization of Ambiguity Theorem 1: Lemma 1a: (“  ”) Lemma 1b: (“  ”) G  G  G unambiguous G  G  G unambiguous G  G  G unambiguous

13. // Proof (Lemma 1a): “  ” … or contrapositively: Proof: Assume G ambiguous (i.e.  2 der. trees for  ) Show: by induction in max height of the 2 derivation trees G  G  G unambiguous G ambiguous  G  G G  G

14. // Proof (Lemma 1a): “  ” (Base) Base case (height  1): The ambiguity means that (for p  p’) : Which means: i.e., we have a vertical ambiguity: N  ’ 1  N  1   L (  )  L (  ’)  {  }   p p’ = G

15. // Proof (Lemma 1a): “  ” (I.H.) Induction step (height  n): Assume induction hypothesis (for height  n-1) The ambiguity means: N n-1  N  n-1  i  ’ i’ … …  i … …  ’ i’ p p’ 1 1  |  -1| =  ’ 0  ’ |  ’-1|  0 .. .. .. ..  = 

16. // Proof (Lemma 1a): “  ” (p  p’) Case p = q (different production): … but then  i.e., we have a vertical ambiguity: L (  )  L (  ’)  {  }   p  p’ G N n-1  N  n-1  i  ’ i’ … …  i … …  ’ i’ p p’ 1 1  |  -1| =  ’ 0  ’ |  ’-1|  0 .. .. .. ..  = 

17. // Proof (Lemma 1a): “  ” (p=p’,1) Case p  q (same prod.  ): i.e. “the top of the trees are the same” Case :  ambiguity in subtree i ( deriving same  i ): Induction hypothesis (this subtree)   i :  i =  ’ i p = p’  i :  i =  ’ i  N n-1  N  n-1  i  i … …  i … …  i’ p p’ 1 1  |  -1| =  0  |  -1|  0 .. .. .. ..  =  G G

18. // Proof (Lemma 1a): “  ” (p=p’,2) Case p  q (same prod.  ): Case : … but then: (assume WLOG ): Now pick any k : ...then: N n-1  N  n-1  i . … .  i p  i :  i   ’ i p = p’ p 1 1  i :  i =  ’ i   i :  i =  ’ i   j  i:  j   ’ j =   j  j  ’ i . … .  i  j  ’ j i  k < j L (  0 ..  k ) L (  k+1 ..  |  | )    k k least such i 2 nd least such j G  

19. // Proof (Lemma 1b): “  ” Contrapositively: Assume “ ” (vertical conflict) : Then for some N  N : But then derive (using reachability + derivability of N) : s  * x N   x    * x a   * x a y s  * x N   x  ’   * x a   * x a y N    * a , N   ’  * a , L (  )  L (  ’ )  { a }   G  G  G unambiguous G ambiguous  G  G

20. // Proof (Lemma 1b): “  ” (cont’d) Assume “ ” (horizontal conflict) : Then for some N  N : But then derive (using reachability + derivability of N) : s  * v N   v     * v x    * v x a y   * v x a y w s  * v N   v     * v x a    * v x a y   * v x a y w N    , L (  ) L (  )    x,y   * :  a   + : x,x a  L (  )  y, a y  L (  ) i.e.  

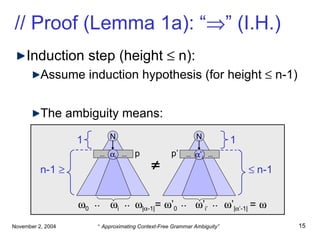
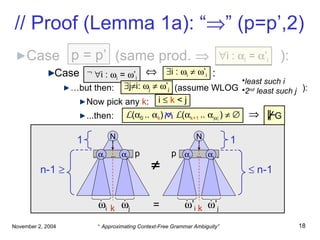
21. // (Over-)Approximation (A) (Over-)Approximation A : E*  P (  *) A decidable  “ ” and “ ” decidable on co-dom( A ) Approximated vertical ambiguity: Approximated horizontal ambiguity:   E* : L (  )  A (  )  n  N :  ,  ’   (n) : A (  )  A (  ’) =  A A  n  N:    (n):  i  [1..|  |-1]: A (  0 ..  i-1 ) A (  i ..  |  |-1 ) =   G G    

22. // Ambiguity Approximation Theorem 2: Proof : “ Conflicts w/ smaller sets  conflicts w/ larger sets”:   G unambiguous A (  )  A (  ) =   L (  )  L (  ) =  A (  ) A (  ) =   L (  ) L (  ) =  A A    A A G G G G G G    

23. // Compositionality (of A’s) Colloary 3: Proof: Follows from definition [omited…] i.e. “Approximations are compositional ”!: A , A’ decidable (over-)approximations  A  A’ decidable (over-)approximation unambiguous ambiguous unambiguous ambiguous unambiguous ambiguous A A’ A  A’ 

24. // Choice(s) of A? A  * (  ) =  * (constant) Worst approximation … but safe approximation! Useless: “ Cannot determine that any grammars are unambiguous” unambiguous ambiguous worst approximation

25. // Choice(s) of A? (cont’d) A MN (  ) = [Mohri-Nederhof](  ) CFG  DFA (NFA) Approximation Properties of this “ Black-box ”: Good (over-)approximation! Works on language , L (G); not on grammatical structure , G Approximation parameterizable : E.g. unfold nonterminals “n” times “ Regular Approximation of Context-Free Grammars through Transformation” [Mohri-Nederhof, 2000] Black-box

26. // Decidability (of A MN ) “  ” decidable (using DFAs) O(|X NFA ||Y NFA |) “ ” decidable (using DFAs) O(|X NFA ||Y NFA |) A MN decidable With potential counterexamples (using DFAs) X  Y =  X Y =    G unambiguous A MN A MN    

27. For X,Y regular languages: All overlappings, “x a y”, as DFAs; variant of “  ” construction! // Decision Algorithm for (X Y)  X NFA Y NFA [X;Y] NFA   a  path : X NFA Y NFA [X;Y] NFA a a x y x a y a a X Y Y X X  Y   

28. // Three Approximation Answers Y! : “ G definitely not ambiguous ”! “ ? / D ? ”: “ ? ”: “ Don’t know ”? … could not find any potential counterexamples . “ D ? ”: “ Don’t know ” – look at over-approx, D? … and here are all potential counterexamples Note : some strings do not even parse! Improve : Parse S  FIN D  subset of real counterexamples True answer

29. // Regaining Lost Precision! Now parse all counterexamples ! i.e. parse DFA, D DFA : 1) i.e. construct: Decidable in O(|D||G|) 2) Decide emptyness on C: Decidable in O(|C| = |D||G|) Only potential counterexamples that parse! L (C CFG ) = L (D DFA )  L (G CFG ) L (C CFG ) = 

30. // Three Approximation Answers Y! : “ G definitely not ambiguous ”! “ ? / C ? ”: “ ? ”: “ Don’t know ”? … could not find any counterexamples. “ C ? ”: “ Don’t know ” – look at over-approx, C? … and here are all potential counterexamples Note : all strings actually parse (maybe not ambiguously)! Improve : extract finite under-approximation...? True answer

31. [Mohri-Nederhof]: O(n 2 vh) Vertical Amb: O(n 3 v 4 h 4 ) Horizontal Amb: O(n 3 v 3 h 5 ) Total: O(n 3 v 3 h 4 (v+h))  O(g 5 ) // Asymptotic (Time) Complexity N 1 : e 1,1 … e a,1 : … : e 1,p … e a,p h n v n = | N | v = max{|  (N)|, N  N } h = max{|  |,  (N), N  N } g = nvh = |G|

32. // Related Work (Dynamic) Dynamic disambiguation : “ Disambiguation-by-convention”: Longest match, most specific match, … Customizable: [Bison v. 1.5+]: %dprec , %merge [ASF+SDF]: “disambiguation filters” Dynamic ambiguity interception : GLR ([Tomita], [Early], [Bison], [ASF+SDF], …)

33. // Related Work (Static) Static disambiguation : “ Disambiguation-by-convention”: First match, most specific match, … Customizable: [Yacc]: %left , %right , %nonassoc , %prec Static ambiguity interception : LL(k), [LA-]LR(k), … Our work goes here (but for GLR)!

34. // Implementation disamb (Java) In progress…!

35. // Assessment Quality of approximation ~ ~ Quantity of false-positives Precision: Our \ LR(k) ? LR(k) \ Our ? False-positives ? Characterize “ ? ” / “ N ? ” In terms of grammatical structure ? Efficiency (in practise…) In progress…!

36. // Example: Expression chains … !? E -> E + T -> T T -> T * F -> F F -> ( E ) -> x

37. // Example: Balancing Structures Nasty: Requires: Unbounded memory (# x’es) i.e. CFG structure Unbounded lookahead i.e. any finite k is insufficient  False-positives! S -> A A A -> x A x -> y xxyxx xyx Example string:

38. // Future Work Permit With disambiguating conventions for: Associativity Precedence Parsing optimization: Exploit compile-time analysis information at runtime … E -> E  E

39. // Conclusion But wait, there’s more… “ Approximating Context-Free Grammar Ambiguity” Context-free grammar ambiguity is undecidable. However, just because it’s undecidable, doesn’t mean there aren’t (good) approximations! Indeed, the whole area of static analysis works on “side-stepping undecidability” . We exhibit a characterization of context-free ambiguity which induces a whole framework for (over-)approximation. In particular, we give an approximation based on the [Mohri-Nederhof, 2000] regular approximation of context-free grammars and show how to boost the precision even further.

40. // Lessons Learned Framework: Plug in your favorite (over-)approximation of L (  ) Even take intersection of them: A =  i A i Approximation closed under intersection Methodology: Just because it’s undecidable doesn’t mean there aren’t (good) approximations Quantity of false-positives (practically motivated) What to do with false-positives (pratically motivated) Don’t be scared of undecidability

41. [bonus slides]

42. // Membership: Decidable! Membership (aka. “parsing” ): Given    * : “ Is the string,  , in the language of G”: Algorithms: LL(k) O(|  |) [LA-]LR(k) O(|  |) GLR O(|  | 3 ) …   L (G)

43. The ambiguity problem for [X;Y]... In fact, already a problem if x’ “goes too far”: Thus, we only have a problem if (“X eats into Y”): Essentially disambiguation by picking longest match // Parsing Greedily Left-to-Right x y x’ y’ x y - (“too little”): Not possible (due to greediness) ... may occur in 2 cases: - (“too much”): Only this is a problem!  X  X;( prefix(Y) \ {  } )    X Y  x’ y’