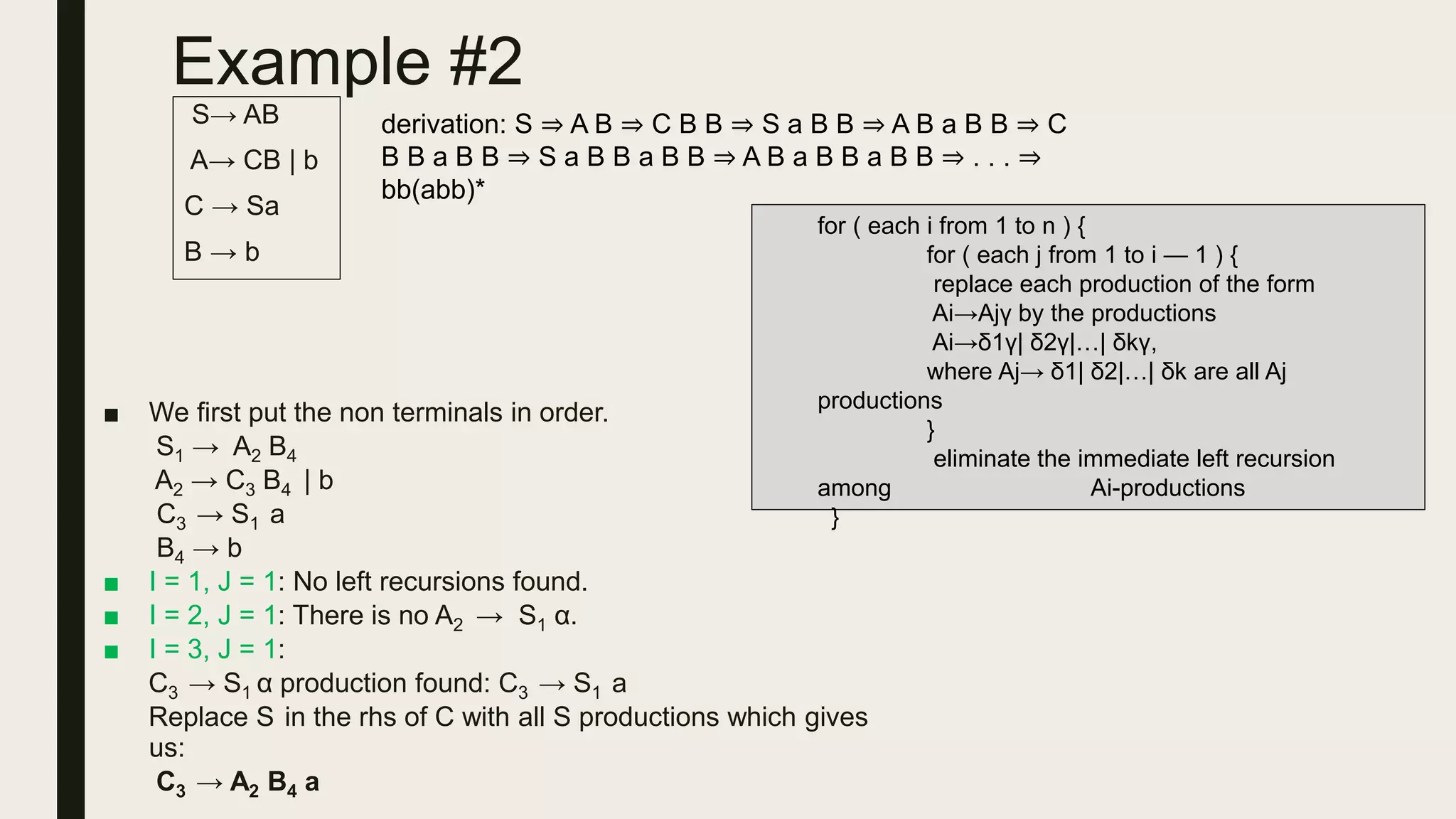
The document discusses the use of regular expressions in defining the lexical syntax of programming languages, emphasizing their simplicity and efficiency compared to grammars. It also covers concepts such as eliminating ambiguity, left recursion, and left factoring in grammars, along with examples and algorithms to achieve these transformations. Additionally, it mentions constructs that cannot be expressed in context-free grammars, highlighting the need for context-sensitive rules in certain programming scenarios.

1. WRITING
GRAMMAR

2. Grammars
■ capable of describing most syntax of
programming languages

3. "Why use regular expressions to
define the lexical syntax of a
language?"
■ Separating the syntactic structure of a language into lexical and non lexical parts
provides a convenient way of modularizing the front end of a compiler into two
manageable-sized components.
■ The lexical rules of a language are frequently quite simple, and to describe them
we do not need a notation as powerful as grammars
■ Regular expressions generally provide a more concise and easier-to-understand
notation for tokens than grammars.
■ More efficient lexical analyzers can be constructed automatically from regular
expressions than from arbitrary grammars.

4. ELIMINATING
AMBIGUITY
A grammar that produces more than one parse tree for some
sentence is said to be ambiguous.

5. Example:
E → E or E |
E and E |
not E |
True |
False
For the string : True and False or True
E E
/ | / |
E and E E or E
| / | / | |
True E or E E and E
True
| | | |
False True True False
It has more than one parse trees. Therefore the
grammar is ambiguous.
Ambiguity Eliminated:
E → E or F | F
F→ F and G | G
G → Not G | True | False
E
/ |
E or F
/ | |
F and G G
| | |
G False True
|
True

6. ELIMINATION OF
LEFT RECURSION
A grammar is left recursive if it takes the
form A → Aα | β

7. Two Cases
■ Immediate Left Recursion - A → A α left hand side symbol is the same as first
right hand side symbol.
■ Indirect Left Recursion - A → B α → . . . → A β A extends via intermediate steps
into another derivation part that starts with A.

8. Example #1:
■ Determine which is left
recursive. Note: A grammar is
left recursive if the variable
appears as prefix on one or
more of its productions. (A →
Aα | β)
■ Change the LR production into
A→ βA’
A’→ αA’|ε
■ Continue until there are no LR
Productions left.
E → E or F | F
F→ F and G | G
G → Not G | True | False
E → FE’
E’ → orFE’ | ε
F→ F and G | G
G → Not G | True | False
E → FE’
E’ → or FE’ | ε
F→ GF’
F’ → and GF’ | ε
G → Not G | True | False

9. Algorithm
■ Arrange the nonterminals in some order Ai,Az,... ,An.
for ( each i from 1 to n ) {
for ( each j from 1 to i — 1 ) {
replace each production of the form
Ai→Ajγ by the productions
Ai→δ1γ| δ2γ|…| δkγ,
where Aj→ δ1| δ2|…| δk are all Aj – productions
}
eliminate the immediate left recursion among Ai-productions
}
Input → grammar G with no cycles or ε-productions
Output → an equivalent grammar with no left recursion
After the first
iteration, this block
will replace all found
Ai → Ajy productions
where i>j which
eliminates indirect
LR

10. Example #2
■ We first put the non terminals in order.
S1 → A2 B4
A2 → C3 B4 | b
C3 → S1 a
B4 → b
■ I = 1, J = 1: No left recursions found.
■ I = 2, J = 1: There is no A2 → S1 α.
■ I = 3, J = 1:
C3 → S1 α production found: C3 → S1 a
Replace S in the rhs of C with all S productions which gives
us:
C3 → A2 B4 a
for ( each i from 1 to n ) {
for ( each j from 1 to i — 1 ) {
replace each production of the form
Ai→Ajγ by the productions
Ai→δ1γ| δ2γ|…| δkγ,
where Aj→ δ1| δ2|…| δk are all Aj
productions
}
eliminate the immediate left recursion
among Ai-productions
}
S→ AB
A→ CB | b
C → Sa
B → b
derivation: S ⇒ A B ⇒ C B B ⇒ S a B B ⇒ A B a B B ⇒ C
B B a B B ⇒ S a B B a B B ⇒ A B a B B a B B ⇒ . . . ⇒
bb(abb)*

11. Cont. Example #2
■ I = 3, J = 2: C → A α rule found.
Apply same step.
C3 → C3 B4 B4 a | b B4 a
We get out of the inner loop where all immediate LRs are
discovered.
C is left recursive so eliminate.
New derived grammar:
C3 → b B4 a C3’
C3’ → B4 B4 a C3’ | ε
Current grammar:
S1 → A2 B4
A2 → C3 B4 | b
C3 → A2 B4 a
B4 → b
for ( each i from 1 to n ) {
for ( each j from 1 to i — 1 ) {
replace each production of the form
Ai→Ajγ by the productions
Ai→δ1γ| δ2γ|…| δkγ,
where Aj→ δ1| δ2|…| δk are all Aj productions
}
eliminate the immediate left recursion among
Ai-productions
}
Final Grammar:
S → A B
A → C B | b
C → bBaC’
C’ → BBaC’ | ε

12. LEFT FACTORING
"factoring out" prefixes which are common to two or more
productions

13. Method & Example:
■ For each non-terminal A find the longest prefix α to two or more alternatives
statement → identifier := exp | identifier ( exp-list ) | other
■ Replace A-productions A→ αβ1 | αβ2 |…| αβn | γ by
A→αA’ | γ
A’→ β1 | β2 |…| βn
■ Repeat if necessary.
final left factored grammar:
statement → identifier statement’ | other
statement’ → := exp | (exp-list)
statement → identifier := exp | identifier ( exp-list ) | other
Input ◦ grammar G
Output ◦ equivalent left-factored grammar

14. Example #2
■ Left factor S:
S → TS’
S ‘ → +S | ε
■ Left factor T:
T → UT’
T’ → * T | ε
S → T + S | T
T → U * T | U
U → (S) | V
V → 0 | 1 | ... | 9
Final Left Factored Grammar:
S → TS’
S ‘ → +S | ε
T → UT’
T’ → * T | ε
U → (S) | V
V → 0 | 1 | ... | 9

15. NON CONTEXT FREE
LANGUAGE
CONSTRUCTS

16. Declaration before Use
L1 = {wcw|w is {a,b}+}
where the first w is declaration and the second represents its use.
■ When a statement for use of variable is generated, it requires context or
knowledge of whether the variable used was defined before. If this Declaration
rule is satisfied, it is only then that the statement will be valid to the program.
This makes the language context sensitive.
Parameter No. Matching
L2 = {an bm cn dm| n,m >=1}
Here a and b could represent the formal-parameter lists of two functions declared while c and
d represent the actual-parameter lists in calls to these two functions.
■ The requirement to match the number of arguments of the calls to the
declarations for a generated language to be valid makes it non context free.