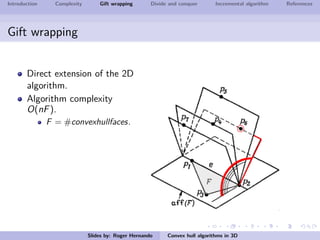
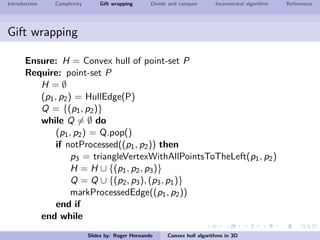
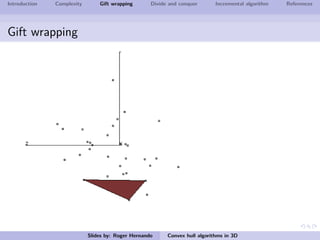
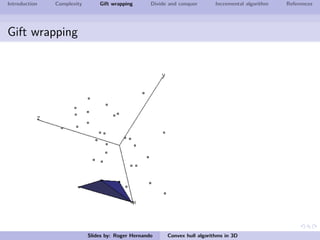
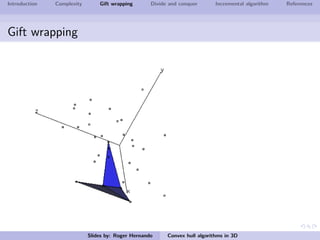
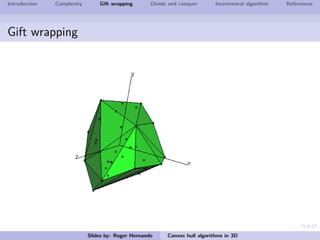
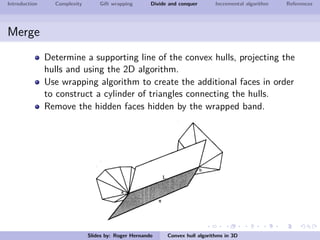
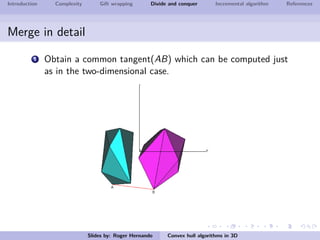
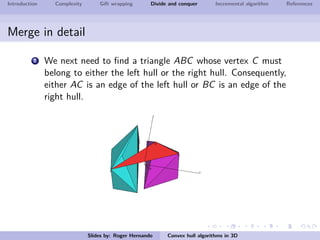
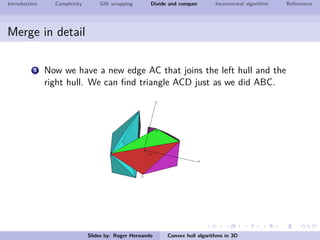
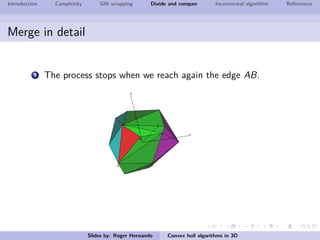
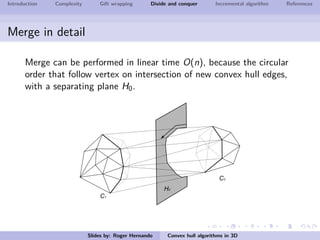
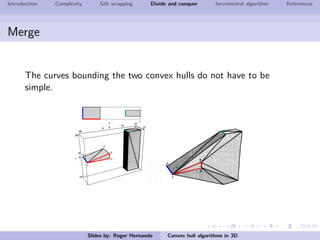
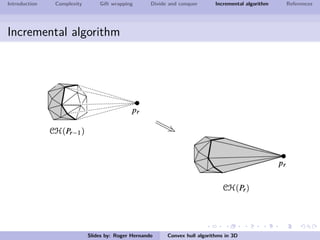
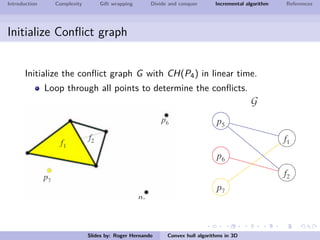
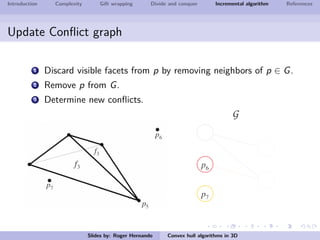
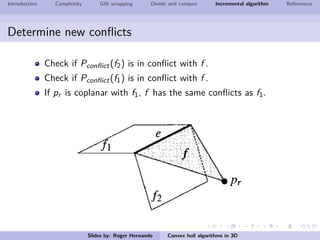
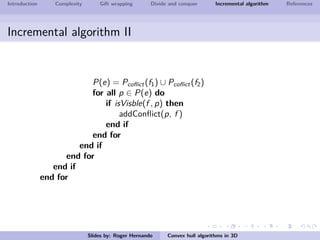
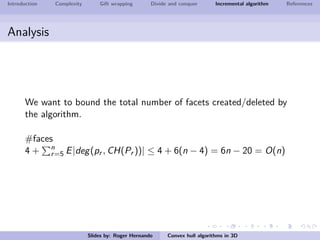
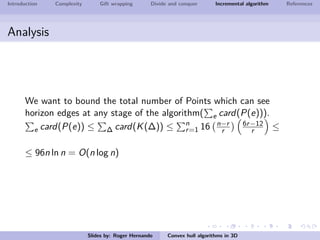
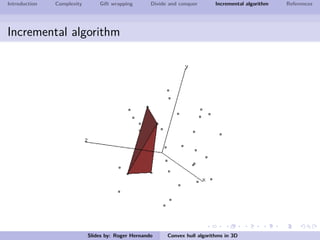
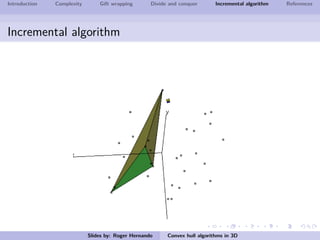
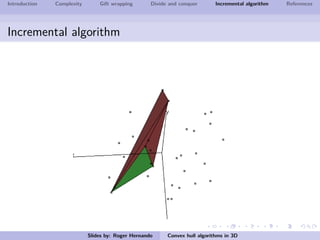
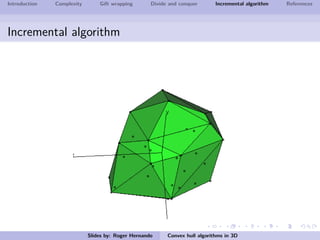
The document discusses several algorithms for computing the 3D convex hull of a set of points: gift wrapping, divide and conquer, and incremental. Gift wrapping directly extends the 2D algorithm and has complexity O(nF) where F is the number of faces. Divide and conquer recursively splits the point set into halves, computes the convex hulls, and merges them in O(n log n) time. The incremental algorithm maintains a conflict graph to efficiently find the visible faces from each new point in O(n log n) time.

1. Convex hull algorithms in 3D
Slides by: Roger Hernando

2. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Outline
1 Introduction
2 Complexity
3 Gift wrapping
4 Divide and conquer
5 Incremental algorithm
6 References
Slides by: Roger Hernando Convex hull algorithms in 3D

3. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Problem statement
Given P: set of n points in 3D.
Convex hull of P: CH(P), the
smallest polyhedron s.t. all
elements of P on or in the interior
of CH(P).
Slides by: Roger Hernando Convex hull algorithms in 3D

4. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Visibility test
A point is visible from a face?
The point is above or below the supporting plane of the face.
The volume of the tetrahedron is positive or negative.
Slides by: Roger Hernando Convex hull algorithms in 3D

5. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Complexity of the 3D Convex Hull
Euler’s theorem:
V − E + F = 2
Triangle mesh 3F = 2E:
V − E +
2E
3
= 2 ⇒ E = 3V − 6
Slides by: Roger Hernando Convex hull algorithms in 3D

6. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Complexity of the Convex Hull
Given a set S of n points in Rn what is maximum #edges on
CH(S)?
Bernard Chazelle [1990]: CH of n points in Rd in optimal
worst-case is O n log n + n
d
2 . Bound by Seidel[1981].
Slides by: Roger Hernando Convex hull algorithms in 3D

7. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Direct extension of the 2D
algorithm.
Algorithm complexity
O(nF).
F = #convexhullfaces.
Slides by: Roger Hernando Convex hull algorithms in 3D

8. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Ensure: H = Convex hull of point-set P
Require: point-set P
H = ∅
(p1, p2) = HullEdge(P)
Q = {(p1, p2)}
while Q = ∅ do
(p1, p2) = Q.pop()
if notProcessed((p1, p2)) then
p3 = triangleVertexWithAllPointsToTheLeft(p1, p2)
H = H ∪ {(p1, p2, p3)}
Q = Q ∪ {(p2, p3), (p3, p1)}
markProcessedEdge((p1, p2))
end if
end while
Slides by: Roger Hernando Convex hull algorithms in 3D

9. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Slides by: Roger Hernando Convex hull algorithms in 3D

10. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Slides by: Roger Hernando Convex hull algorithms in 3D

11. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Slides by: Roger Hernando Convex hull algorithms in 3D

12. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Slides by: Roger Hernando Convex hull algorithms in 3D

13. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Slides by: Roger Hernando Convex hull algorithms in 3D

14. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Gift wrapping
Slides by: Roger Hernando Convex hull algorithms in 3D

15. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Divide and conquer
The same idea of the 2d algorithm.
1 Split the point-set P in two sets.
2 Recursively split, construct CH, and merge.
Merge takes O(n) ⇒ Algorithm complexity O(n log n).
Slides by: Roger Hernando Convex hull algorithms in 3D

16. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Divide and conquer
Ensure: Convex hull of point-set P
Require: point-set P(sorted by certain coord)
function divideAndConquer(P)
if |P| ≤ x then
return incremental(P)
end if
(P1, P2) = split(P)
H1 = divideAndConquer(P1)
H2 = divideAndConquer(P2)
return merge(H1, H2)
end function
Slides by: Roger Hernando Convex hull algorithms in 3D

17. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge
Determine a supporting line of the convex hulls, projecting the
hulls and using the 2D algorithm.
Use wrapping algorithm to create the additional faces in order
to construct a cylinder of triangles connecting the hulls.
Remove the hidden faces hidden by the wrapped band.
Slides by: Roger Hernando Convex hull algorithms in 3D

18. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge in detail
1 Obtain a common tangent(AB) which can be computed just
as in the two-dimensional case.
Slides by: Roger Hernando Convex hull algorithms in 3D

19. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge in detail
2 We next need to find a triangle ABC whose vertex C must
belong to either the left hull or the right hull. Consequently,
either AC is an edge of the left hull or BC is an edge of the
right hull.
Slides by: Roger Hernando Convex hull algorithms in 3D

20. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge in detail
3 Now we have a new edge AC that joins the left hull and the
right hull. We can find triangle ACD just as we did ABC.
Slides by: Roger Hernando Convex hull algorithms in 3D

21. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge in detail
3 The process stops when we reach again the edge AB.
Slides by: Roger Hernando Convex hull algorithms in 3D

22. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge in detail
Merge can be performed in linear time O(n), because the circular
order that follow vertex on intersection of new convex hull edges,
with a separating plane H0.
Slides by: Roger Hernando Convex hull algorithms in 3D

23. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge
The curves bounding the two convex hulls do not have to be
simple.
Slides by: Roger Hernando Convex hull algorithms in 3D

24. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge I
Ensure: C is the convex hull of H1, H2
Require: Convex hulls H1, H2
function merge(H1, H2)
C = H1 ∪ H2
e(p1, p2) = supportingLine(H1, H2)
L = e
repeat
p3 = giftWrapAroundEdge(e)
if p3 ∈ H1 then
e = (p2, p3)
else
e = (p1, p3)
end if
C = C ∪ {(p1, p2, p3)}
Slides by: Roger Hernando Convex hull algorithms in 3D

25. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Merge II
until e = L
discardHiddenFaces(C)
end function
Slides by: Roger Hernando Convex hull algorithms in 3D

26. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
Slides by: Roger Hernando Convex hull algorithms in 3D

27. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
1 Create tetrahedron(initial CH).
pick 2 points p1 and p2.
pick a point not lying on the line p1p2.
pick a point not lying on the plane p1p2p3(if not found use a
2D algorithm).
2 Randomize the remaining points P.
3 For each pi ∈ P, add pi into the CHi−1
if pi lies inside or on the boundary of CHi−1 then do nothing.
if pi lies outside of CHi−1 insert pi .
Slides by: Roger Hernando Convex hull algorithms in 3D

28. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
Ensure: C Convex hull of point-set P
Require: point-set P
C = findInitialTetrahedron(P)
P = P − C
for all p ∈ P do
if p outside C then
F = visbleFaces(C, p)
C = C − F
C = connectBoundaryToPoint(C, p)
end if
end for
Slides by: Roger Hernando Convex hull algorithms in 3D

29. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Find visible region
Naive:
Test every face for each point O(n2
).
Conflict graph:
Maintain information to aid in determining visible facets from
a point.
Slides by: Roger Hernando Convex hull algorithms in 3D

30. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Conflict graph
Relates unprocessed points with facets of CH they can see.
Bipartite graph.
pt unprocessed points.
f faces of the convex hull.
conflict arcs, point pi sees fj .
Maintain sets:
Pconflict(f ), points that can see f .
Fconflict(p), faces visible from p(visible
region deleted after insertion of p).
At any step of the algorithm, we know all
conflicts between the remaining points and
facets on the current CH.
Slides by: Roger Hernando Convex hull algorithms in 3D

31. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Initialize Conflict graph
Initialize the conflict graph G with CH(P4) in linear time.
Loop through all points to determine the conflicts.
Slides by: Roger Hernando Convex hull algorithms in 3D

32. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Update Conflict graph
1 Discard visible facets from p by removing neighbors of p ∈ G.
2 Remove p from G.
3 Determine new conflicts.
Slides by: Roger Hernando Convex hull algorithms in 3D

33. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Determine new conflicts
Check if Pconflict(f2) is in conflict with f .
Check if Pconflict(f1) is in conflict with f .
If pr is coplanar with f1, f has the same conflicts as f1.
Slides by: Roger Hernando Convex hull algorithms in 3D

34. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm I
Ensure: C Convex hull of point-set P
Require: point-set P
C = findInitialTetrahedron(P)
initializeConflictGraph(P, C)
P = P − C
for all p ∈ P do
if Fconflict(p) = ∅ then
delete(Fconflict(p), C)
L = borderEdges(C)
for all e ∈ L do
f = createNewTriangularFace(e, p)
f = neighbourFace(e)
addFaceToG(f )
if areCoplanar(f , f ) then
Pconflict(f ) = Pconflict(f )
else
Slides by: Roger Hernando Convex hull algorithms in 3D

35. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm II
P(e) = Pcoflict(f1) ∪ Pcoflict(f2)
for all p ∈ P(e) do
if isVisble(f , p) then
addConflict(p, f )
end if
end for
end if
end for
end if
end for
Slides by: Roger Hernando Convex hull algorithms in 3D

36. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Analysis
We want to bound the total number of facets created/deleted by
the algorithm.
#faces
4 + n
r=5 E|deg(pr , CH(Pr ))| ≤ 4 + 6(n − 4) = 6n − 20 = O(n)
Slides by: Roger Hernando Convex hull algorithms in 3D

37. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Analysis
We want to bound the total number of Points which can see
horizon edges at any stage of the algorithm( e card(P(e))).
Define:
Set of active configurations τ(S).
A flap ∆ = (p, q, s, t).
∆ ∈ τ(S)all edges in the flap are edges of the CH(S).
Set K(∆) points which have the flap ∆ as horizon edge.
Slides by: Roger Hernando Convex hull algorithms in 3D

38. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Analysis
We want to bound the total number of Points which can see
horizon edges at any stage of the algorithm( e card(P(e))).
e card(P(e)) ≤ ∆ card(K(∆)) ≤ n
r=1 16 n−r
r
6r−12
r ≤
≤ 96n ln n = O(n log n)
Slides by: Roger Hernando Convex hull algorithms in 3D

39. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
Slides by: Roger Hernando Convex hull algorithms in 3D

40. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
Slides by: Roger Hernando Convex hull algorithms in 3D

41. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
Slides by: Roger Hernando Convex hull algorithms in 3D

42. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
Slides by: Roger Hernando Convex hull algorithms in 3D

43. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
Incremental algorithm
Slides by: Roger Hernando Convex hull algorithms in 3D

44. Introduction Complexity Gift wrapping Divide and conquer Incremental algorithm References
References I
Applet:
http://www.cse.unsw.edu.au/ lambert/java/3d/hull.htm
M. de Berg, O. Cheong, M. van Kreveld, M. Overmars,
Computational Geometry Algorithms and Applications
J. O’Rourke,Computational Geometry in C
Partha P. Goswami, Introduction to Computational Geometry
David M. Mount, Lecture notes.
Bernard Chazelle, An optimal convex hull algorith in any fixed
dimension
Alexander Wolf, Slides
Jason C. Yang, Slides
Peter Felkel, Slides
Slides by: Roger Hernando Convex hull algorithms in 3D