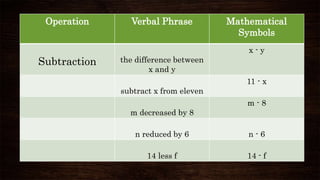
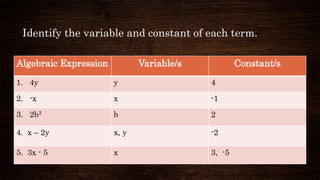
This document discusses algebraic expressions and polynomials. It defines key terms like variables, constants, and operations. It provides examples of algebraic expressions and identifies the variables and constants. It also defines polynomials as expressions with whole number exponents and restrictions. Examples are given to classify expressions as polynomials or not. The document also discusses classifying polynomials by number of terms and degree.

2. Let’s Prepare
Determine whether the underlined word or group of
words represent addition, subtraction, multiplication, or
division.
1. Eight added to a certain number = 8 + b
2. The quotient of a number and eleven =
𝑥
11
3. A number decreased by 5
4. Nine greater than a certain number
5. The product of four and x

3. Let’s Learn
The following examples show how verbal phrases
are translated to mathematical symbols.
Operation Verbal Phrase Mathematical
Symbols
Addition
the sum of 3 and 4 3 + 4
m increased by 5 m + 5
k added to 7 7 + k

4. Operation Verbal Phrase Mathematical
Symbols
Subtraction the difference between
x and y
x - y
subtract x from eleven
11 - x
m decreased by 8
m - 8
n reduced by 6 n - 6
14 less f 14 - f

5. Operation Verbal Phrase Mathematical
Symbols
Multiplication
the product of x and y xy
13 times y 13y
twice m 2m

6. Operation Verbal Phrase Mathematical
Symbols
Division
the ratio of m and n 𝑚
𝑛
The quotient of r and 5 𝑟
5
15 divided by x 15
𝑥

7. Understanding Algebraic Expression
An algebraic expression is a mathematical expression consist of
a variable, constant, or a combination of a variable and constant
related by at least one operation.
Variable – is a letter that can stand as a various number.
Constant – is a number, or symbol (3.14) that has a fixed value.
The following are the examples of an algebraic expression:
x -3 xy 5x -4bx2
x + y 2y x3 – 2 3b2 2𝑚
𝑛

8. Study the following:
Algebraic Expression Variable/s Constant/s
1. x = 1x x 1
2. xy x, y 1
3. 4x - 2 x 4, -2
4. 3y2 y 3
5. 2a + 3b a, b 2, 3

9. Identify the variable and constant of each term.
Algebraic Expression Variable/s Constant/s
1. 4y y 4
2. -x x -1
3. 2b3 b 2
4. x – 2y x, y -2
5. 3x - 5 x 3, -5

10. Polynomials
Polynomials are special kinds of algebraic expressions. These
expressions with a restriction that the exponents of a variables must be
whole numbers. A polynomial is a positive integral exponent.
The following are the restrictions of a polynomial:
• 1. No negative and fractional exponent in the variable
• 2. No variable under the radical sign (no variable serves as a
radicand 𝑥)
• 3. No variable in the denominator
2
𝑥

11. Polynomial Not Polynomial
x2
x-2
(the exponent of variable is negative)
y3
𝑦
1
3
(the exponent of the variable is a fraction)
y 4
4 𝑦
(the variable is under the radical sign)
3x
3𝑥
(the variable is under the radical sign)
𝑥
2
2
𝑥
(because the variable is at the denominator)

12. Identify whether is a polynomial or not.
Expression
1. 2x 6. a 2
2. 3xy 7.
2𝑥
𝑦
3. x-3 8. -y
4. x + 2-3 9. x + 3-2
5. a3 - 5 10.
𝑚𝑛
2

13. A. Classifying Polynomials According to
the Number of Terms
• term – an element in a polynomial separated by plus or minus
sign
Example Number of Terms Type of Polynomial
2x one (1) monomial
2a + b2 two (2) binomial
2r – 4s + 2 three (3) trinomial
2x3 + x2 + 5x - 12 more than 3 terms multinomial/polynomial

14. B. Classification of Polynomial According to Degree
– If a polynomial has only one variable, its degree is equal to
the highest power appearing in any of the terms.
– If the polynomial has more than one variable, its degree is
equal to the highest sum of the exponents of the variable in
any of the terms.
–A polynomial of a non-zero constant is considered to be a
polynomial of degree zero. The constant zero is called a
polynomial but without any degree.

15. Example:
Polynomial Degree
2x4 4
3a3 + 4a2
(exponent 3 is higher than exponent 2) 3
xy3
(Exponent 1 in variable x plus exponent 3 in y.
So, 1 + 3 = 4)
4
2a3b2c – bc2
(Exponent 3 in variable a, plus exponent 2 in variable b,
plus exponent 1 in variable c. So, 3 + 2 + 1 = 6)
6
4 0
-2 0