JL
Uploaded byJimbo Lamb
PDF, PPTX168 views

Algebra 2 Section 1-8

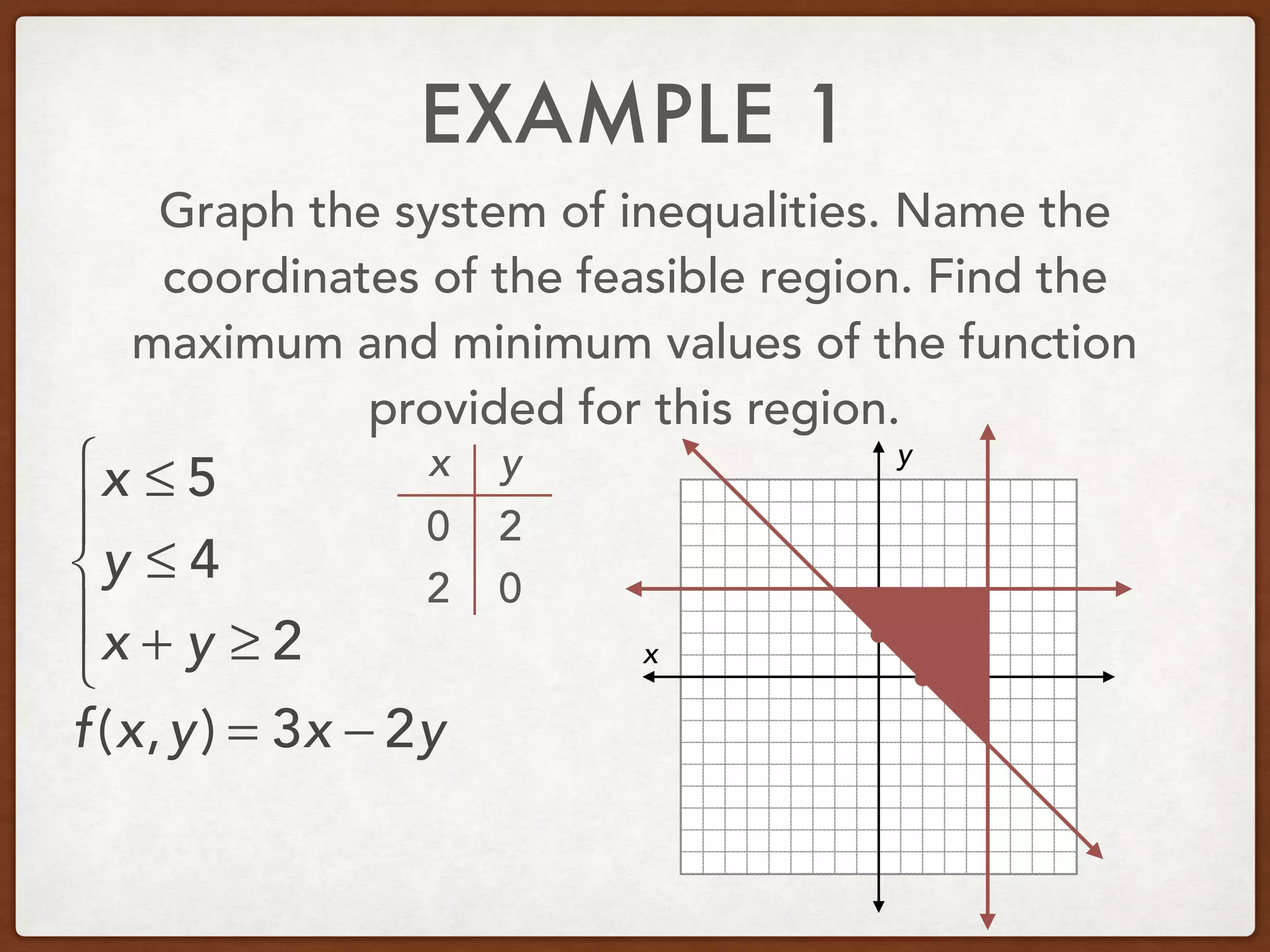
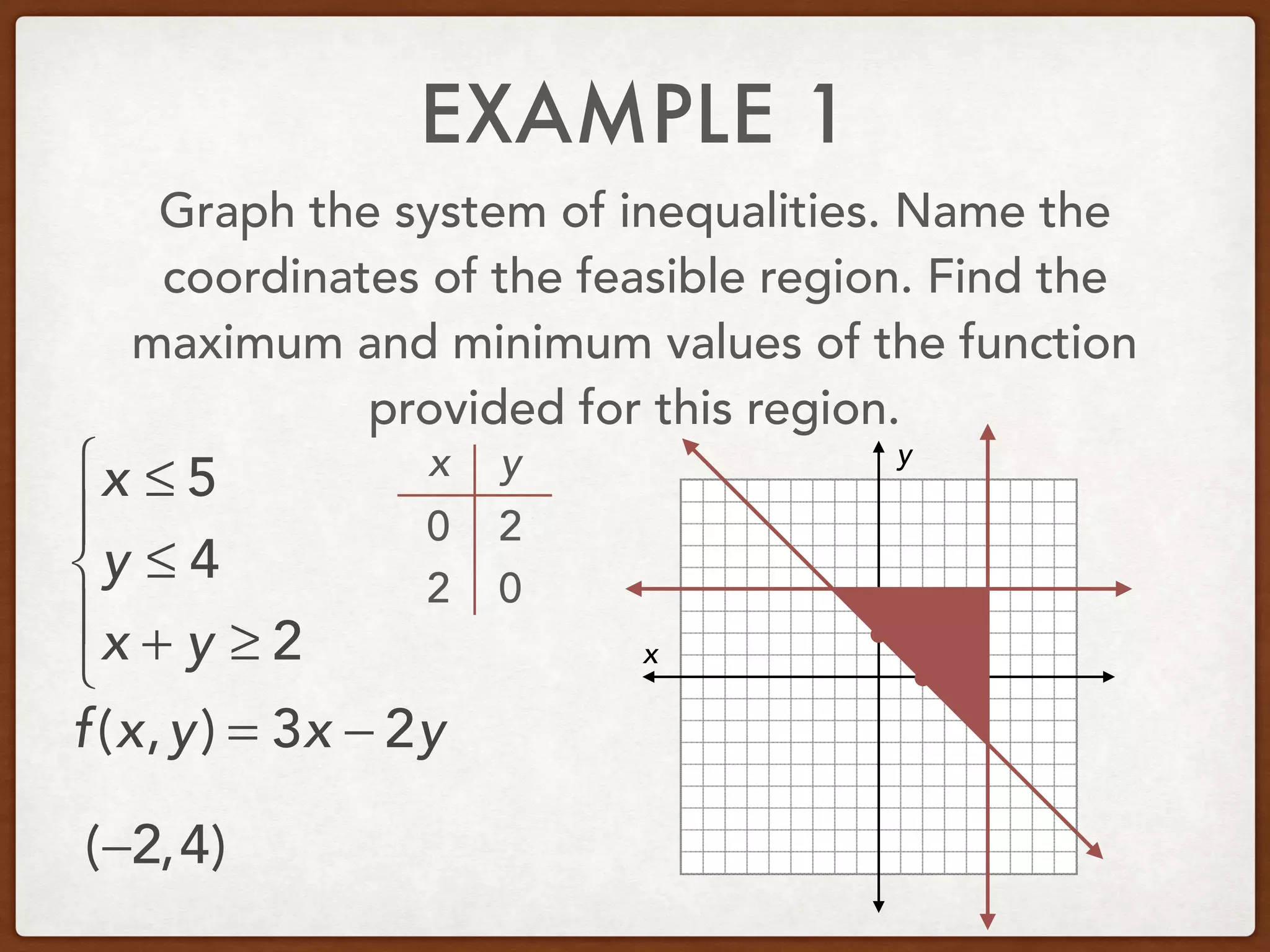
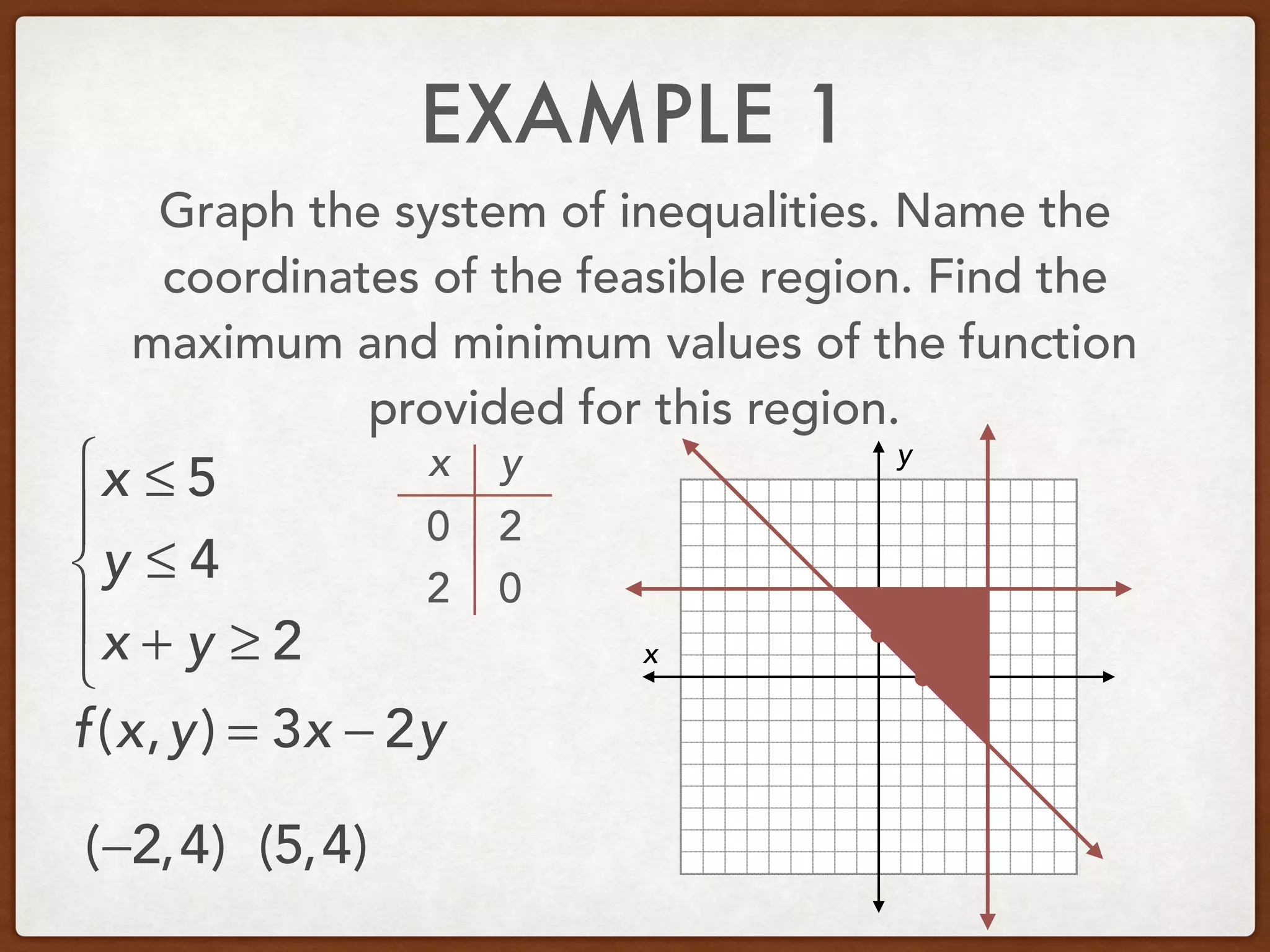
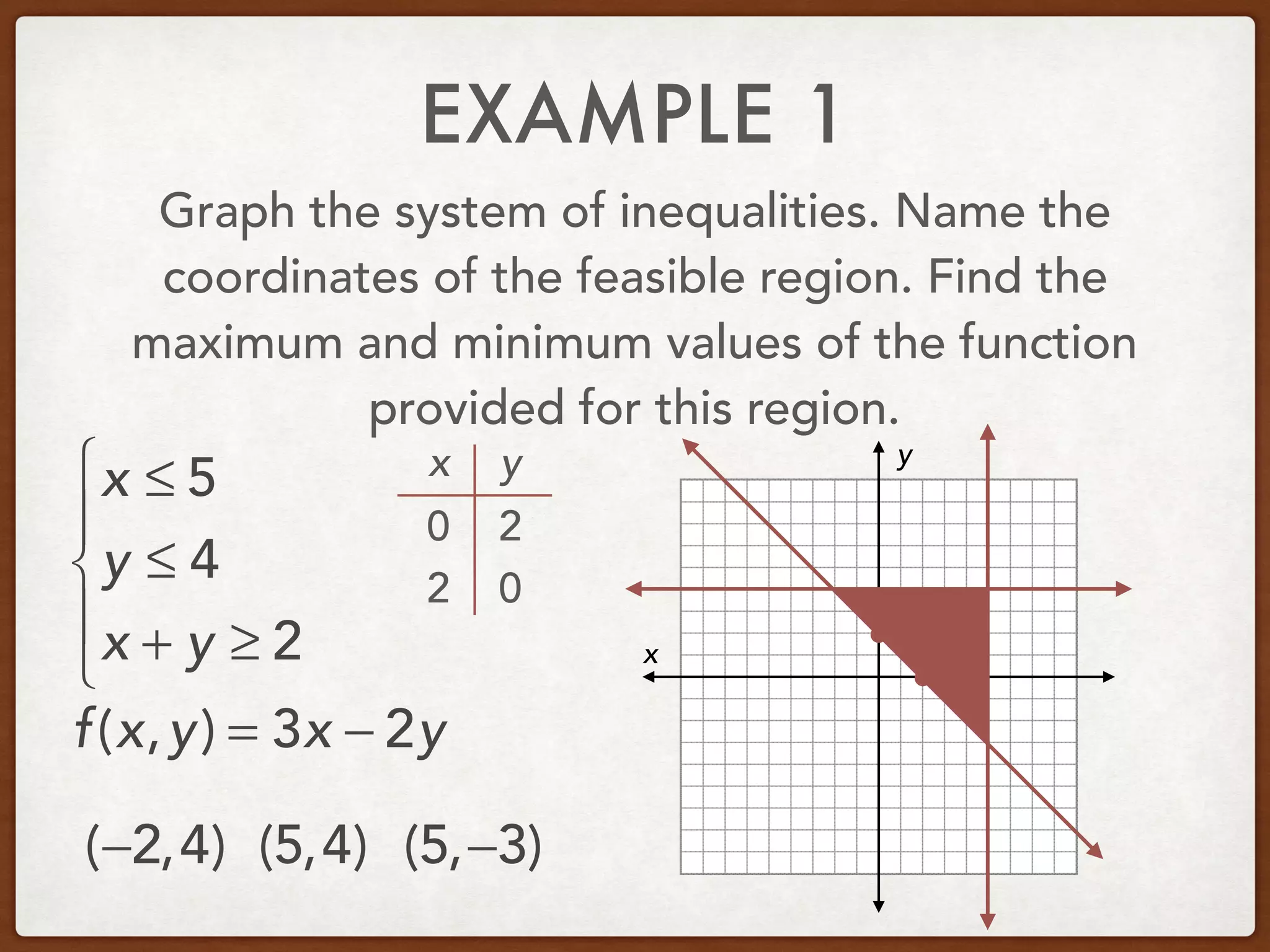
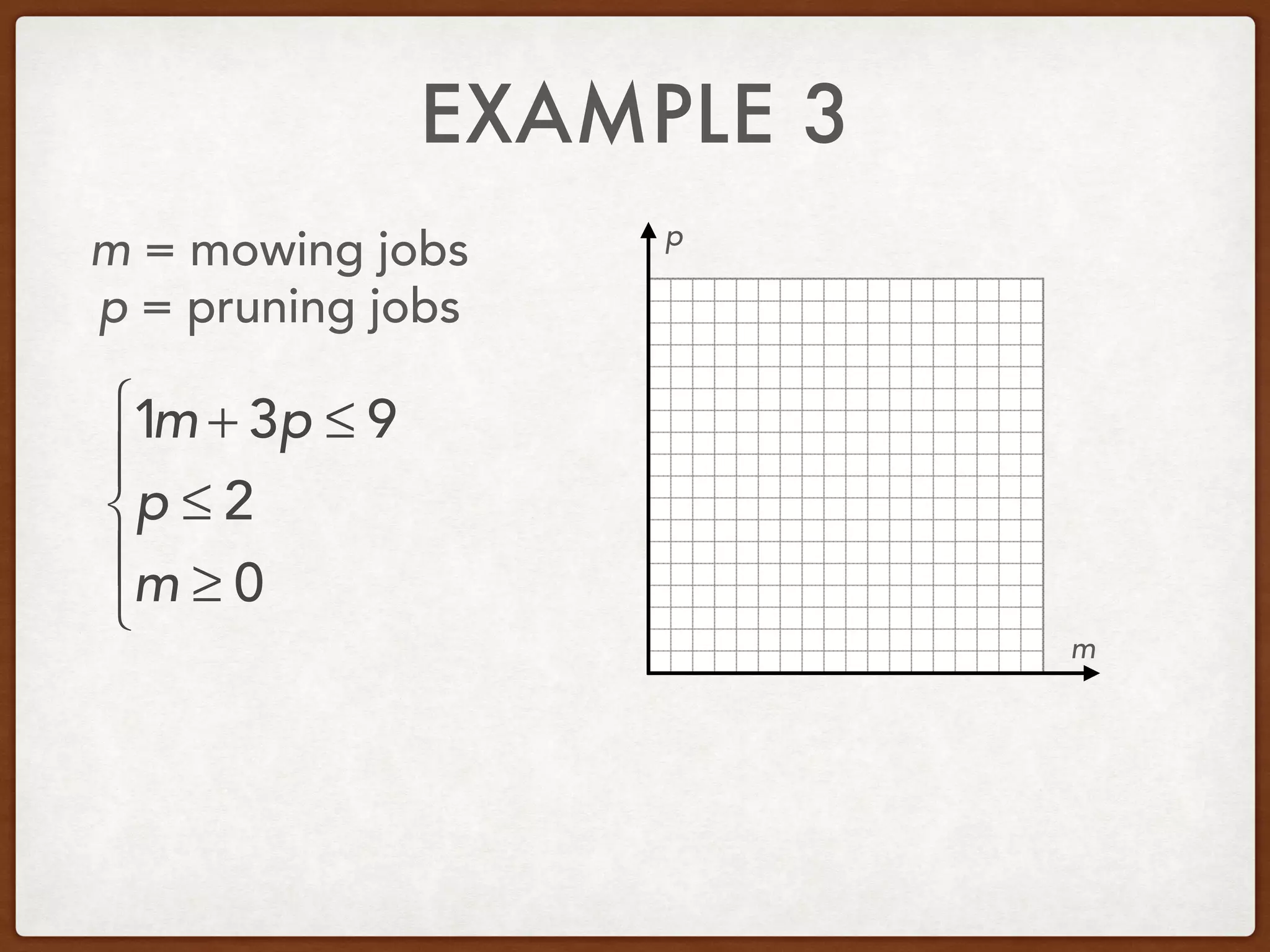
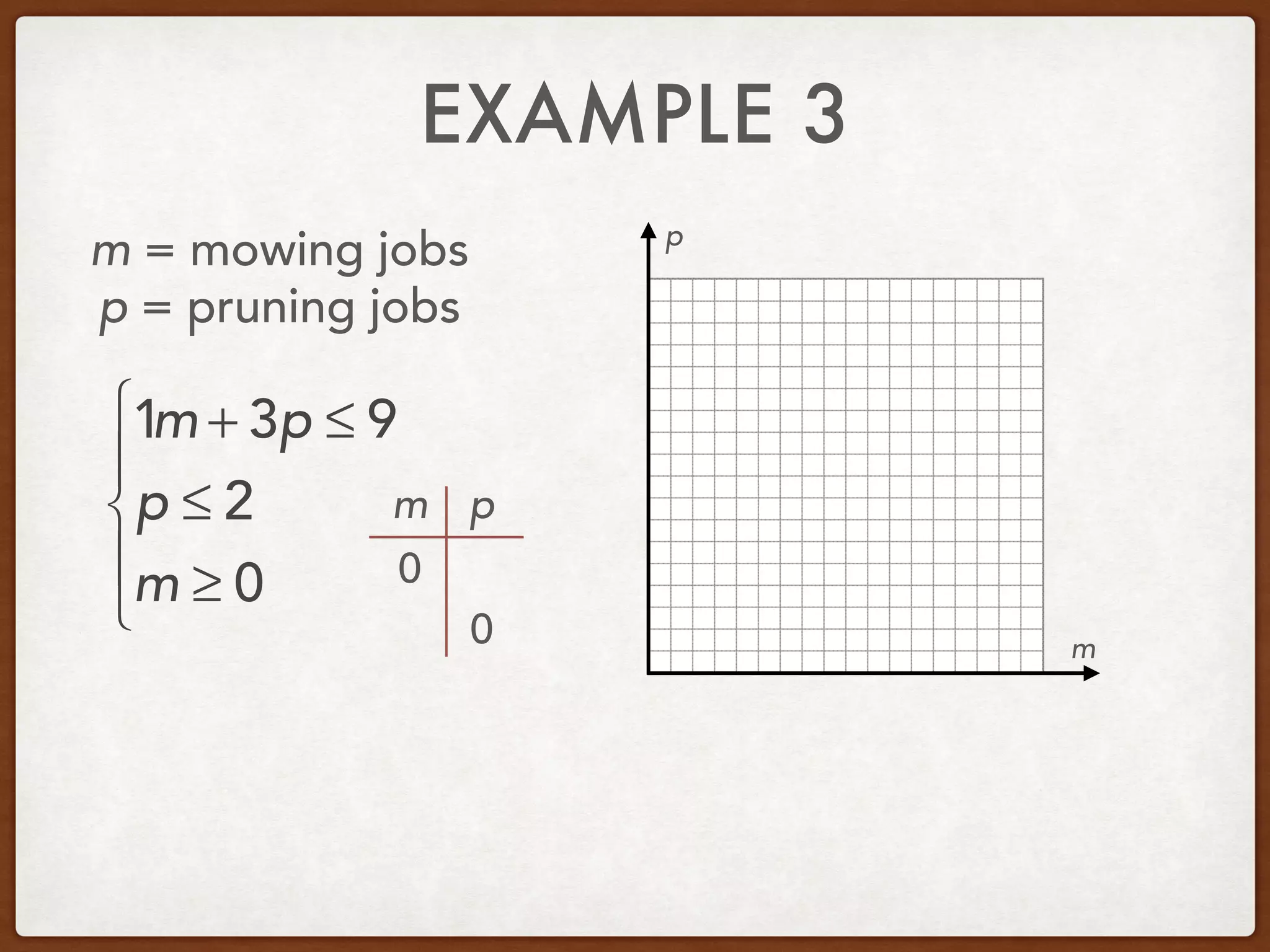
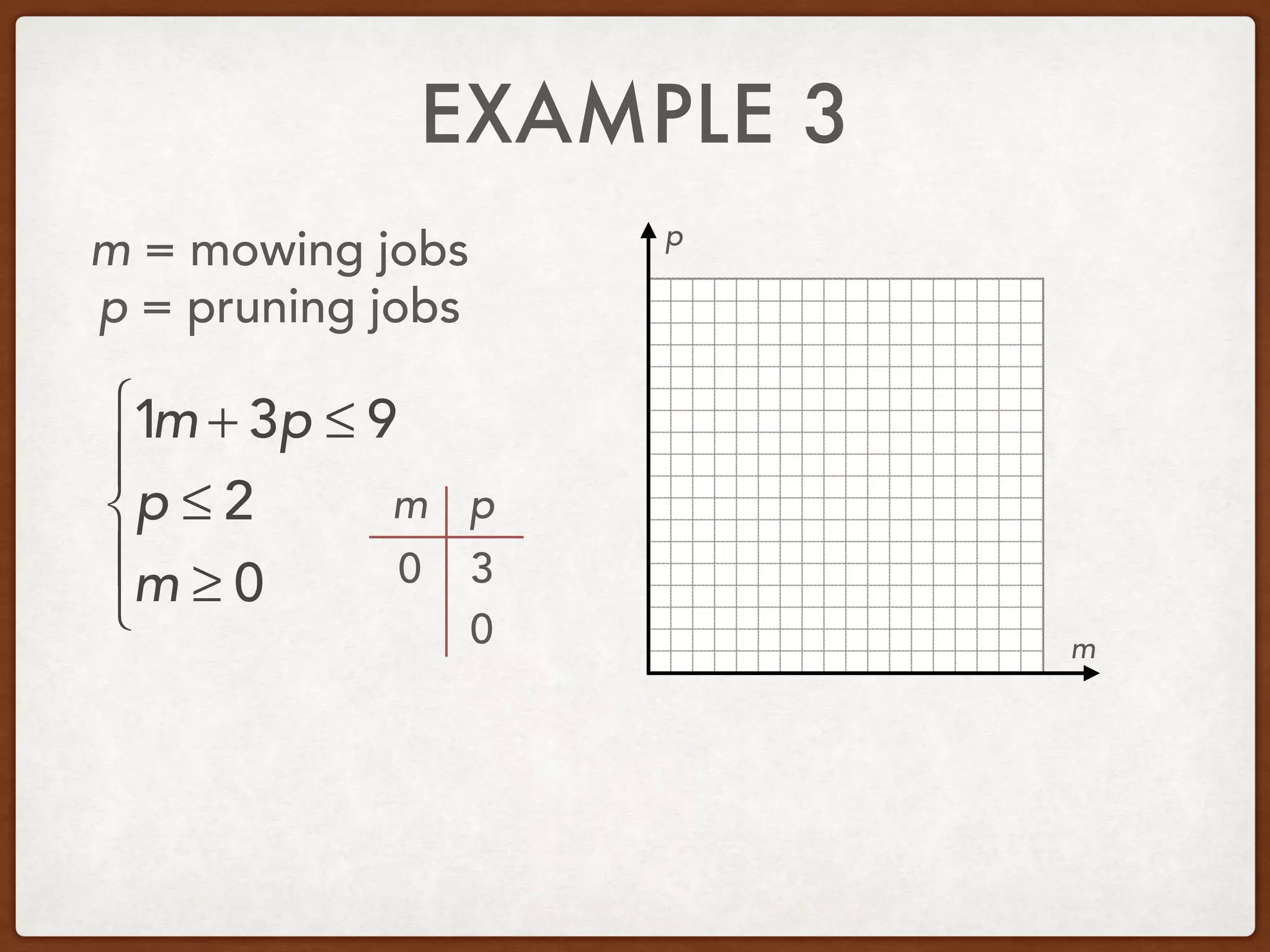
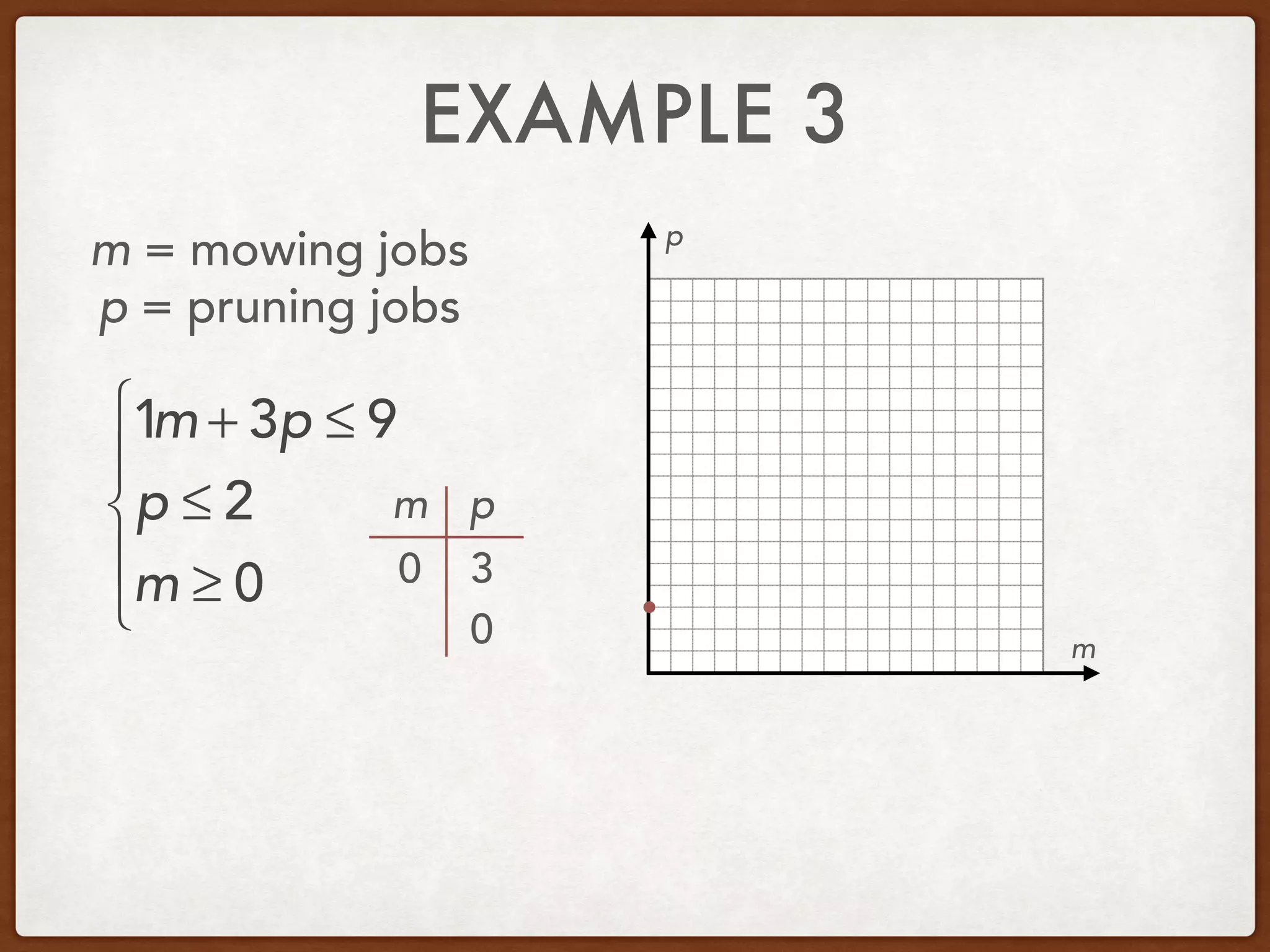
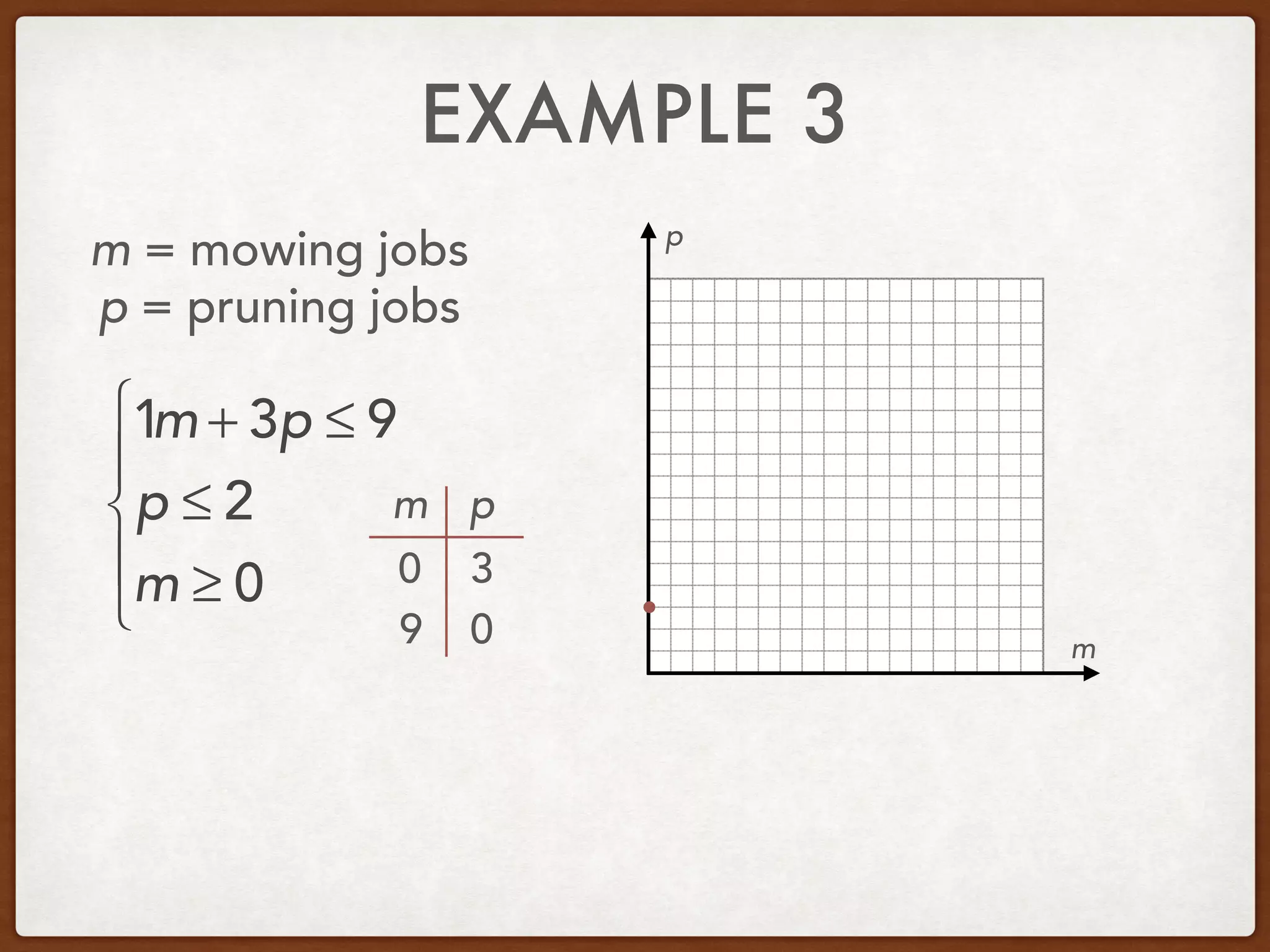
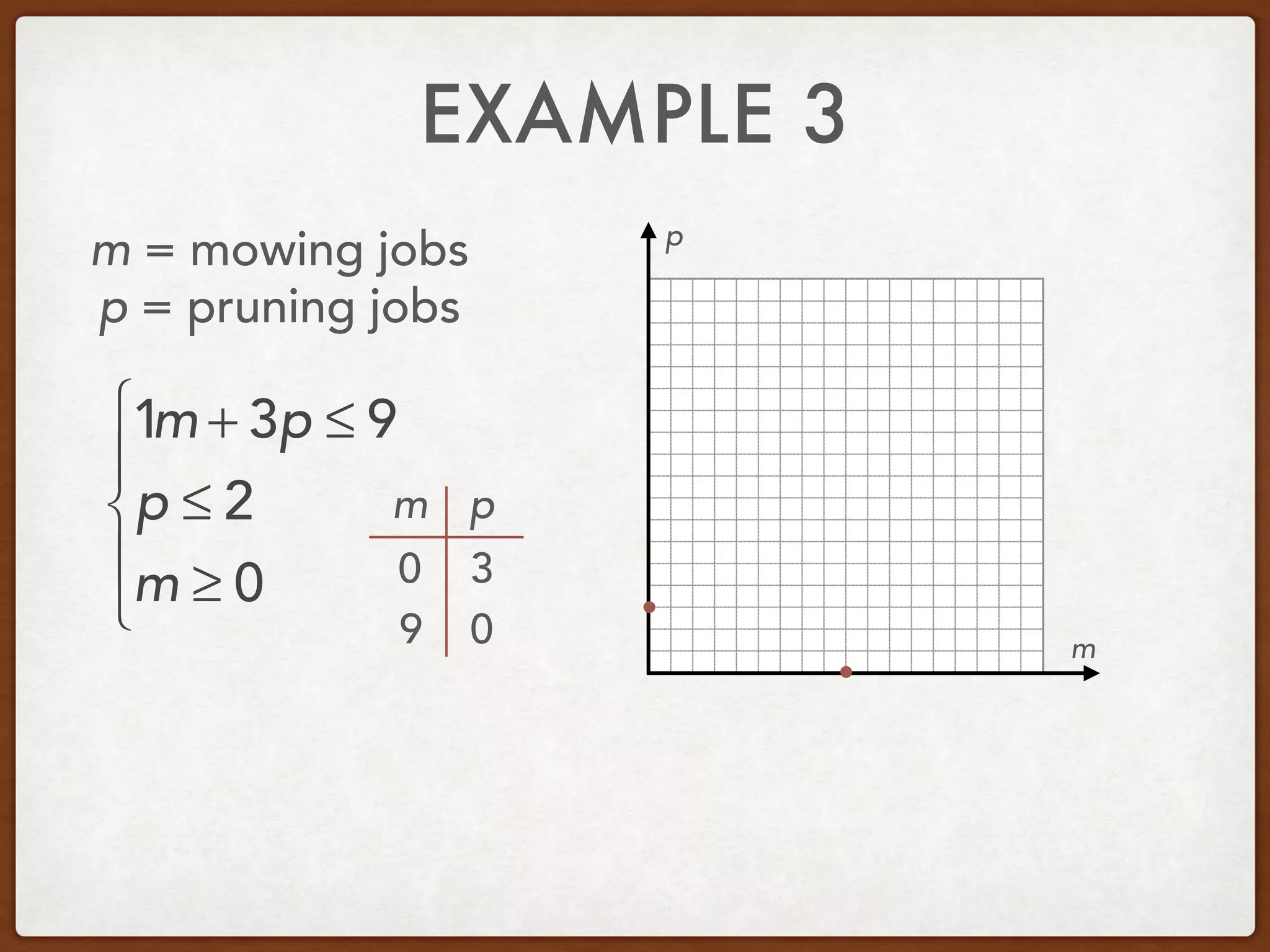
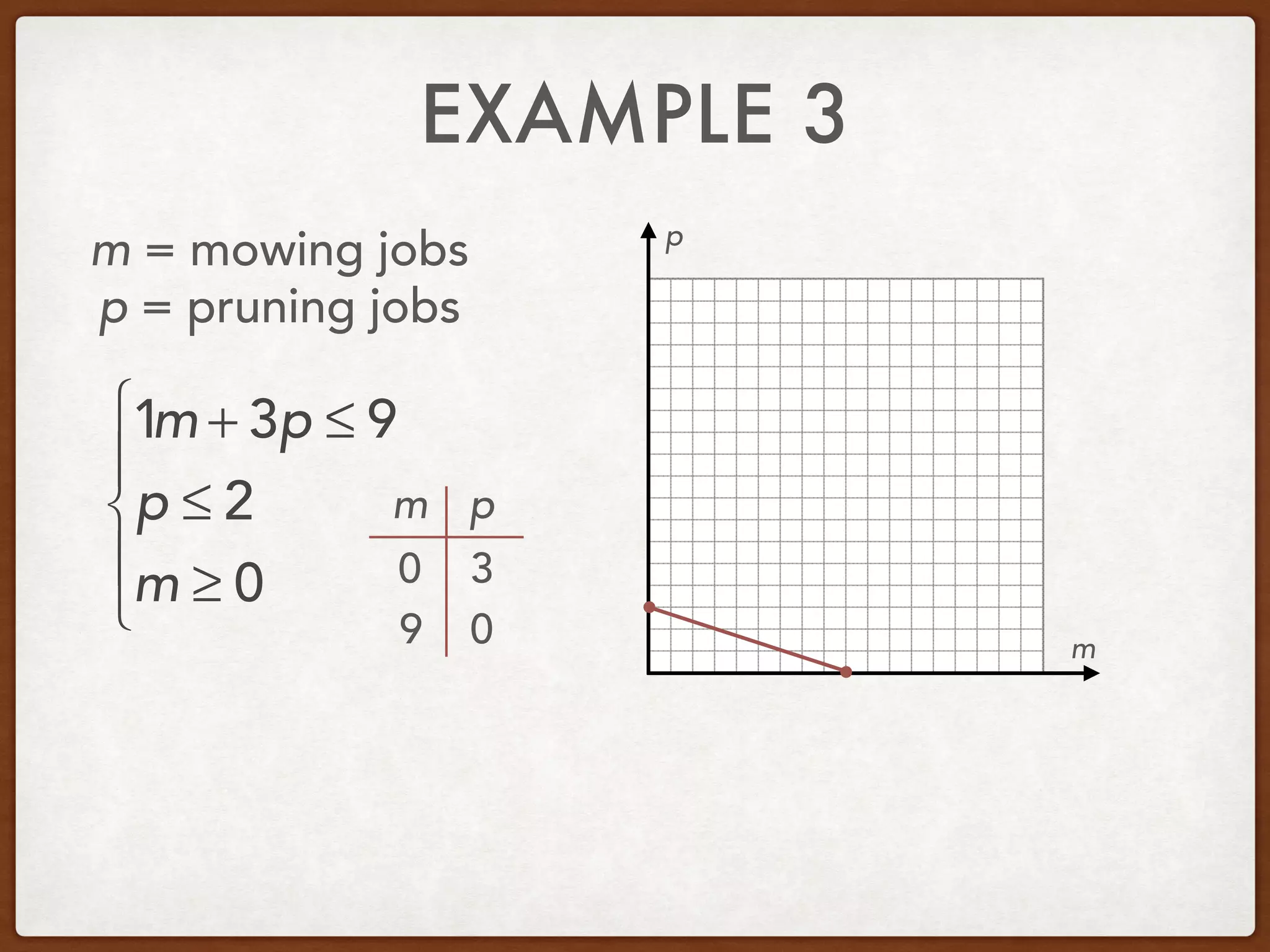
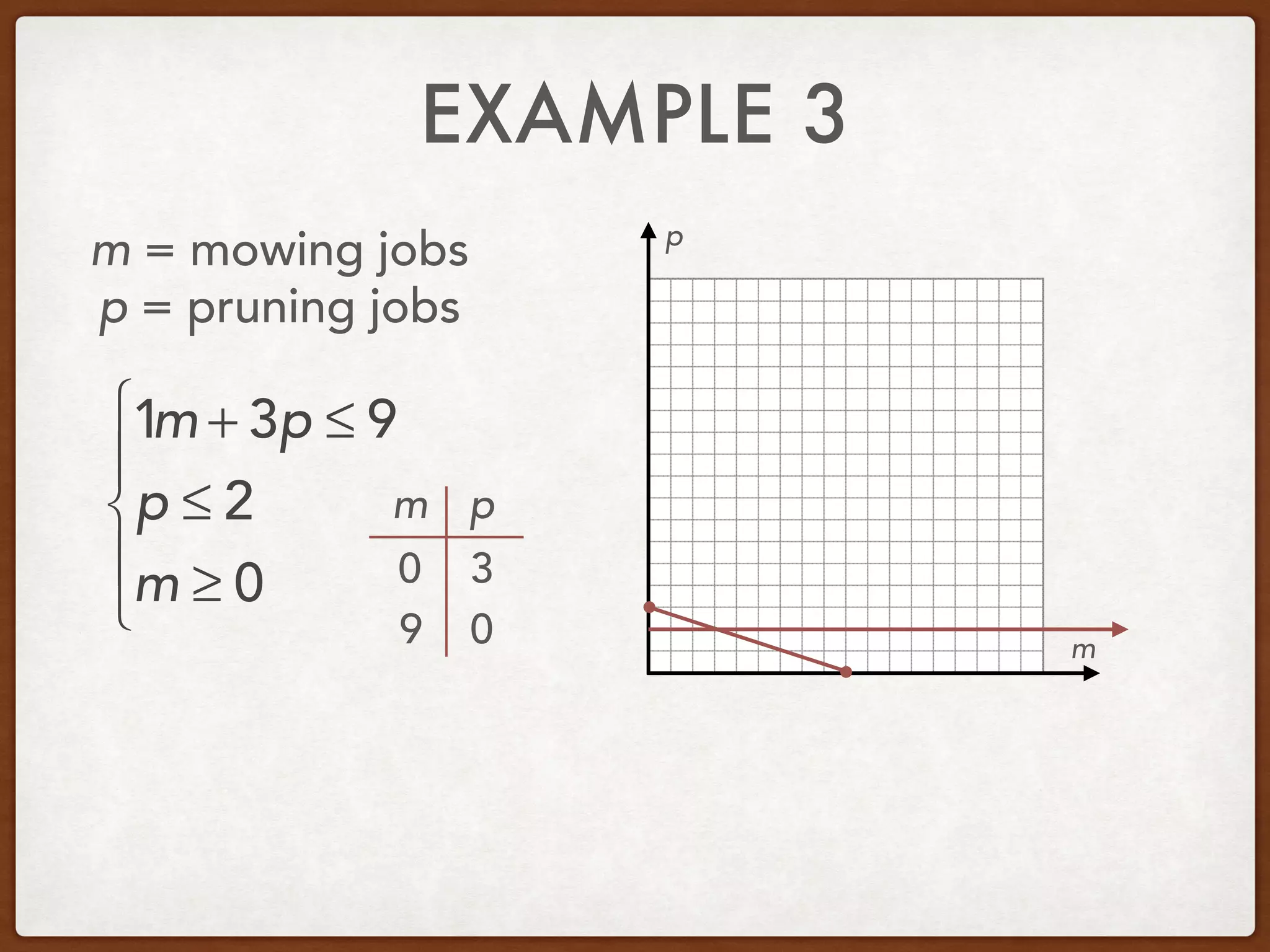
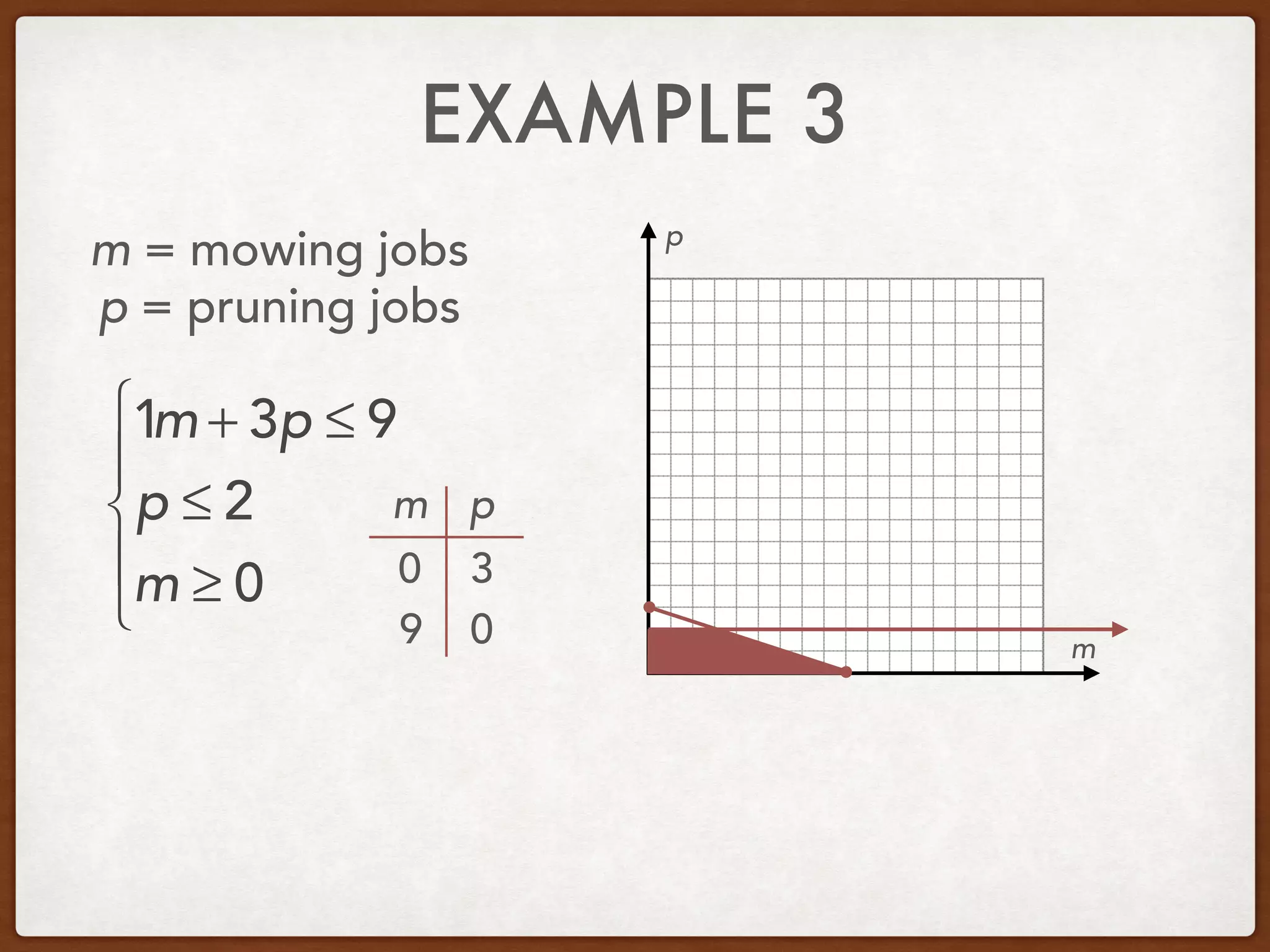
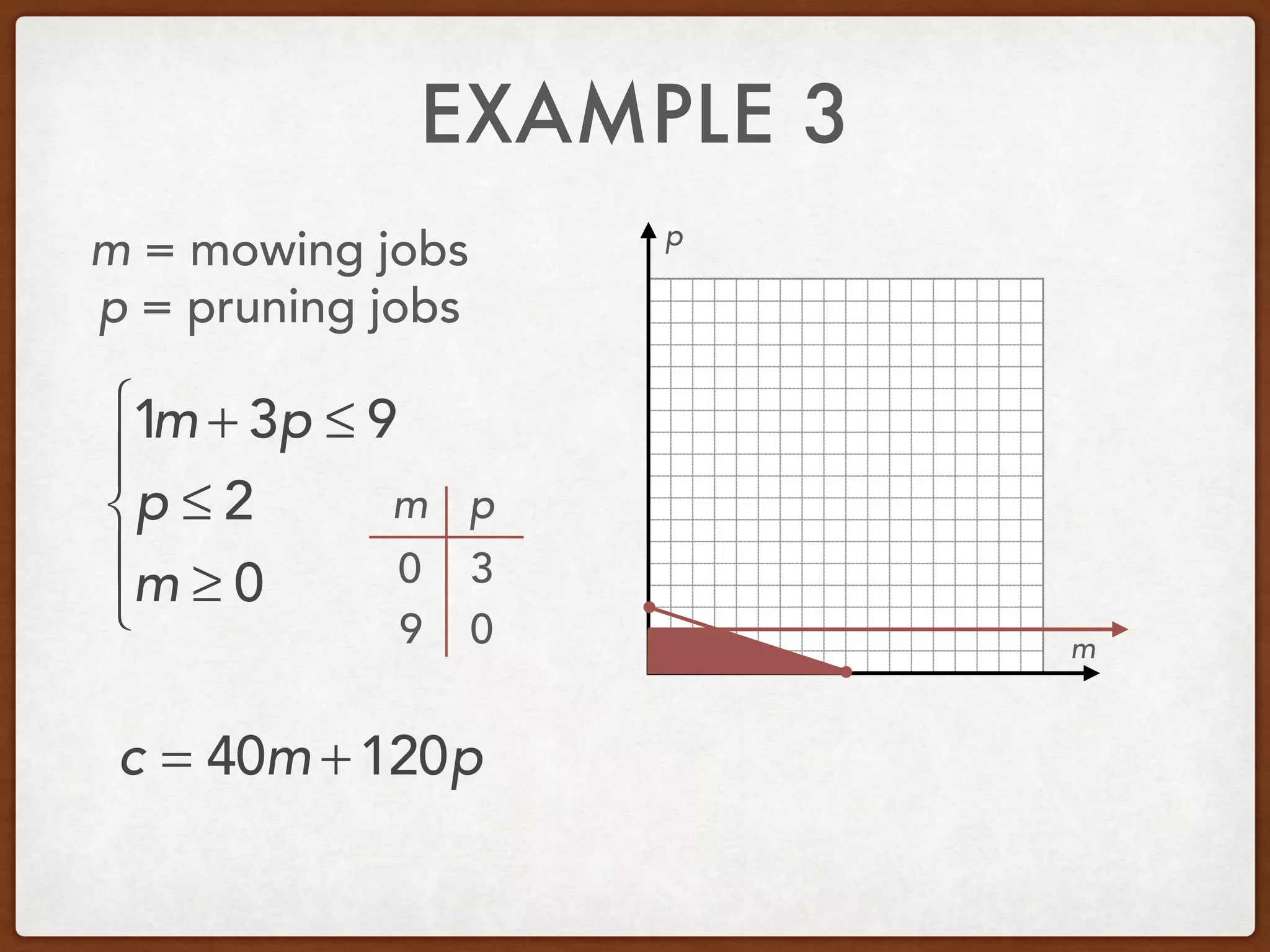
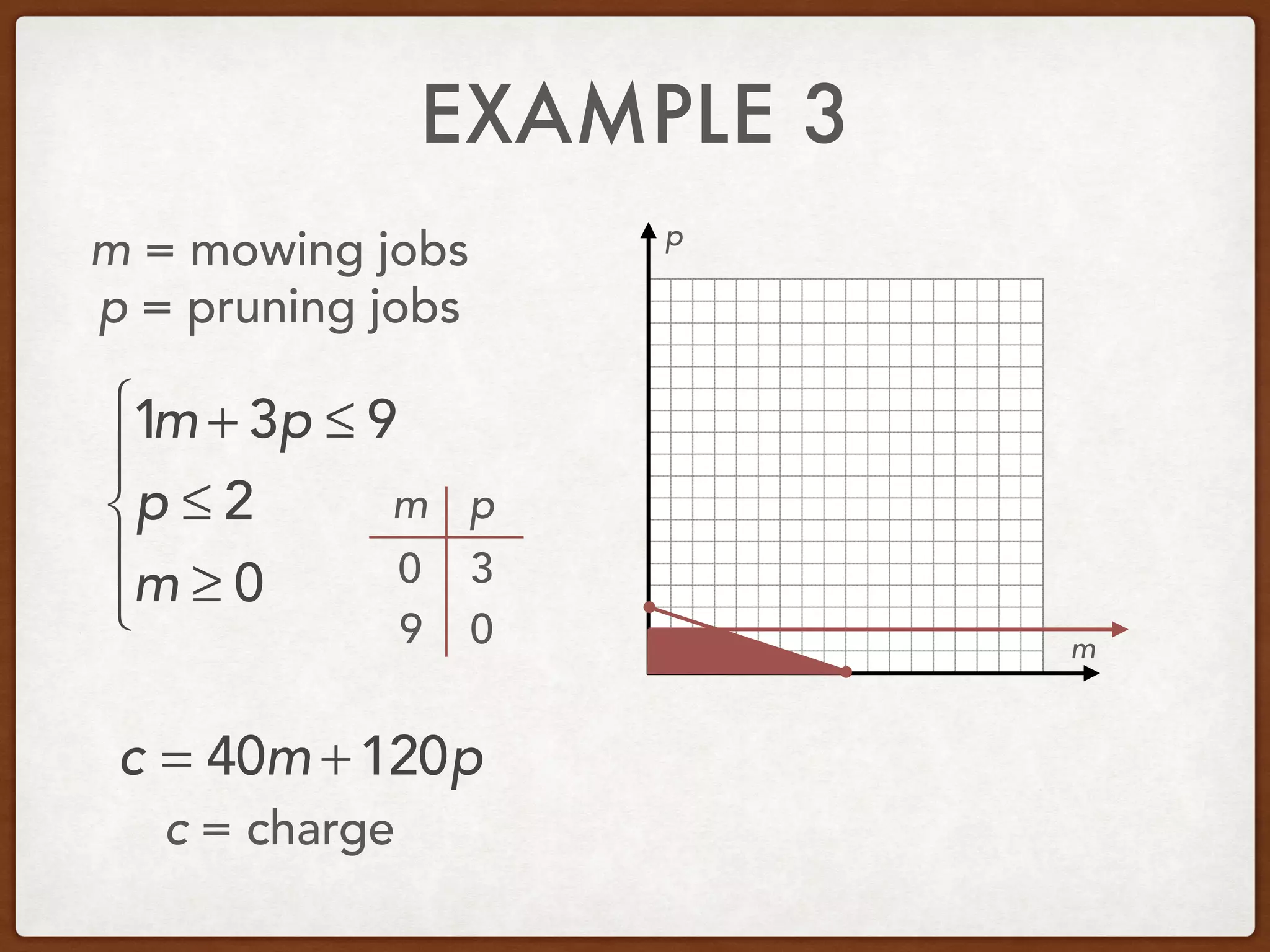
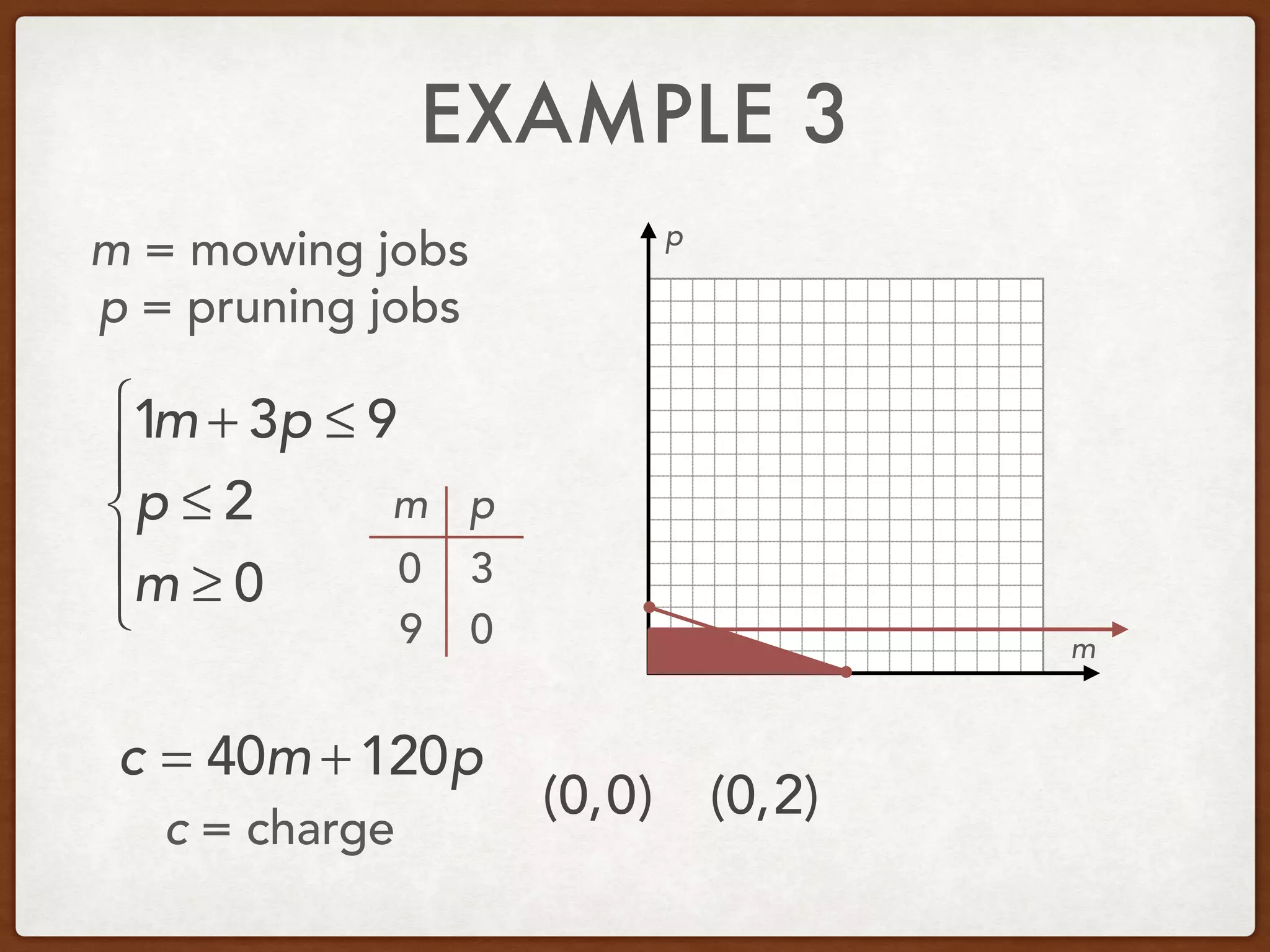
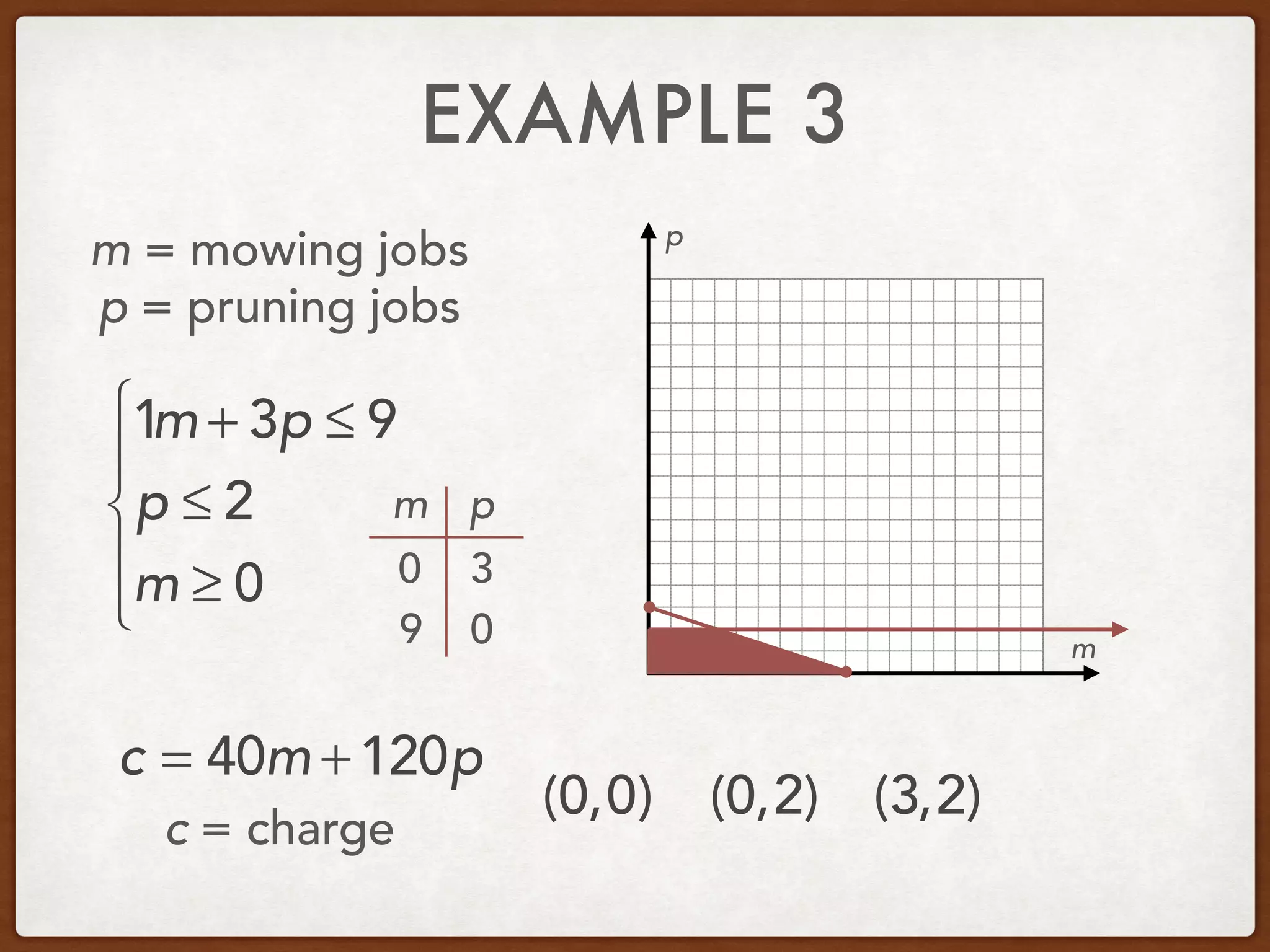
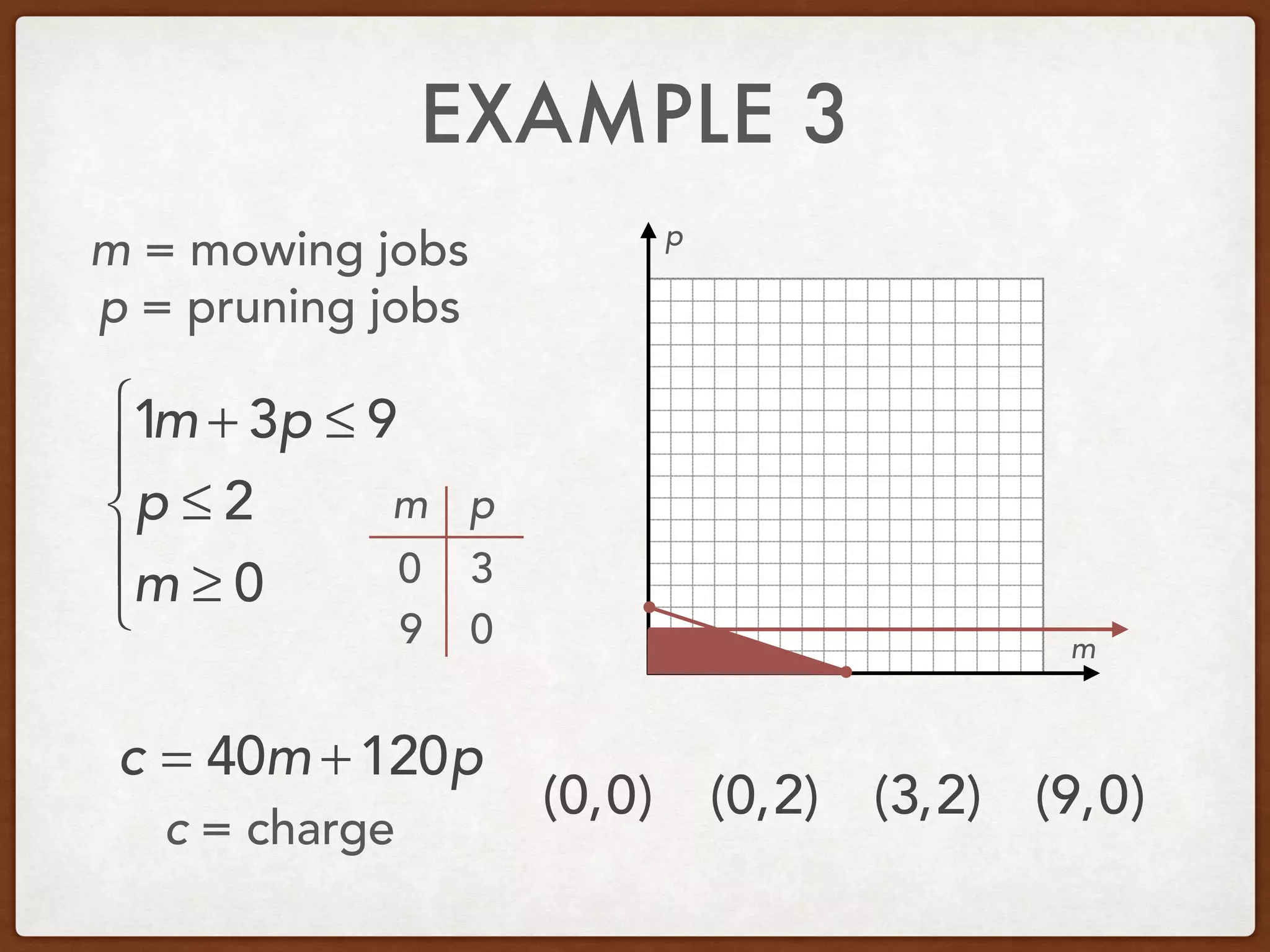
This document discusses linear programming and optimization. It begins with essential questions about finding maximum and minimum values of functions over regions. Key vocabulary is defined, including linear programming, feasible region, bounded, unbounded, and optimize. Two examples are provided to demonstrate how to graph inequality systems, identify feasible regions, and find the maximum and minimum values of an objective function over those regions using linear programming techniques.

Embed presentation

Download as PDF, PPTX
OPTIMIZATION WITH LINEAR PROGRAMMING SECTION 1-8
ESSENTIAL QUESTIONS • How do you find the maximum and minimum values of a function over a region? • How do you solve real-world optimization problems using linear programming?
VOCABULARY 1. Linear Programming: 2. Feasible Region:
VOCABULARY 1. Linear Programming: 2. Feasible Region: The method of finding the maximum or minimum values of a function over a set of linear inequalities
VOCABULARY 1. Linear Programming: 2. Feasible Region: The method of finding the maximum or minimum values of a function over a set of linear inequalities The shaded area that results as the solution to the system of inequalities
VOCABULARY 3. Bounded: 4. Unbounded: 5. Optimize:
VOCABULARY 3. Bounded: 4. Unbounded: 5. Optimize: When the feasible set is enclosed within the constraints of the system
VOCABULARY 3. Bounded: 4. Unbounded: 5. Optimize: When the feasible set is enclosed within the constraints of the system When the feasible set is open and continues on forever
VOCABULARY 3. Bounded: 4. Unbounded: 5. Optimize: When the feasible set is enclosed within the constraints of the system When the feasible set is open and continues on forever Finding the best price or amount to minimize costs or maximize profits
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ f(x,y) = 3x − 2y
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,4) f(x,y) = 3x − 2y x y 0 0 2 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,4) (5,4) f(x,y) = 3x − 2y x y 0 0 2 2
EXAMPLE 1 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y x y 0 0 2 2
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4)
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4)
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3)
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3) f(5,−3) = 15 + 6
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3) f(5,−3) = 15 + 6 f(5,4) = 21
EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3) f(5,−3) = 15 + 6 f(5,4) = 21 The maximum of 21 is at (5, -3) and the minimum of -14 is at (-2, 4).
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ f(x,y) = 2x − 3y
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,0) f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
EXAMPLE 2 Graph the system of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,0) (0,−2) f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0)
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2)
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 (0,0)Check:
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 f(0,0) = 2(0) + 3(0) (0,0)Check:
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 f(0,0) = 2(0) + 3(0) f(0,0) = 0 − 0 (0,0)Check:
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 f(0,0) = 2(0) + 3(0) f(0,0) = 0 − 0 f(0,0) = 0 (0,0)Check:
EXAMPLE 2 (−2,0) (0,−2) f(x,y) = 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 The minimum of -6 is at (0, -2) and there is no maximum. f(0,0) = 2(0) + 3(0) f(0,0) = 0 − 0 f(0,0) = 0 (0,0)Check:
EXAMPLE 3 Shecky’s Sod and Shrubs has crews that mow lawns and prune shrubbery. The company schedules one hour for mowing jobs and three hours for pruning jobs. Each crew is scheduled for no more than two pruning jobs per day. Each crew’s schedule is set up for a maximum of nine hours per day. On average, the charge for mowing a lawn is $40, and the charge for pruning shrubbery is $120. Find a combination of mowing lawns and pruning shrubs that will maximize the income the company receives per day for one of its crews.
EXAMPLE 3
EXAMPLE 3 m = mowing jobs
EXAMPLE 3 m = mowing jobs p = pruning jobs
EXAMPLE 3 m = mowing jobs p = pruning jobs ⎧ ⎨ ⎪ ⎩ ⎪
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9⎧ ⎨ ⎪ ⎩ ⎪
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 ⎧ ⎨ ⎪ ⎩ ⎪
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0)
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0) (0,2)
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0) (0,2) (3,2)
EXAMPLE 3 m = mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0) (0,2) (3,2) (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) c = $240 (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 c = 40(9) +120(0) (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 c = 40(9) +120(0) c = $360 (9,0)
EXAMPLE 3 (0,2) (3,2) c = 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 The company can make a maximum income of $360 when they either have 9 mowing jobs and 0 pruning jobs or 3 mowing jobs and 2 pruning jobs. c = 40(9) +120(0) c = $360 (9,0)

More Related Content

PPT
Solving Systems - Elimination NOTES
byswartzje
 
PDF
Algebra 2 Section 1-6
byJimbo Lamb
 
PDF
Algebra 2 Section 1-7
byJimbo Lamb
 
PDF
Algebra 2 Section 1-9
byJimbo Lamb
 
PDF
Chapter 6 taylor and maclaurin series
byIrfaan Bahadoor
 
PPT
Linear systems with 3 unknows
bymstf mstf
 
PPTX
4 3 solving linear systems by elimination
byhisema01
 
PPT
Lca10 0505
byVenkata RamBabu
 
Solving Systems - Elimination NOTES
byswartzje
 
Algebra 2 Section 1-6
byJimbo Lamb
 
Algebra 2 Section 1-7
byJimbo Lamb
 
Algebra 2 Section 1-9
byJimbo Lamb
 
Chapter 6 taylor and maclaurin series
byIrfaan Bahadoor
 
Linear systems with 3 unknows
bymstf mstf
 
4 3 solving linear systems by elimination
byhisema01
 
Lca10 0505
byVenkata RamBabu
 

What's hot

PDF
Unit2 vrs
byAkhilesh Deshpande
 
PDF
11 X1 T01 08 Simultaneous Equations (2010)
byNigel Simmons
 
PPT
Systems Non Linear Equations
byBitsy Griffin
 
PPT
Elimination method Ch 7
byWood-Ridge
 
KEY
0908 ch 9 day 8
byfestivalelmo
 
PPTX
Simultaneous equations (2)
byArjuna Senanayake
 
PDF
Unit1 vrs
byAkhilesh Deshpande
 
PPTX
3 2 solving systems of equations (elimination method)
byHazel Joy Chong
 
PDF
Substitution Method of Systems of Linear Equations
bySonarin Cruz
 
PPT
Solving Systems by Substitution
byswartzje
 
PPT
Simultaneous equations
bysuefee
 
DOCX
.Chapter7&8.
byjennytuazon01630
 
PPTX
Higherorder non homogeneous partial differrential equations (Maths 3) Power P...
byvrajes
 
PDF
Elimination of Systems of Linear Equation
bySonarin Cruz
 
PPTX
January18
bykhyps13
 
PPT
Ca mod06 les01
byRobert Hill
 
PDF
Graphical Solution of Systems of Linear Equations
bySonarin Cruz
 
PPT
Systems of linear equations
bygandhinagar
 
PPTX
Alg2 lesson 3-2
byCarol Defreese
 
PPTX
15.2 solving systems of equations by substitution
byGlenSchlee
 
Unit2 vrs
byAkhilesh Deshpande
 
11 X1 T01 08 Simultaneous Equations (2010)
byNigel Simmons
 
Systems Non Linear Equations
byBitsy Griffin
 
Elimination method Ch 7
byWood-Ridge
 
0908 ch 9 day 8
byfestivalelmo
 
Simultaneous equations (2)
byArjuna Senanayake
 
Unit1 vrs
byAkhilesh Deshpande
 
3 2 solving systems of equations (elimination method)
byHazel Joy Chong
 
Substitution Method of Systems of Linear Equations
bySonarin Cruz
 
Solving Systems by Substitution
byswartzje
 
Simultaneous equations
bysuefee
 
.Chapter7&8.
byjennytuazon01630
 
Higherorder non homogeneous partial differrential equations (Maths 3) Power P...
byvrajes
 
Elimination of Systems of Linear Equation
bySonarin Cruz
 
January18
bykhyps13
 
Ca mod06 les01
byRobert Hill
 
Graphical Solution of Systems of Linear Equations
bySonarin Cruz
 
Systems of linear equations
bygandhinagar
 
Alg2 lesson 3-2
byCarol Defreese
 
15.2 solving systems of equations by substitution
byGlenSchlee
 

Similar to Algebra 2 Section 1-8

PDF
Lecture 7.1 to 7.2 bt
bybtmathematics
 
PDF
Introduction to Linear Programming-2.pdf
bylioneljchacha
 
PPTX
Lecture 7.2 bt
bybtmathematics
 
PPTX
System of linear inequalities
bymstf mstf
 
PPTX
Chapter 4 review
bygregcross22
 
PPTX
Alg II Unit 3-4-linear programingintro
byjtentinger
 
PPTX
Optimization Techniques : A subject of 4th sem engineering
byNamJ1
 
PPTX
Quadratic Functions graph
byRefat Ullah
 
PPT
3.4 a linear programming
byfthrower
 
PPT
LP2As the EEM of Engineering Department of Taxila.ppt
byWAQASASHIQ6
 
PDF
9.6 Systems of Inequalities and Linear Programming
bysmiller5
 
PPTX
OT-PPT Optimization Techniques in chemical process.pptx
byiushuaibu
 
PPT
Linear Programming Mathematics in the Modern World
bylunawasabilune
 
PPT
A geometrical approach in Linear Programming Problems
byRaja Agrawal
 
PPT
3.4 linear programming
byfthrower
 
PPT
Solving linear inequalities in one variable
bychetnasingh1804
 
PPTX
Chap3 (1) Introduction to Management Sciences
bySyed Shahzad Ali
 
KEY
Integrated Math 2 Section 8-7
byJimbo Lamb
 
PDF
Algebra 2 Section 5-2
byJimbo Lamb
 
PDF
Sample2
byNima Rasekh
 
Lecture 7.1 to 7.2 bt
bybtmathematics
 
Introduction to Linear Programming-2.pdf
bylioneljchacha
 
Lecture 7.2 bt
bybtmathematics
 
System of linear inequalities
bymstf mstf
 
Chapter 4 review
bygregcross22
 
Alg II Unit 3-4-linear programingintro
byjtentinger
 
Optimization Techniques : A subject of 4th sem engineering
byNamJ1
 
Quadratic Functions graph
byRefat Ullah
 
3.4 a linear programming
byfthrower
 
LP2As the EEM of Engineering Department of Taxila.ppt
byWAQASASHIQ6
 
9.6 Systems of Inequalities and Linear Programming
bysmiller5
 
OT-PPT Optimization Techniques in chemical process.pptx
byiushuaibu
 
Linear Programming Mathematics in the Modern World
bylunawasabilune
 
A geometrical approach in Linear Programming Problems
byRaja Agrawal
 
3.4 linear programming
byfthrower
 
Solving linear inequalities in one variable
bychetnasingh1804
 
Chap3 (1) Introduction to Management Sciences
bySyed Shahzad Ali
 
Integrated Math 2 Section 8-7
byJimbo Lamb
 
Algebra 2 Section 5-2
byJimbo Lamb
 
Sample2
byNima Rasekh
 

More from Jimbo Lamb

PDF
Geometry Section 1-5
byJimbo Lamb
 
PDF
Geometry Section 1-4
byJimbo Lamb
 
PDF
Geometry Section 1-3
byJimbo Lamb
 
PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-1
byJimbo Lamb
 
PDF
Algebra 2 Section 5-3
byJimbo Lamb
 
PDF
Algebra 2 Section 5-1
byJimbo Lamb
 
PDF
Algebra 2 Section 4-9
byJimbo Lamb
 
PDF
Algebra 2 Section 4-8
byJimbo Lamb
 
PDF
Algebra 2 Section 4-6
byJimbo Lamb
 
PDF
Geometry Section 6-6
byJimbo Lamb
 
PDF
Geometry Section 6-5
byJimbo Lamb
 
PDF
Geometry Section 6-4
byJimbo Lamb
 
PDF
Geometry Section 6-3
byJimbo Lamb
 
PDF
Geometry Section 6-2
byJimbo Lamb
 
PDF
Geometry Section 6-1
byJimbo Lamb
 
PDF
Algebra 2 Section 4-5
byJimbo Lamb
 
PDF
Algebra 2 Section 4-4
byJimbo Lamb
 
PDF
Algebra 2 Section 4-2
byJimbo Lamb
 
Geometry Section 1-5
byJimbo Lamb
 
Geometry Section 1-4
byJimbo Lamb
 
Geometry Section 1-3
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-1
byJimbo Lamb
 
Algebra 2 Section 5-3
byJimbo Lamb
 
Algebra 2 Section 5-1
byJimbo Lamb
 
Algebra 2 Section 4-9
byJimbo Lamb
 
Algebra 2 Section 4-8
byJimbo Lamb
 
Algebra 2 Section 4-6
byJimbo Lamb
 
Geometry Section 6-6
byJimbo Lamb
 
Geometry Section 6-5
byJimbo Lamb
 
Geometry Section 6-4
byJimbo Lamb
 
Geometry Section 6-3
byJimbo Lamb
 
Geometry Section 6-2
byJimbo Lamb
 
Geometry Section 6-1
byJimbo Lamb
 
Algebra 2 Section 4-5
byJimbo Lamb
 
Algebra 2 Section 4-4
byJimbo Lamb
 
Algebra 2 Section 4-2
byJimbo Lamb
 

Recently uploaded

PPTX
How to Automate Quality Checks in Odoo 18 Quality App
byCeline George
 
PPTX
Parts of speech Nouns, Pronouns, Verbs, Adverbs etc.pptx
byFarhan Amjad Gondal
 
PDF
2025 | Quiz9 | Cinema Connect Trivia Questions Only
bySoumik Biswas
 
PPTX
CROP RESIDUE MANAGEMANT AND ITS EFFECT ON SOIL HEALTH
byShraddha Maurya
 
PPTX
Role of the Uninstall Hook in Odoo 18 Module Cleanup
byCeline George
 
PDF
Handwritten notes of Toxicity 1. Genotoxicity 2 Carcinogenicity 3 Teratogenic...
byjagdeepsinghynr7
 
PPTX
Summary for systematic review - Adrine Nyamwiza
bySystematic Reviews Network (SRN)
 
PDF
Prescription Writing- Elements, Parts, and Exercises
byDr. Ishita Agarwal
 
PDF
Orchard Floor Managment.pdf Orchard Floor Management
bybisensharad
 
PDF
Basics of Systematic Literature Search - Nasra Gathoni
bySystematic Reviews Network (SRN)
 
PDF
FAMILY ASSESSMENT FORMAT - CHN practical
byDr. Sudhadevi Sadanandan
 
PDF
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
PDF
Ketogenic diet in Epilepsy in children..
bymirzasania0810
 
PDF
Nutrients & Role in Horticulture.pdf, Dr. Sharad Bisen Horticulture
bybisensharad
 
PDF
Chaplin's Visual Critique of Modernism: Modern Times and The Great Dictator
bykrutivyas2005
 
PDF
Language and curriculum (B. Ed) semester 2
bynehapanna60
 
PDF
The Drift Principle: When Information Accelerates Faster Than Minds Can Compress
byReality Drift Archive
 
PPTX
Details of Muscular-and-Nervous-Tissues.pptx
byAshish Umale
 
PPTX
AsiaSweep 2025 Questions Only--FINAL .ppt
byArul Mani
 
DOCX
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 
How to Automate Quality Checks in Odoo 18 Quality App
byCeline George
 
Parts of speech Nouns, Pronouns, Verbs, Adverbs etc.pptx
byFarhan Amjad Gondal
 
2025 | Quiz9 | Cinema Connect Trivia Questions Only
bySoumik Biswas
 
CROP RESIDUE MANAGEMANT AND ITS EFFECT ON SOIL HEALTH
byShraddha Maurya
 
Role of the Uninstall Hook in Odoo 18 Module Cleanup
byCeline George
 
Handwritten notes of Toxicity 1. Genotoxicity 2 Carcinogenicity 3 Teratogenic...
byjagdeepsinghynr7
 
Summary for systematic review - Adrine Nyamwiza
bySystematic Reviews Network (SRN)
 
Prescription Writing- Elements, Parts, and Exercises
byDr. Ishita Agarwal
 
Orchard Floor Managment.pdf Orchard Floor Management
bybisensharad
 
Basics of Systematic Literature Search - Nasra Gathoni
bySystematic Reviews Network (SRN)
 
FAMILY ASSESSMENT FORMAT - CHN practical
byDr. Sudhadevi Sadanandan
 
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
Ketogenic diet in Epilepsy in children..
bymirzasania0810
 
Nutrients & Role in Horticulture.pdf, Dr. Sharad Bisen Horticulture
bybisensharad
 
Chaplin's Visual Critique of Modernism: Modern Times and The Great Dictator
bykrutivyas2005
 
Language and curriculum (B. Ed) semester 2
bynehapanna60
 
The Drift Principle: When Information Accelerates Faster Than Minds Can Compress
byReality Drift Archive
 
Details of Muscular-and-Nervous-Tissues.pptx
byAshish Umale
 
AsiaSweep 2025 Questions Only--FINAL .ppt
byArul Mani
 
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 

Algebra 2 Section 1-8

  • 1.
  • 2.
    ESSENTIAL QUESTIONS • Howdo you find the maximum and minimum values of a function over a region? • How do you solve real-world optimization problems using linear programming?
  • 3.
  • 4.
    VOCABULARY 1. Linear Programming: 2.Feasible Region: The method of finding the maximum or minimum values of a function over a set of linear inequalities
  • 5.
    VOCABULARY 1. Linear Programming: 2.Feasible Region: The method of finding the maximum or minimum values of a function over a set of linear inequalities The shaded area that results as the solution to the system of inequalities
  • 6.
  • 7.
    VOCABULARY 3. Bounded: 4. Unbounded: 5.Optimize: When the feasible set is enclosed within the constraints of the system
  • 8.
    VOCABULARY 3. Bounded: 4. Unbounded: 5.Optimize: When the feasible set is enclosed within the constraints of the system When the feasible set is open and continues on forever
  • 9.
    VOCABULARY 3. Bounded: 4. Unbounded: 5.Optimize: When the feasible set is enclosed within the constraints of the system When the feasible set is open and continues on forever Finding the best price or amount to minimize costs or maximize profits
  • 10.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ f(x,y) = 3x − 2y
  • 11.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y
  • 12.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y
  • 13.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y
  • 14.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0
  • 15.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2
  • 16.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2
  • 17.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
  • 18.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
  • 19.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
  • 20.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 3x − 2y x y 0 0 2 2
  • 21.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,4) f(x,y) = 3x − 2y x y 0 0 2 2
  • 22.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,4) (5,4) f(x,y) = 3x − 2y x y 0 0 2 2
  • 23.
    EXAMPLE 1 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. x ≤ 5 y ≤ 4 x + y ≥ 2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,4) (5,4) (5,−3) f(x,y) = 3x − 2y x y 0 0 2 2
  • 24.
  • 25.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4)
  • 26.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8
  • 27.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14
  • 28.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4)
  • 29.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8
  • 30.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7
  • 31.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3)
  • 32.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3) f(5,−3) = 15 + 6
  • 33.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3) f(5,−3) = 15 + 6 f(5,4) = 21
  • 34.
    EXAMPLE 1 (−2,4) (5,4) (5,−3) f(x,y)= 3x − 2y f(−2,4) = 3(−2) − 2(4) f(−2,4) = −6 − 8 f(−2,4) = −14 f(5,4) = 3(5) − 2(4) f(5,4) = 15 − 8 f(5,4) = 7 f(5,−3) = 3(5) − 2(−3) f(5,−3) = 15 + 6 f(5,4) = 21 The maximum of 21 is at (5, -3) and the minimum of -14 is at (-2, 4).
  • 35.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ f(x,y) = 2x − 3y
  • 36.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y
  • 37.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0
  • 38.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1
  • 39.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1
  • 40.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2
  • 41.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2
  • 42.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2
  • 43.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0
  • 44.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2
  • 45.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2
  • 46.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4
  • 47.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4
  • 48.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4
  • 49.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0
  • 50.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2
  • 51.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
  • 52.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
  • 53.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
  • 54.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,0) f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
  • 55.
    EXAMPLE 2 Graph thesystem of inequalities. Name the coordinates of the feasible region. Find the maximum and minimum values of the function provided for this region. −x + 2y ≤ 2 x − 2y ≤ 4 x + y ≥ −2 ⎧ ⎨ ⎪ ⎩ ⎪ x y (−2,0) (0,−2) f(x,y) = 2x − 3y x y 0 0 1 -2 x y 0 0 -2 4 x y 0 0 -2 -2
  • 56.
  • 57.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0)
  • 58.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0
  • 59.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4
  • 60.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2)
  • 61.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6
  • 62.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6
  • 63.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 (0,0)Check:
  • 64.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 f(0,0) = 2(0) + 3(0) (0,0)Check:
  • 65.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 f(0,0) = 2(0) + 3(0) f(0,0) = 0 − 0 (0,0)Check:
  • 66.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 f(0,0) = 2(0) + 3(0) f(0,0) = 0 − 0 f(0,0) = 0 (0,0)Check:
  • 67.
    EXAMPLE 2 (−2,0) (0,−2) f(x,y)= 2x + 3y f(−2,0) = 2(−2) + 3(0) f(−2,0) = −4 + 0 f(−2,0) = −4 f(0,−2) = 2(0) + 3(−2) f(0,−2) = 0 − 6 f(0,−2) = −6 The minimum of -6 is at (0, -2) and there is no maximum. f(0,0) = 2(0) + 3(0) f(0,0) = 0 − 0 f(0,0) = 0 (0,0)Check:
  • 68.
    EXAMPLE 3 Shecky’s Sodand Shrubs has crews that mow lawns and prune shrubbery. The company schedules one hour for mowing jobs and three hours for pruning jobs. Each crew is scheduled for no more than two pruning jobs per day. Each crew’s schedule is set up for a maximum of nine hours per day. On average, the charge for mowing a lawn is $40, and the charge for pruning shrubbery is $120. Find a combination of mowing lawns and pruning shrubs that will maximize the income the company receives per day for one of its crews.
  • 69.
  • 70.
    EXAMPLE 3 m =mowing jobs
  • 71.
    EXAMPLE 3 m =mowing jobs p = pruning jobs
  • 72.
    EXAMPLE 3 m =mowing jobs p = pruning jobs ⎧ ⎨ ⎪ ⎩ ⎪
  • 73.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9⎧ ⎨ ⎪ ⎩ ⎪
  • 74.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 ⎧ ⎨ ⎪ ⎩ ⎪
  • 75.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪
  • 76.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p
  • 77.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0
  • 78.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3
  • 79.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3
  • 80.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
  • 81.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
  • 82.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
  • 83.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
  • 84.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9
  • 85.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p
  • 86.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge
  • 87.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0)
  • 88.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0) (0,2)
  • 89.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0) (0,2) (3,2)
  • 90.
    EXAMPLE 3 m =mowing jobs p = pruning jobs 1m + 3p ≤ 9 p ≤ 2 m ≥ 0 ⎧ ⎨ ⎪ ⎩ ⎪ m p m p 0 0 3 9 c = 40m +120p c = charge (0,0) (0,2) (3,2) (9,0)
  • 91.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p (9,0)
  • 92.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) (9,0)
  • 93.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) c = $240 (9,0)
  • 94.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) (9,0)
  • 95.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 (9,0)
  • 96.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 (9,0)
  • 97.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 c = 40(9) +120(0) (9,0)
  • 98.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 c = 40(9) +120(0) c = $360 (9,0)
  • 99.
    EXAMPLE 3 (0,2) (3,2) c= 40m +120p c = 40(0) +120(2) c = $240 c = 40(3) +120(2) c = 120 + 240 c = $360 The company can make a maximum income of $360 when they either have 9 mowing jobs and 0 pruning jobs or 3 mowing jobs and 2 pruning jobs. c = 40(9) +120(0) c = $360 (9,0)