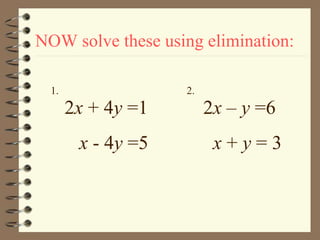The document describes the elimination method for solving systems of equations. The key steps are: 1) Write both equations in standard form Ax + By = C 2) Determine which variable to eliminate using addition or subtraction 3) Solve the resulting equation for one variable 4) Substitute back into the original equation to solve for the other variable 5) Check that the solution satisfies both original equations It provides examples showing how to set up and solve systems of equations using elimination, including word problems about supplementary angles and finding two numbers based on their sum and difference.

1. 3-2: Solving Systems of Equations
using Elimination
Steps:
1. Place both equations in Standard Form, Ax + By = C.
2. Determine which variable to eliminate with Addition
or Subtraction.
3. Solve for the variable left.
4. Go back and use the found variable in step 3 to find
second variable.
5. Check the solution in both equations of the system.

2. EXAMPLE #1:
5x + 3y = 11
5x = 2y + 1
STEP1: Write both equations in Ax + By = C
form. 5x + 3y =1
5x - 2y =1
STEP 2: Use subtraction to eliminate 5x.
5x + 3y =11 5x + 3y = 11
-(5x - 2y =1) -5x + 2y = -1
Note: the (-) is distributed.
STEP 3: Solve for the variable.
5x + 3y =11
-5x + 2y = -1
5y =10 y = 2

3. STEP 4: Solve for the other variable by substituting
into either equation.
5x + 3y =11
5x + 3(2) =11
5x + 6 =11
5x = 5
x = 1
5x + 3y = 11
5x = 2y + 1
The solution to the system is (1,2).

4. 5x + 3y= 11
5x = 2y + 1
Step 5: Check the solution in both equations.
The solution to the system is (1,2).
5x + 3y = 11
5(1) + 3(2) =11
5 + 6 =11
11=11
5x = 2y + 1
5(1) = 2(2) + 1
5 = 4 + 1
5=5

5. Solving Systems of Equations
using Elimination
Steps:
1. Place both equations in Standard Form, Ax + By = C.
2. Determine which variable to eliminate with Addition
or Subtraction.
3. Solve for the remaining variable.
4. Go back and use the variable found in step 3 to find
the second variable.
5. Check the solution in both equations of the system.

6. Example #2: x + y = 10
5x – y = 2
Step 1: The equations are already in standard
form: x + y = 10
5x – y = 2
Step 2: Adding the equations will eliminate y.
x + y = 10 x + y = 10
+(5x – y = 2) +5x – y = +2
Step 3: Solve for the variable.
x + y = 10
+5x – y = +2
6x = 12
x = 2

7. x + y = 10
5x – y = 2
Step 4: Solve for the other variable by
substituting into either equation.
x + y = 10
2 + y = 10
y = 8
Solution to the system is (2,8).

8. x + y = 10
5x – y = 2
Step 5: Check the solution in both equations.
x + y =10
2 + 8 =10
10=10
5x – y =2
5(2) - (8) =2
10 – 8 =2
2=2
Solution to the system is (2,8).

9. NOW solve these using elimination:
1. 2.
2x + 4y =1
x - 4y =5
2x – y =6
x + y = 3

10. Using Elimination to Solve a
Word Problem:
Two angles are supplementary. The
measure of one angle is 10 degrees
more than three times the other.
Find the measure of each angle.

11. Using Elimination to Solve a
Word Problem:
Two angles are supplementary. The
measure of one angle is 10 more
than three times the other. Find the
measure of each angle.
x = degree measure of angle #1
y = degree measure of angle #2
Therefore x + y = 180

12. Using Elimination to Solve a
Word Problem:
Two angles are supplementary. The
measure of one angle is 10 more
than three times the other. Find the
measure of each angle.
x + y = 180
x =10 + 3y

13. Using Elimination to Solve a
Word Problem:
Solve
x + y = 180
x =10 + 3y
x + y = 180
-(x - 3y = 10)
4y =170
y = 42.5
x + 42.5 = 180
x = 180 - 42.5
x = 137.5
(137.5, 42.5)

14. Using Elimination to Solve a
Word Problem:
The sum of two numbers is 70
and their difference is 24. Find
the two numbers.

15. Using Elimination to Solve a
Word problem:
The sum of two numbers is 70
and their difference is 24. Find
the two numbers.
x = first number
y = second number
Therefore, x + y = 70

16. Using Elimination to Solve a
Word Problem:
The sum of two numbers is 70
and their difference is 24. Find
the two numbers.
x + y = 70
x – y = 24

17. Using Elimination to Solve a
Word Problem:
x + y =70
x - y = 24
2x = 94
x = 47
47 + y = 70
y = 70 – 47
y = 23
(47, 23)

18. Now you Try to Solve These
Problems Using Elimination.
Solve
1. Find two numbers whose sum is
18 and whose difference is 22.
2. The sum of two numbers is 128
and their difference is 114. Find
the numbers.