Uploaded byMohammad Imam Hossain
AI 6 | Adversarial Search
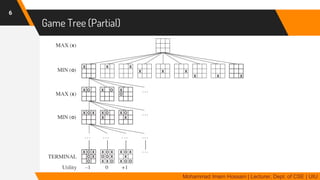
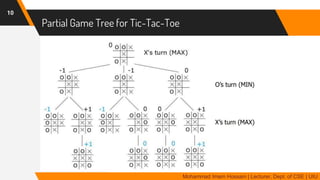
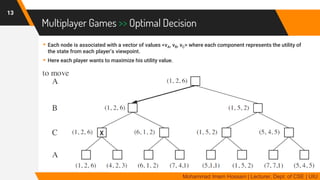
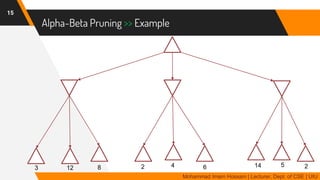
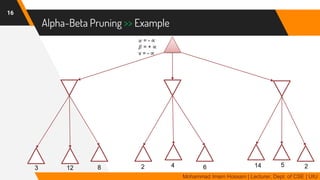
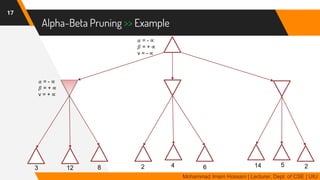
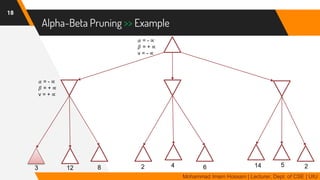
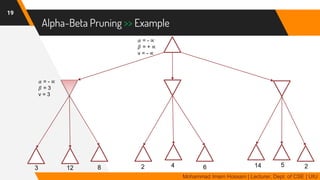
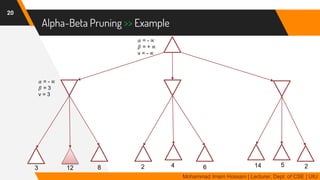
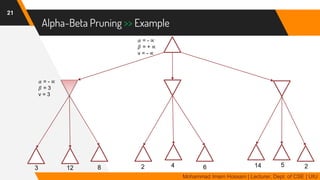
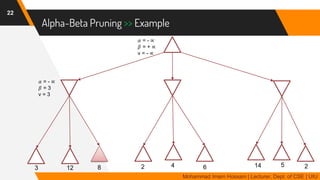
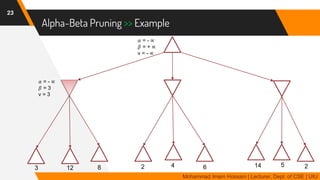
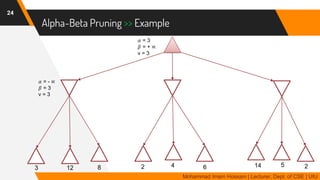
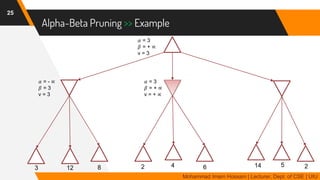
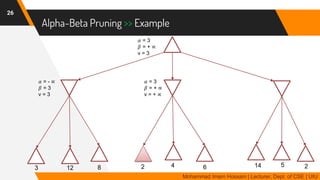
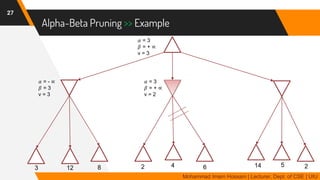
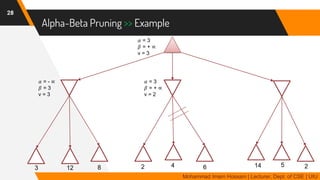
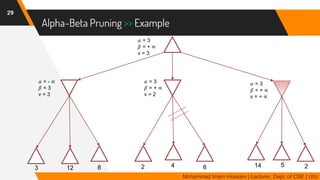
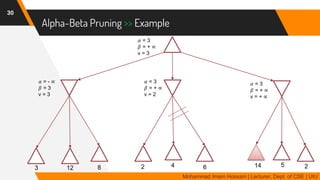
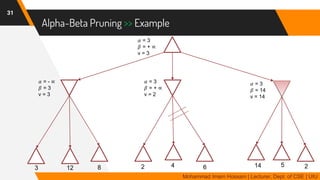
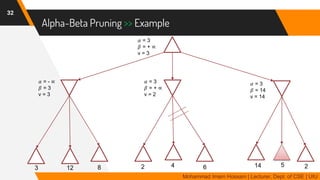
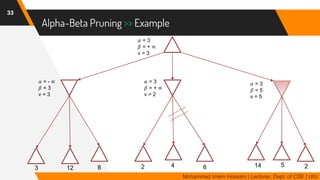
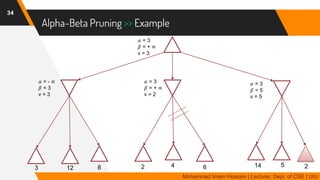
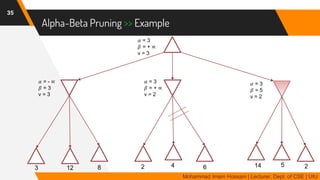
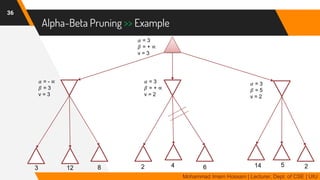
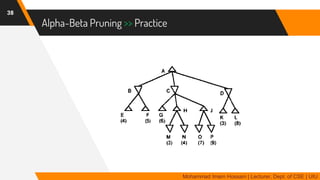
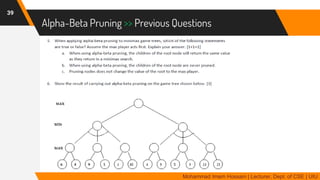
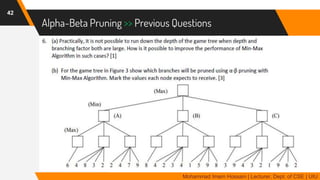
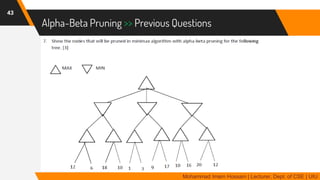
The document discusses adversarial search in multi-agent environments, highlighting competitive and cooperative scenarios where agents' goals may conflict. It covers essential concepts such as game theory, minimax algorithms, game tree complexity, and alpha-beta pruning, emphasizing the need for optimal strategies against unpredictable opponents. Additionally, the document outlines the formal definition of games and the significance of utility functions in determining outcomes.
More Related Content
Similar to AI 6 | Adversarial Search
AI 6 | Adversarial Search
- 1. Adversarial Search CSI 341Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 2. Multi-agent Environment ▸Each agentneeds to consider the actions of other agents and how they affect it’s own welfare. ▸The unpredictability of these other agents can introduce contingencies into the agent’s problem-solving process. ▸Two types: ▹Competitive : When agent B is trying to do something that maximizes its performance measure and minimizes other agent A’s performance measure. For example, playing chess. ▹Cooperative: When both agents are trying to do something that maximizes both agents performance measures. For example, taxi-driving agents. 2 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 3. Adversarial Search ▸Adversarial Search -In this search problem, agents’ goals are in conflict creating a competitive environment. - It is a search when there is an enemy or opponent changing the state of the problem every step in a direction you do not want. - Examples, Chess, Tic-tac-toe, 4 in a row, Checkers, Go, Othello etc. ▸AI Game Theory - Deterministic - Turn taking - Two player - Zero-sum game = It describes a situation in which a participant’s gains or losses is exactly balanced by the losses or gains of the other. - Perfect information - Agents are restricted to a small number of actions described by rules 3 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 4. Games vs. SearchProblems ▸Unpredictable opponent - Specify a move for every possible opponent reply (contingency strategy) - Optimal strategy: the one that leads to outcomes at least as good as any other strategy when one is playing against an infallible opponent. ▸Time limits - Ability to make some decisions even when calculating the optimal decision is infeasible. ▸Terminology: - Two players called MAX and MIN - MAX searches the game tree - MAX moves first and then they take turns moving until the game is over - Ply = one turn taken by one of the players. 4 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 5. Game >> FormalDefinition A game can be formally defined as a kind of search problem with the following elements: ▸S0 : The initial state, which specifies how the game is set up at the start. ▸PLAYER(s) : Defines which player has the move in a state. ▸ACTIONS(s) : Returns the set of legal moves in a state. ▸RESULT(s, a) : The transition model, which defines the result of a move. ▸TERMINAL-TEST(s) : A terminal test which is true when the game is over and false otherwise. States where the game has ended are called terminal states. ▸UTILITY(s, p) : A utility function that defines the final numeric value for a game that ends in terminal state s for a player p. Game Tree >> The initial state, ACTIONS function, and RESULT function define the game tree for the game. It is a tree where the nodes are game states and the edges are moves. Our target is to find the Optimal Strategy … … 5 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 6. Game Tree (Partial) 6 MohammadImam Hossain | Lecturer, Dept. of CSE | UIU
- 7. Game Complexity State-space complexity: -number of legal game positions reachable from the initial position of the game - an upper bound can often be computed by including illegal positions - For example, TicTacToe has 39 = 19683 game states (legal + illegal) Game tree size: - total number of possible games that can be played - number of leaf nodes in the game tree rooted at the game’s initial position - For example, TicTacToe game tree has 9! = 362880 possible games. 7 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 8. Game Complexity Even asimple game like tic-tac-toe is too complex for us to draw the entire game tree on one page, so we will switch to the trivial game as shown below: 8 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 9. MINIMAX Value ▸Given agame tree, the optimal strategy can be determined from the minimax value of each node, which we write as MINIMAX(n) ▸The minimax value of a node is the utility(for MAX) of being in the corresponding state, assuming that both players play optimally from there to the end of the game. ▸The minimax value of a terminal state is just its utility. ▸MAX prefers to move to a state of maximum value, whereas MIN prefers a state of minimum value. 9 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 10. Partial Game Treefor Tic-Tac-Toe 10 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 11. MINIMAX Algorithm 11 Mohammad ImamHossain | Lecturer, Dept. of CSE | UIU
- 12. MINIMAX Algorithm Properties ▸Optimalplay for MAX assumes that MIN also plays optimally, what if MIN doesn’t play optimally? - then it is easy for MAX to do better ▸Complete DFS search? – YES ▸Time Complexity – O(bm) ▸Space Complexity – O(bm) 12 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 13. Multiplayer Games >>Optimal Decision ▸Each node is associated with a vector of values <vA, vB, vC> where each component represents the utility of the state from each player’s viewpoint. ▸Here each player wants to maximize his utility value. 13 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 14. Alpha-Beta Pruning ▸In MINIMAXsearch, the number of game states it has to examine is exponential in the depth of the tree. Unfortunately, we can’t eliminate the exponent. ▸The trick is that it is possible to compute the correct minimax decision without at every node in the game tree. ▸We need to prune away branches that can’t possibly influence the final decision called Alpha-Beta pruning. Basic Idea >> ▸Consider a node n somewhere in the tree, such that Player has a choice of moving to that node. ▸If Player has a better choice m either at the parent node of n or at any choice point further up, then n will never be reached in actual play. ▸Once we have found out enough about n to reach this conclusion, we can prune it. Definitions of 𝜶 and 𝜷 >> ▸Alpha(𝛼) : the value of the best(i.e. highest-value) choice we have found so far at any choice point along the path for MAX ▸Beta(𝛽) : the value of the best(i.e. lowest-value) choice we have found so far at any choice point along the path for MIN 14 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 15. Alpha-Beta Pruning >>Example 15 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642
- 16. Alpha-Beta Pruning >>Example 16 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝
- 17. Alpha-Beta Pruning >>Example 17 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝ 𝛼 = - ∝ 𝛽 = + ∝ v = + ∝
- 18. Alpha-Beta Pruning >>Example 18 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝ 𝛼 = - ∝ 𝛽 = + ∝ v = + ∝
- 19. Alpha-Beta Pruning >>Example 19 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝ 𝛼 = - ∝ 𝛽 = 3 v = 3
- 20. Alpha-Beta Pruning >>Example 20 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝ 𝛼 = - ∝ 𝛽 = 3 v = 3
- 21. Alpha-Beta Pruning >>Example 21 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝ 𝛼 = - ∝ 𝛽 = 3 v = 3
- 22. Alpha-Beta Pruning >>Example 22 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝ 𝛼 = - ∝ 𝛽 = 3 v = 3
- 23. Alpha-Beta Pruning >>Example 23 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = - ∝ 𝛽 = + ∝ v = - ∝ 𝛼 = - ∝ 𝛽 = 3 v = 3
- 24. Alpha-Beta Pruning >>Example 24 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3
- 25. Alpha-Beta Pruning >>Example 25 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = + ∝
- 26. Alpha-Beta Pruning >>Example 26 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = + ∝
- 27. Alpha-Beta Pruning >>Example 27 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2
- 28. Alpha-Beta Pruning >>Example 28 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2
- 29. Alpha-Beta Pruning >>Example 29 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = + ∝ v = + ∝
- 30. Alpha-Beta Pruning >>Example 30 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = + ∝ v = + ∝
- 31. Alpha-Beta Pruning >>Example 31 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = 14 v = 14
- 32. Alpha-Beta Pruning >>Example 32 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = 14 v = 14
- 33. Alpha-Beta Pruning >>Example 33 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = 5 v = 5
- 34. Alpha-Beta Pruning >>Example 34 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = 5 v = 5
- 35. Alpha-Beta Pruning >>Example 35 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = 5 v = 2
- 36. Alpha-Beta Pruning >>Example 36 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU 3 12 8 2514642 𝛼 = 3 𝛽 = + ∝ v = 3 𝛼 = - ∝ 𝛽 = 3 v = 3 𝛼 = 3 𝛽 = + ∝ v = 2 𝛼 = 3 𝛽 = 5 v = 2
- 37. Alpha-Beta Pruning >>Algorithm 37 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 38. Alpha-Beta Pruning >>Practice 38 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 39. Alpha-Beta Pruning >>Previous Questions 39 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 40. Alpha-Beta Pruning >>Previous Questions 40 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 41. Alpha-Beta Pruning >>Previous Questions 41 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 42. Alpha-Beta Pruning >>Previous Questions 42 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 43. Alpha-Beta Pruning >>Previous Questions 43 Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
- 44. 44 THANKS! Any questions? You canfind me at imam@cse.uiu.ac.bd