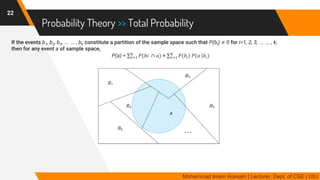
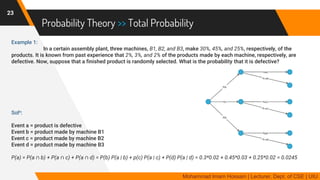
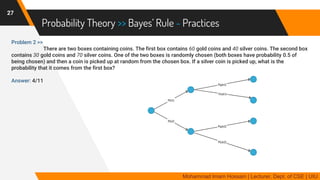
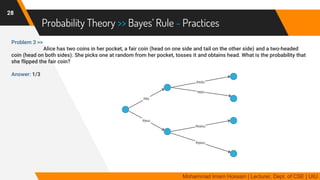
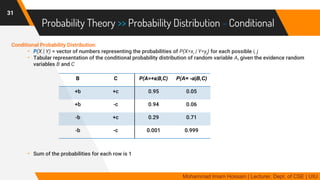
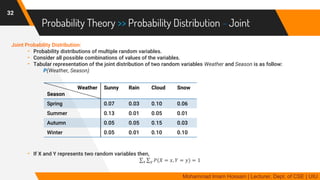
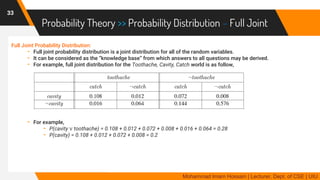
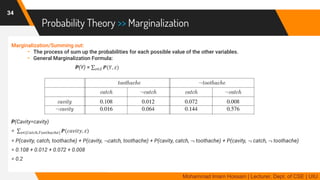
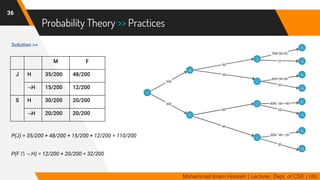
The document discusses methods for quantifying uncertainty in decision-making and diagnosis, focusing on agents that handle uncertainty from partial observability and nondeterminism. It highlights the complexities involved in diagnosis problems, such as laziness and ignorance, and introduces concepts from probability theory and decision theory. Various examples illustrate key ideas such as prior and posterior probabilities, conditional probabilities, and rules for independent and mutually exclusive events.