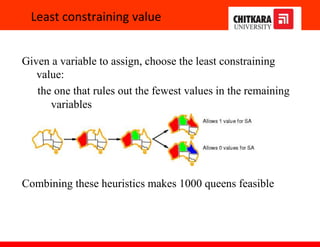
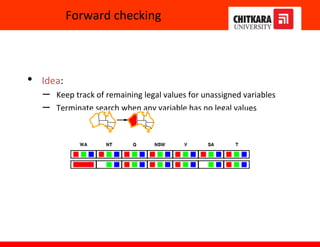
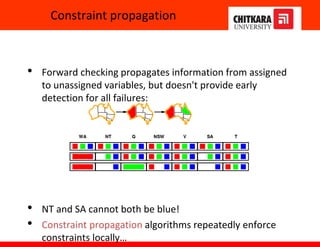
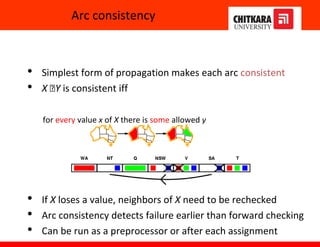
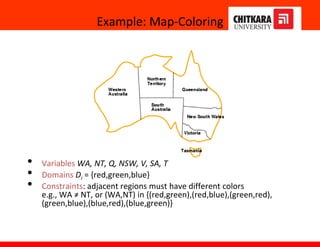
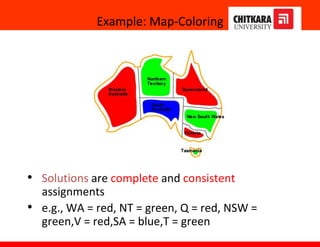
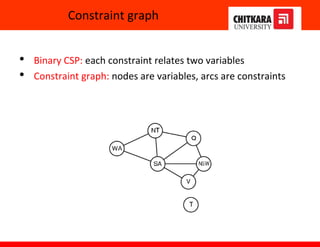
The document discusses constraint satisfaction problems and constraint propagation techniques for solving such problems. It defines constraint satisfaction as solving a problem under certain constraints or rules, where the values assigned to variables must satisfy those constraints. It describes the three main components of a constraint satisfaction problem as the set of variables, their domains, and the constraints. It then discusses solving constraint satisfaction problems using techniques like backtracking search and constraint propagation methods like arc consistency and k-consistency to reduce the search space.

1. Artificial Intelligence
Constraint Satisfaction Problems,
Constraint Propagation, Backtracking
Search.
Prepared by: Ms. Shilpi Singhal

2. Constraint satisfaction
constraint satisfaction means solving a problem under certain
constraints or rules.
Constraint satisfaction is a technique where a problem is solved when
its values satisfy certain constraints or rules of the problem. Such
type of technique leads to a deeper understanding of the problem
structure as well as its complexity.
Constraint satisfaction depends on three components, namely:
X: It is a set of variables.
D: It is a set of domains where the variables reside. There is a specific
domain for each variable.
C: It is a set of constraints which are followed by the set of variables.

3. Constraint satisfaction
In constraint satisfaction, domains are the spaces where the
variables reside, following the problem specific
constraints. These are the three main elements of a
constraint satisfaction technique.
The constraint value consists of a pair of {scope, rel}.
The scope is a tuple of variables which participate in the
constraint and rel is a relation which includes a list of
values which the variables can take to satisfy the
constraints of the problem.

4. Constraint satisfaction
Solving Constraint Satisfaction Problems
The requirements to solve a constraint satisfaction problem (CSP) is:
A state-space
The notion of the solution.
A state in state-space is defined by assigning values to some or all variables such as
{X1=v1, X2=v2, and so on…}.
An assignment of values to a variable can be done in three ways:
Consistent or Legal Assignment: An assignment which does not violate any
constraint or rule is called Consistent or legal assignment.
Complete Assignment: An assignment where every variable is assigned with a value,
and the solution to the CSP remains consistent. Such assignment is known as
Complete assignment.
Partial Assignment: An assignment which assigns values to some of the variables
only. Such type of assignments are called Partial assignments.

5. Constraint satisfaction
A value x2 will contain a value which lies between x1 and x3.
Global Constraints: It is the constraint type which involves an
arbitrary number of variables.
Some special types of solution algorithms are used to solve the
following types of constraints:
Linear Constraints: These type of constraints are commonly used in
linear programming where each variable containing an integer
value exists in linear form only.
Non-linear Constraints: These type of constraints are used in non-
linear programming where each variable (an integer value) exists in
a non-linear form.
Note: A special constraint which works in real-world is known
as Preference constraint.

6. Example: Map-Coloring
• Variables WA, NT, Q, NSW, V, SA, T
• Domains Di = {red,green,blue}
• Constraints: adjacent regions must have different colors
e.g., WA ≠ NT, or (WA,NT) in {(red,green),(red,blue),(green,red),
(green,blue),(blue,red),(blue,green)}

7. Example: Map-Coloring
• Solutions are complete and consistent
assignments
• e.g., WA = red, NT = green, Q = red, NSW =
green,V = red,SA = blue,T = green

8. Constraint graph
• Binary CSP: each constraint relates two variables
• Constraint graph: nodes are variables, arcs are constraints

9. Varieties of CSPs
• Discrete variables
– finite domains:
• n variables, domain size d 🡪 O(dn) complete assignments
• e.g., Boolean CSPs, incl. Boolean satisfiability (NP-complete)
– infinite domains:
• integers, strings, etc.
• e.g., job scheduling, variables are start/end days for each job
• need a constraint language, e.g., StartJob1 + 5 ≤ StartJob3
• Continuous variables
– e.g., start/end times for Hubble Space Telescope observations
– linear constraints solvable in polynomial time by LP

10. Varieties of constraints
• Unary constraints involve a single variable,
– e.g., SA ≠ green
• Binary constraints involve pairs of variables,
– e.g., SA ≠ WA
• Higher-order constraints involve 3 or more
variables,
– e.g., cryptarithmetic column constraints

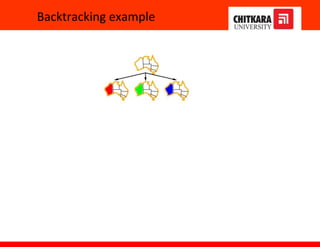
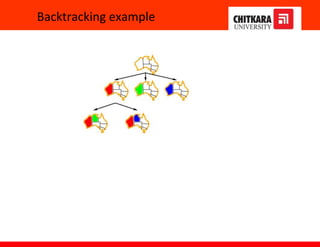
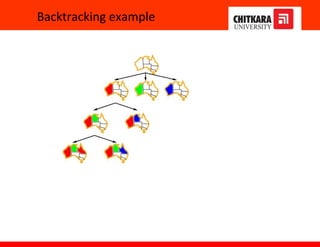
11. Backtracking search
Variable assignments are commutative, i.e.,
[ WA = red then NT = green ] same as [ NT = green then WA = red ]
=> Only need to consider assignments to a single variable at each node
Depth-first search for CSPs with single-variable assignments is called
backtracking search
Can solve n-queens for n ≈ 25

12. Backtracking search

13. Backtracking example

14. Backtracking example

15. Backtracking example

16. Backtracking example

17. Improving backtracking
efficiency
General-purpose methods can give huge gains in
speed:
Which variable should be assigned next?
In what order should its values be tried?
Can we detect inevitable failure early?

18. Most constrained variable
Most constrained variable:
choose the variable with the fewest legal values
a.k.a. minimum remaining values (MRV)
heuristic

19. Most constraining variable
A good idea is to use it as a tie-breaker among most
constrained variables
Most constraining variable:
choose the variable with the most constraints on
remaining variables

20. Least constraining value
Given a variable to assign, choose the least constraining
value:
the one that rules out the fewest values in the remaining
variables
Combining these heuristics makes 1000 queens feasible

21. Forward checking
• Idea:
– Keep track of remaining legal values for unassigned variables
– Terminate search when any variable has no legal values

22. Forward checking
• Idea:
– Keep track of remaining legal values for unassigned variables
– Terminate search when any variable has no legal values

23. Forward checking
• Idea:
– Keep track of remaining legal values for unassigned variables
– Terminate search when any variable has no legal values

24. Forward checking
• Idea:
– Keep track of remaining legal values for unassigned variables
– Terminate search when any variable has no legal values

25. Forward checking
• Idea:
– Keep track of remaining legal values for unassigned variables
– Terminate search when any variable has no legal values

26. Constraint Propagation
In local state-spaces, the choice is only one, i.e., to search for a
solution. But in CSP, we have two choices either:
We can search for a solution or
We can perform a special type of inference called constraint
propagation.
Constraint propagation is a special type of inference which helps in
reducing the legal number of values for the variables. The idea
behind constraint propagation is local consistency.
In local consistency, variables are treated as nodes, and each binary
constraint is treated as an arc in the given problem.

27. Constraint Propagation
There are following local consistencies which are discussed below:
Node Consistency: A single variable is said to be node consistent if all
the values in the variable’s domain satisfy the unary constraints on
the variables.
Arc Consistency: A variable is arc consistent if every value in its
domain satisfies the binary constraints of the variables.
Path Consistency: When the evaluation of a set of two variable with
respect to a third variable can be extended over another variable,
satisfying all the binary constraints. It is similar to arc consistency.
k-consistency: This type of consistency is used to define the notion of
stronger forms of propagation. Here, we examine the k-consistency
of the variables.

28. Constraint propagation
• Forward checking propagates information from assigned
to unassigned variables, but doesn't provide early
detection for all failures:
• NT and SA cannot both be blue!
• Constraint propagation algorithms repeatedly enforce
constraints locally…

29. Arc consistency
• Simplest form of propagation makes each arc consistent
• X 🡪Y is consistent iff
for every value x of X there is some allowed y

30. Arc consistency
• Simplest form of propagation makes each arc consistent
• X 🡪Y is consistent iff
for every value x of X there is some allowed y

31. Arc consistency
• Simplest form of propagation makes each arc consistent
• X 🡪Y is consistent iff
for every value x of X there is some allowed y
• If X loses a value, neighbors of X need to be rechecked

32. Arc consistency
• Simplest form of propagation makes each arc consistent
• X 🡪Y is consistent iff
for every value x of X there is some allowed y
• If X loses a value, neighbors of X need to be rechecked
• Arc consistency detects failure earlier than forward checking
• Can be run as a preprocessor or after each assignment

33. Arc consistency algorithm AC-3
• Time complexity: O(#constraints|domain|3)
Checking consistency of an arc is O(|domain|2)

34. k-consistency
• A CSP is k-consistent if, for any set of k-1 variables, and for any consistent
assignment to those variables, a consistent value can always be assigned to
any kth variable
• 1-consistency is node consistency
• 2-consistency is arc consistency
• For binary constraint networks, 3-consistency is the same as path
consistency
• Getting k-consistency requires time and space exponential in k
• Strong k-consistency means k’-consistency for all k’ from 1 to k
– Once strong k-consistency for k=#variables has been obtained, solution
can be constructed trivially
• Tradeoff between propagation and branching
• Practitioners usually use 2-consistency and less commonly 3-consistency

35. Thank You